Central limit theorem and log-normal distribution
It is inconvenient to work with samples from a distribution of unknown form. Therefore, researchers often switch to considering the sample mean value and hope that thanks to the central limit theorem, the distribution of the sample means should be approximately normal. They say that if we consider samples of size $n \geq 30$, we can expect practically acceptable convergence to normality thanks to Berry–Esseen theorem. Indeed, this statement is almost valid for many real data sets. However, we can actually expect the applicability of this approach only for light-tailed distributions. In the case of heavy-tailed distributions, converging to normality is so slow, that we cannot imply the normality assumption for the distribution of the sample means. In this post, I provide an illustration of this effect using the log-normal distribution.
Let us conduct the following study:
- Enumerate sample sizes $n = \{ 10, 20, 30, 100, 500, 1000 \}$.
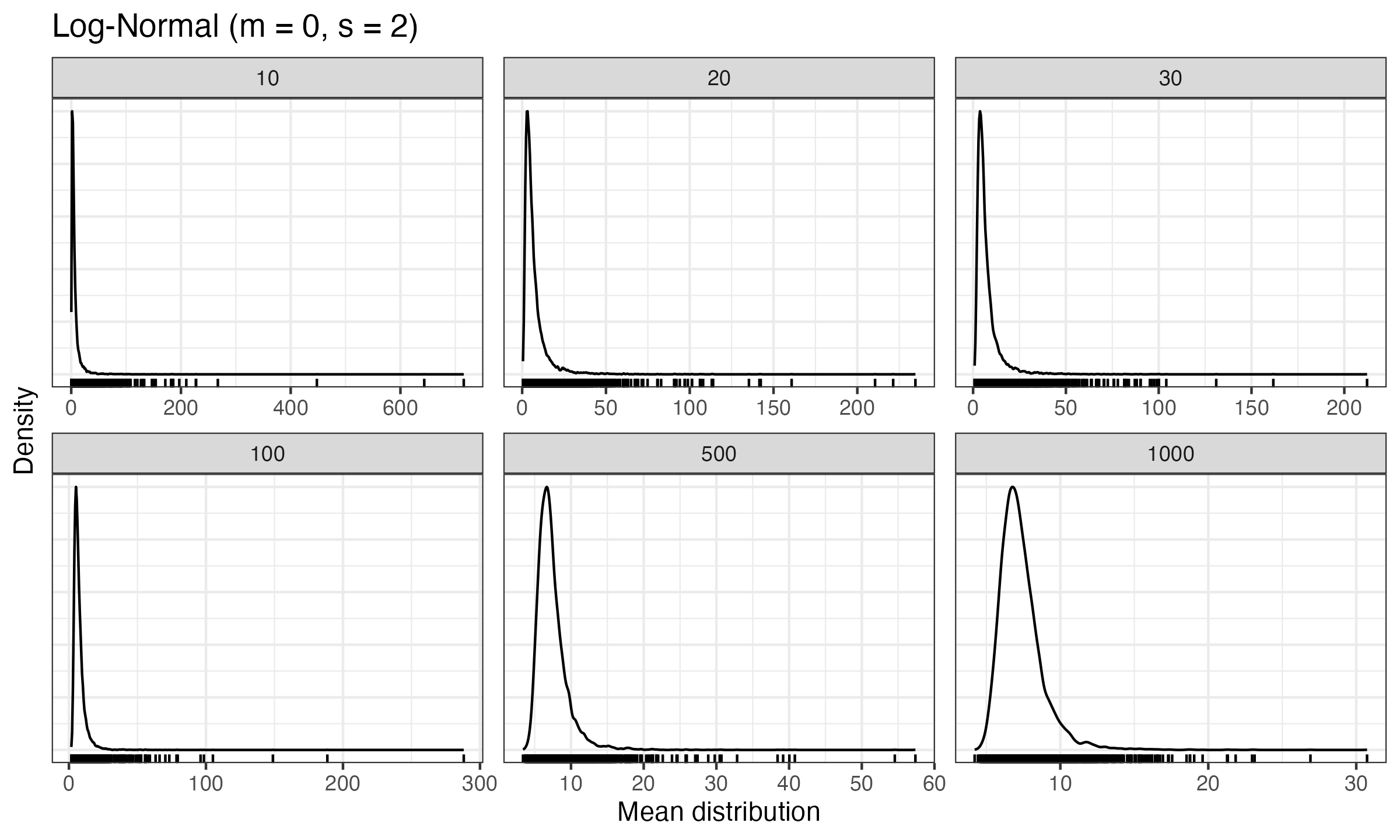
- For each sample size $n$, generate $10\,000$ samples from a log-normal distribution ($\mu = 0$, $\sigma = 2$), calculate the mean of each sample, and draw a density plot of the observed mean values.
Here are the obtained density plots with corresponding rug plots beneath them:
As we can see, we do not visually observe normality not only for $n=30$, but also for $n=1\,000$. Because of the heavy-tailedness of the log-normal distribution, the corresponding sample mean distribution is asymmetric and highly skewed. If we continue to increase $n$, we may expect further convergence to normality. However, in order to achieve a practically acceptable normal approximation, the sample size $n$ is required to be so big that it is often not viable to actually collect samples of such size.