Cohen’s d is a popular way to estimate the effect size between two samples. It works excellent for perfectly normal distributions. Usually, people think that slight deviations from normality shouldn’t produce a noticeable impact on the result. Unfortunately, it’s not always true. In fact, a single outlier value can completely distort the result even in large samples.
In this post, I will present some illustrations for this problem and will show how to fix it.
Cohen’s d
First of all, let’s recall the definition of Cohen’s d. For two samples \(x = \{ x_1, x_2, \ldots, x_n \}\) and \(y = \{ y_1, y_2, \ldots, y_n \}\), the Cohen’s d is defined as follows ([Cohen1988]):
\[d_{xy} = \frac{\overline{y}-\overline{x}}{s_{xy}} \]
where \(s_{xy}\) is the pooled standard deviation:
\[s_{xy} = \sqrt{\frac{(n_x - 1) s^2_x + (n_y - 1) s^2_y}{n_x + n_y - 2}}. \]
There is a rule of thumb that is widely used to interpret Cohen’s d value:
| d | Effect |
|---|---|
| 0.2 | Small |
| 0.5 | Medium |
| 0.8 | Large |
E.g., if \(d_{xy} < 0.2\), we can say that the difference between \(x\) and \(y\) is small. If \(d_{xy} > 0.8\), the difference is large
The problem
Now we are going to discuss a simple example that demonstrates the effect of a single outlier. Let’s consider the two following small samples:
\[x = \{ -1.4,\; -1,\; -0.2,\; 0,\; 0.2,\; 1,\; 1.4 \} \quad \big( \overline{x} = 0,\; s_x = 1 \big), \]
\[y = \{ -0.4,\; 0,\; 0.8,\; 1,\; 1.2,\; 2,\; 2.4 \} \quad \big( \overline{y} = 0,\; s_y = 1 \big). \]
Thus, the Cohen’s d equals \(1\):
\[d_{xy} = \frac{\overline{y}-\overline{x}}{s_{xy}} = \frac{1 - 0}{1} = 1. \]
We can see that \(d_{xy}\) describes a large effect (because it’s larger than 0.8 which is the large effect threshold).
Now let’s replace the last element of \(y\) with a high outlier and build a new sample \(z\):
\[z = \{ -0.4,\; 0,\; 0.8,\; 1,\; 1.2,\; 2,\; 100 \} \quad \big( \overline{z} \approx 14.08,\; s_{z} \approx 37.89 \big). \]
Since the mean value has been significantly increased (\(\overline{z} \approx 14.08 \gg \overline{y} = 0\)), we could expect that the Cohen’s d value should be increased as well. However, we observe an opposite situation because of the increased pooled standard deviation:
\[s_{xz} = \sqrt{\frac{(n_x - 1) s^2_x + (n_z - 1) s^2_z}{n_x + n_z - 2}} = \sqrt{\frac{6\cdot 1^2 + 6\cdot 37.89^2}{12}} \approx 26.8. \]
\[d_{xz} = \frac{\overline{z}-\overline{x}}{s_{xz}} \approx \frac{14.08}{26.8} \approx 0.53. \]
As we can see, this outlier spoiled our conclusion. Now, the Cohen’s d equals 0.53 (medium effect) instead of 1.0 (large effect). Technically, the result is correct (because the standard deviation of \(z\) is huge), but it doesn’t properly describe the actual difference between \(x\) and \(y\).
Here you could say that the size of the considered samples is too small, it’s not enough to get a reasonable Cohen’s d value. OK, let’s see what kind of situation we get on larger samples.
Numerical simulations
Let’s conduct the following simulation:
- Generate random sample \(x = \{x_1, \ldots, x_n \}\) from \(\mathcal{N}(0, 1^2)\).
- Generate random sample \(y = \{y_1, \ldots, y_n \}\) from \(\mathcal{N}(1, 1^2)\) and replace \(y_n\) with \(y_n = 100\).
- Calculate the Cohen’s d value between \(x\) and \(y\).
- Repeat steps previous three steps 1000 times.
- Build a distribution based on 1000 collected Cohen’s d values.
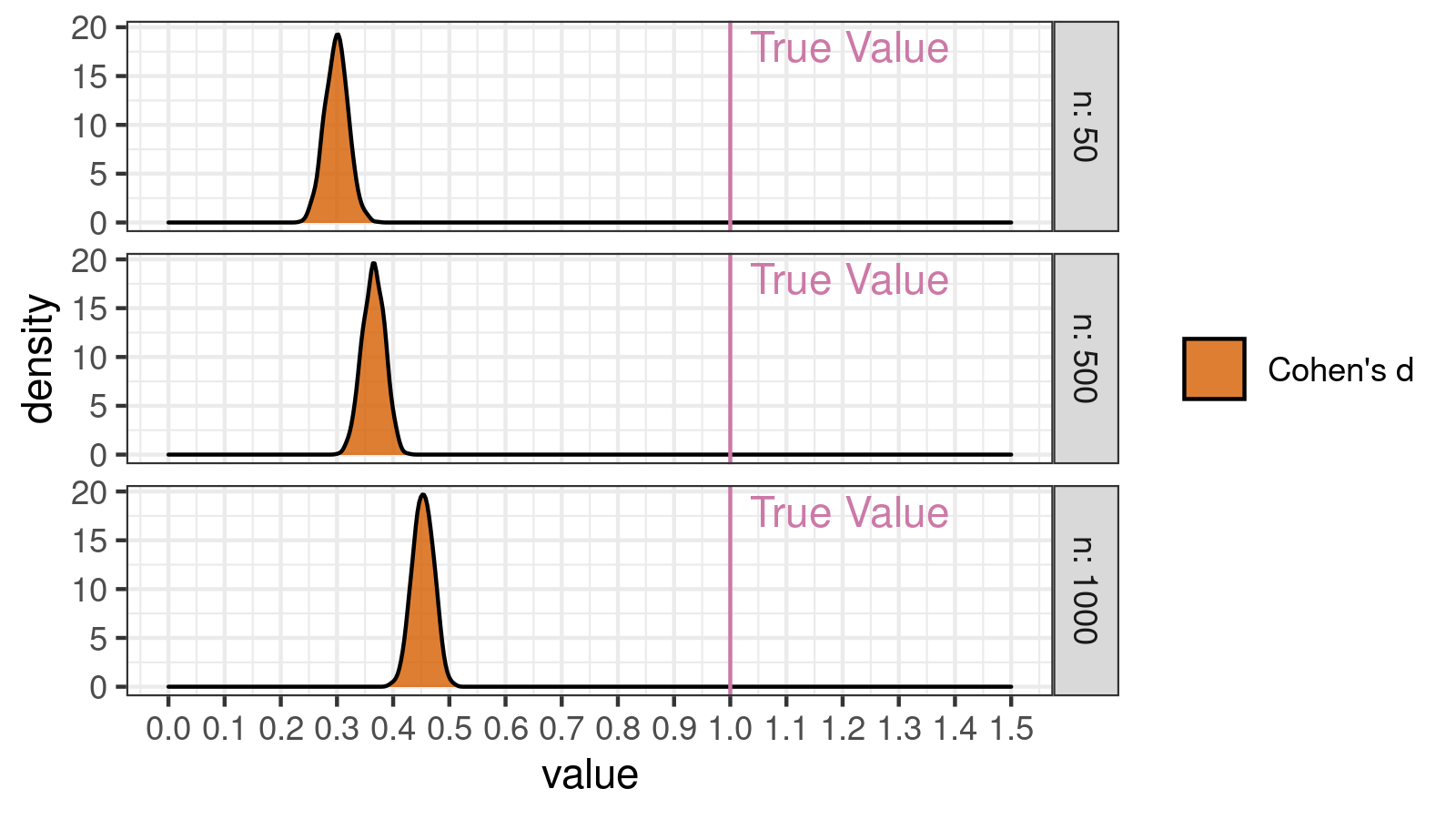
Below you can see corresponding density plots (KDE, normal kernel, Sheather & Jones) for \(n = 50\), \(n = 500\), and \(n = 1000\).
In these simulation, we got the following results:
- \(n=50\): all Cohen’s d values are inside \([0.23; 0.37]\)
- \(n=500\): all Cohen’s d values are inside \([0.30; 0.43]\)
- \(n=1000\): all Cohen’s d values are inside \([0.39; 0.51]\)
As you can see, instead of the expected large effect (\(d = 1\)), we constantly get small or medium effect (\(d < 0.52\)). Even when \(n = 1000\), a single extreme number could completely distort the result.
So, how to solve this problem?
The solution
In one of the previous posts, I described a nonparametric effect size estimator which is consistent with Cohen’s d. Here is a quick definition:
The effect size \(\gamma_p\) can be estimated as follows:
\[\gamma_p = \frac{Q_p(y) - Q_p(x)}{\mathcal{PMAD}_{xy}}, \]
where \(\mathcal{PMAD}_{xy}\) is the pooled median absolute deviation:
\[\mathcal{PMAD}_{xy} = \sqrt{\frac{(n_y - 1) \mathcal{MAD}^2_y + (n_y - 1) \mathcal{MAD}^2_y}{n_x + n_y - 2}}. \]
In this post, we are going to apply it only for the median (we need only \(\gamma_{0.5}\)). In order to improve the accuracy, we use the Harrell-Davis quantile estimator ([Harrell1982]) to estimate the median (\(Q_{0.5}\)) and the median absolute deviation (\(\mathcal{MAD}_x\), \(\mathcal{MAD}_y\)). The consistency constant \(C\) for \(\mathcal{MAD}\) equals \(1.4826\), which makes \(\mathcal{MAD}\) a consistent estimator for the standard deviation estimation.
Thus, in the case of the normal distribution, \(\gamma_p\) could be used as a good approximation of the Cohen’s d. In this case of non-normal distribution, it provides a robust and stable alternative to the Cohen’s d.
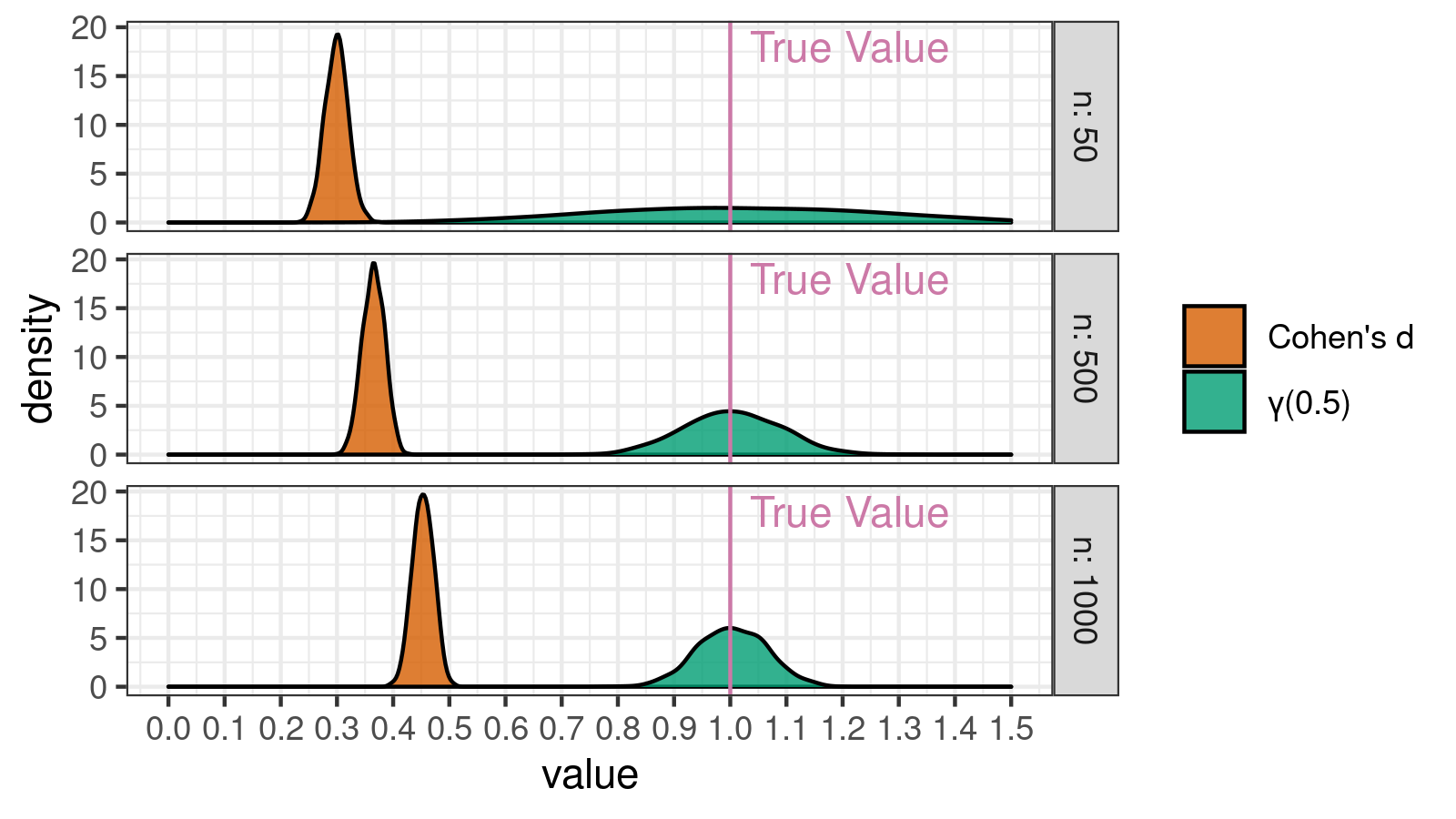
Let’s repeat the above simulation with outliers and build corresponding density plots for \(\gamma_{0.5}\):
As you can see, a single outlier couldn’t spoil the \(\gamma_{0.5}\) values. The obtained effect size values are normally distributed around \(1.0\), which is the true effect size value.
Conclusion
The \(\gamma_p\) effect size is a good alternative for Cohen’s d. For the normal distributions, it works similar to Cohen’s d. \(\gamma_p\) based on two robust metrics (the Harrell-Davis powered medians and median absolution deviations) instead of non-robust metrics in the original Cohen’s d equation (the mean and the standard deviation). Thus \(\gamma_p\) is also robust and works well even when we observe deviations from normality. In the case of non-normal distributions, it allows comparing individual quantiles instead of focusing only on the central tendency like the mean or the median.
References
- [Cohen1988]
Cohen, Jacob. (1988). Statistical Power Analysis for the Behavioral Sciences. New York, NY: Routledge Academic - [Harrell1982]
Harrell, F.E. and Davis, C.E., 1982. “A new distribution-free quantile estimator.” Biometrika, 69(3), pp.635-640.
https://pdfs.semanticscholar.org/1a48/9bb74293753023c5bb6bff8e41e8fe68060f.pdf