Dynamical System Case Study 1 (symmetric 3d system)
Let’s consider the following dynamical system:
$$ \begin{cases} \dot{x}_1 = f(x_3) - x_1,\\ \dot{x}_2 = f(x_1) - x_2,\\ \dot{x}_3 = f(x_2) - x_3, \end{cases} $$where $f(x) = \alpha / (1+x^m)$ is a Hill function. In this case study, we explore the phase portrait of this system for $\alpha = 18,\; m = 3$.
Preparation
First of all, let’s find the stationary point of this system. Since in such point $\dot{x}_1=\dot{x}_2=\dot{x}_3=0$, we have the following equation:
$$ x_1 = f(f(f((x_1)))). $$Since $x_1$ is monotonically increasing and $f(f(f(x_1))))$ is monotonically decreasing, this equation has exactly one solution. It’s easy to see that this solution is $x_0=x_1=x_2=x_3=2$.
Next, we build the corresponding linearization matrix:
$$ M = \begin{bmatrix} -1 & 0 & f'(x_0)\\ f'(x_0) & -1 & 0\\ 0 & f'(x_0) & -1 \end{bmatrix}. $$Since $f'(x) = -\alpha m x^{m - 1} / (x ^ m + 1)^2$, we have:
$$ f'(x_0) = -18 * 3 * 2^2 / (2^3+1)^2 = -216 / 81 = -8/3 \approx -2.66667. $$Thus,
$$ M = \begin{bmatrix} -1 & 0 & -8/3\\ -8/3 & -1 & 0\\ 0 & 8/3 & -1 \end{bmatrix}. $$Now we can get the eigenvalues $\lambda_i$ and eigenvectors $e_i$:
$$ \lambda_1 \approx -3.666667,\quad \lambda_2 \approx 0.333333+2.309401i,\quad \lambda_3 \approx 0.333333-2.309401i, $$$$ \begin{bmatrix} e_1 \\ e_2 \\ e_3 \end{bmatrix} = \begin{bmatrix} -0.5773503, & -0.5773503, & -0.5773503\\ -0.2886751+0.5i, & -0.2886751-0.5i, & 0.5773503\\ -0.2886751-0.5i, & -0.2886751+0.5i, & 0.5773503 \end{bmatrix}. $$The most expressive phase portrait could be obtained using a projection on $(e_2, e_3)$ or $(\Re(e_2), \Im(e_2)) = (\Re(e_3), -\Im(e_3))$.
Phase portraits
In order to explore phase portraits, we perform several simulation studies. In each simulation, we generate several trajectories from random start points and draw three plots:
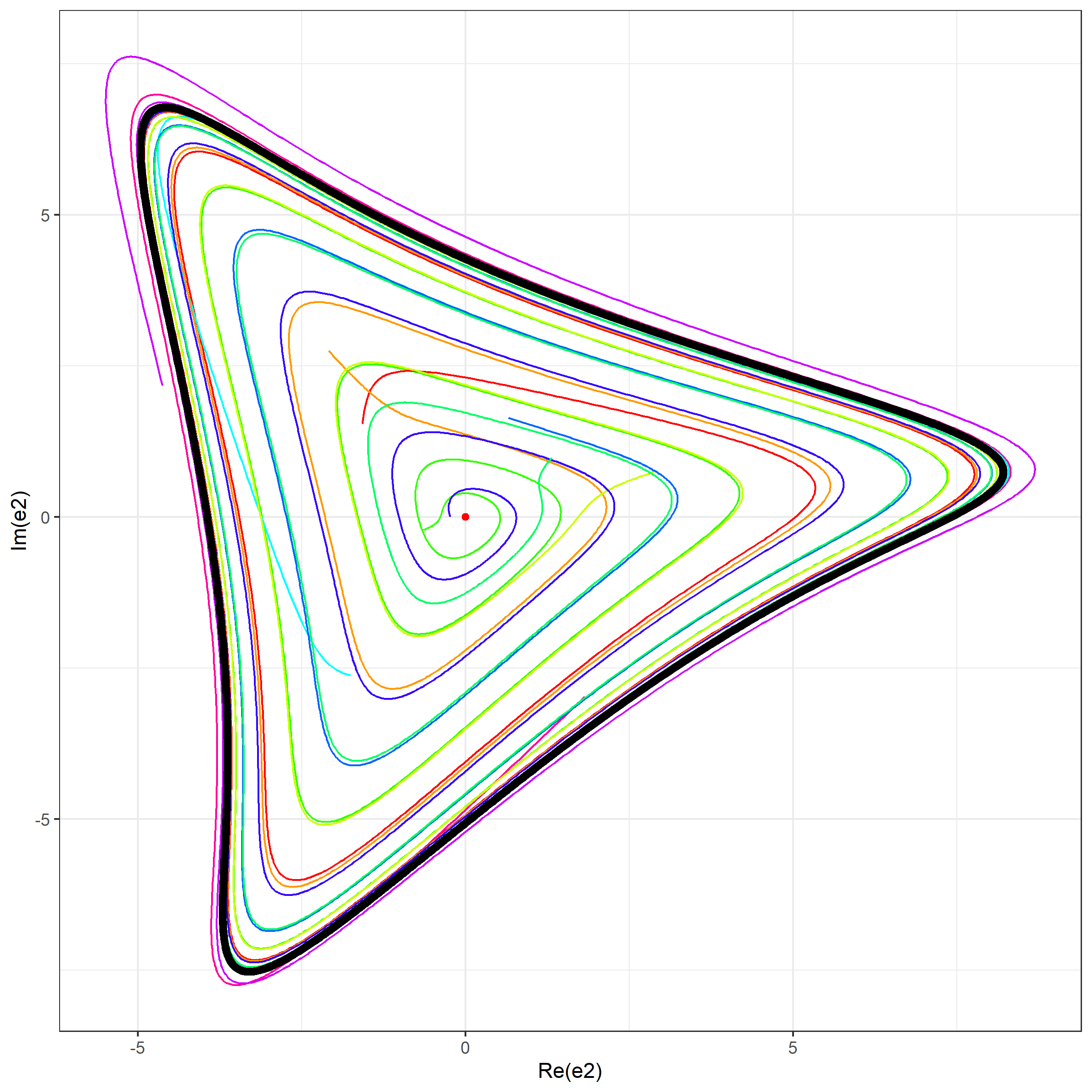
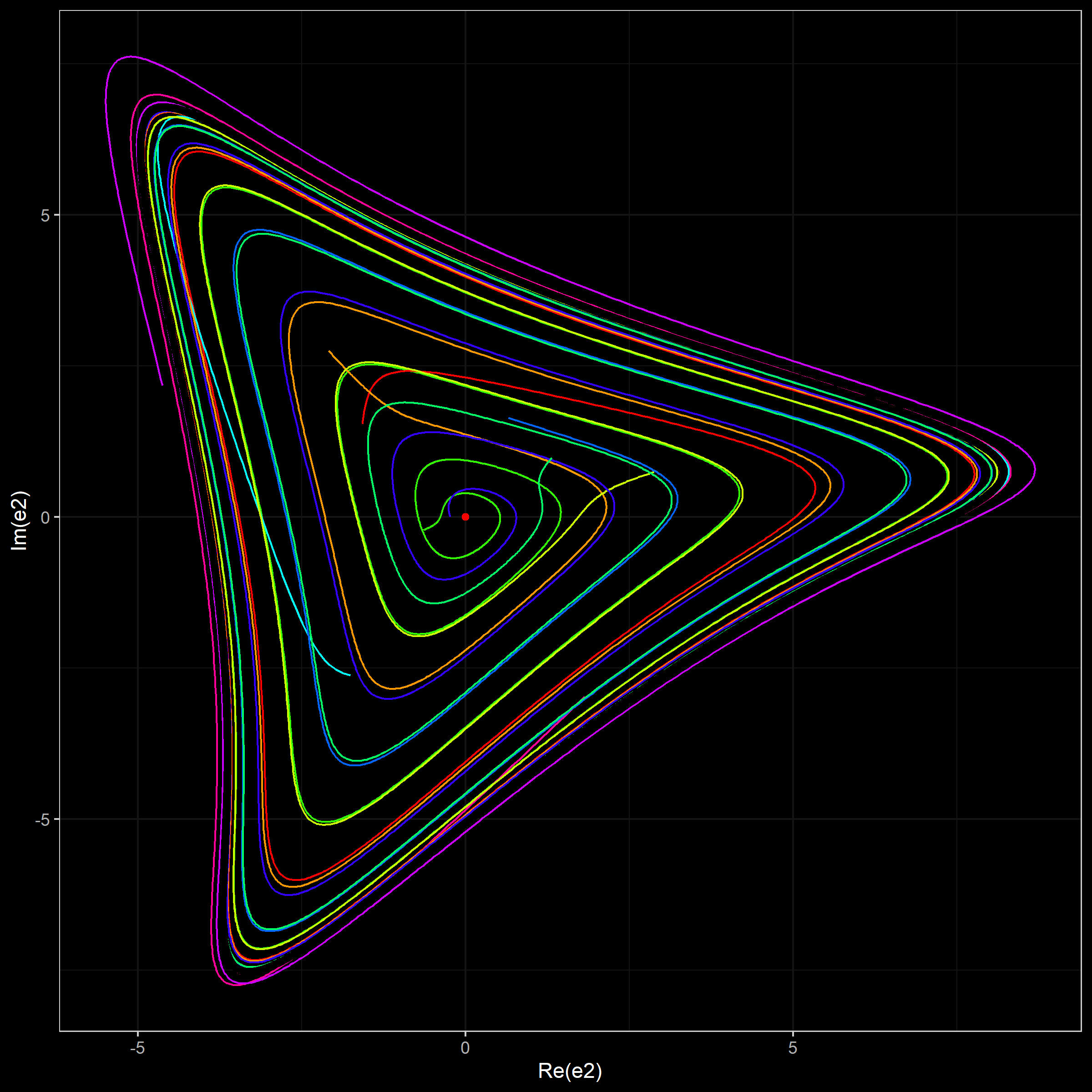
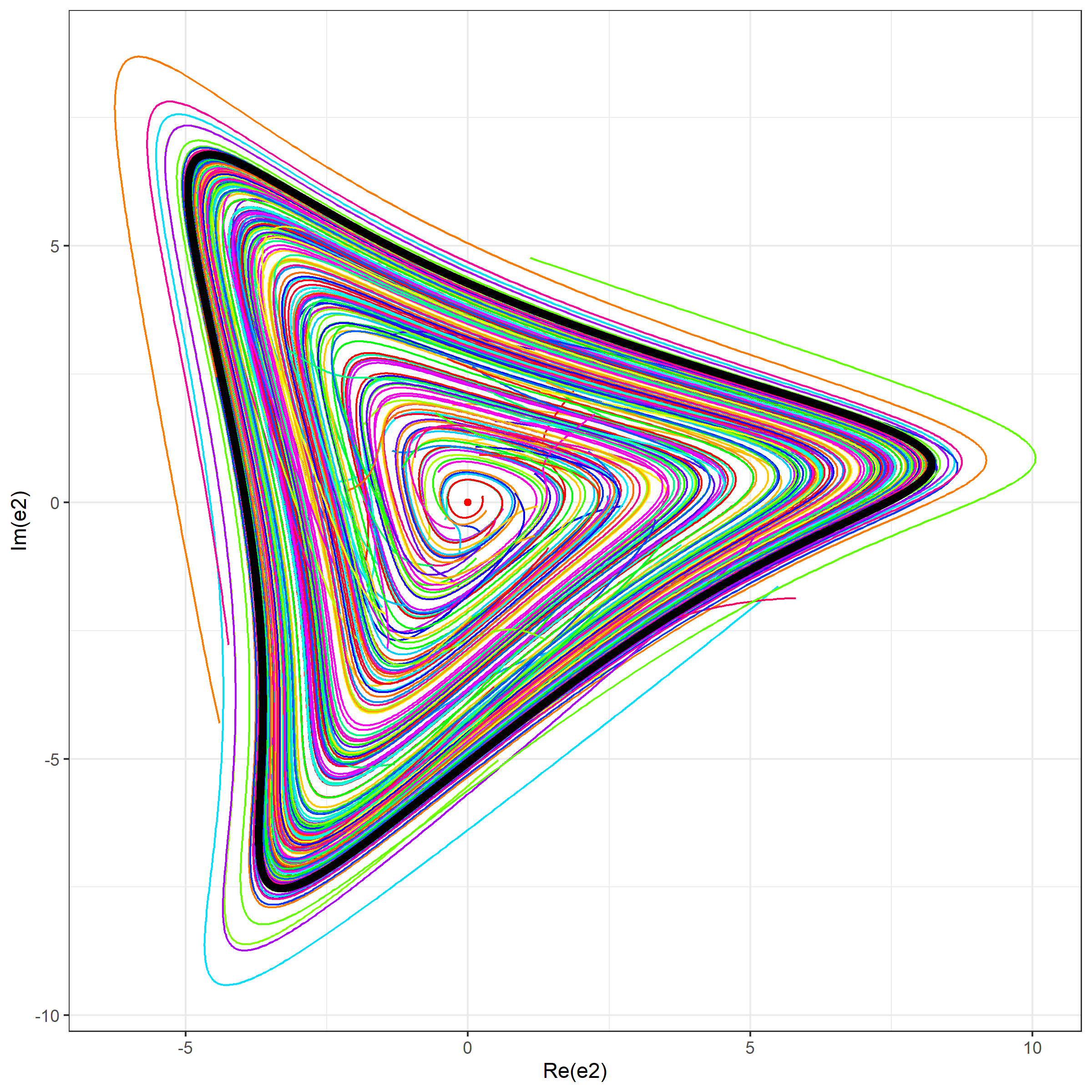
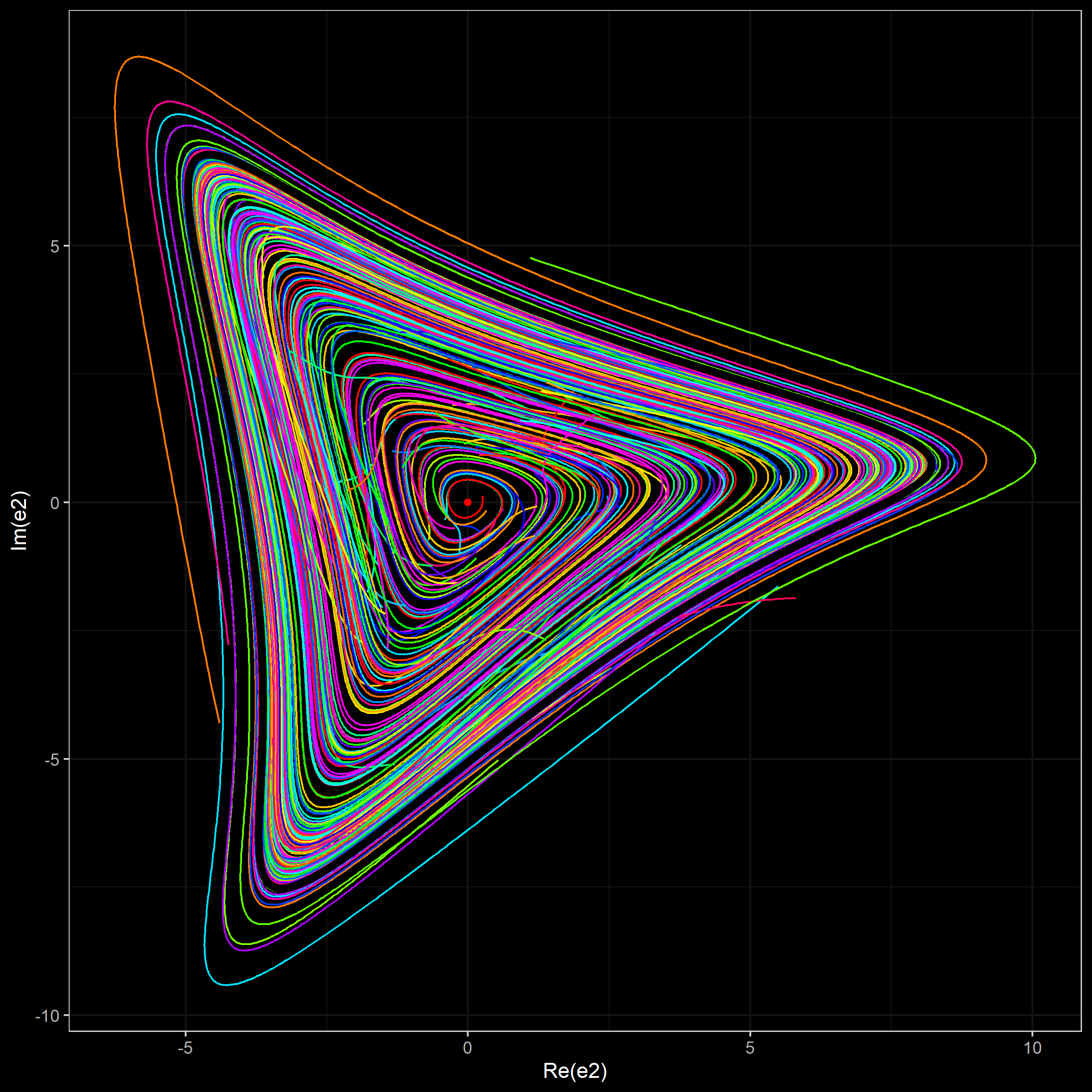
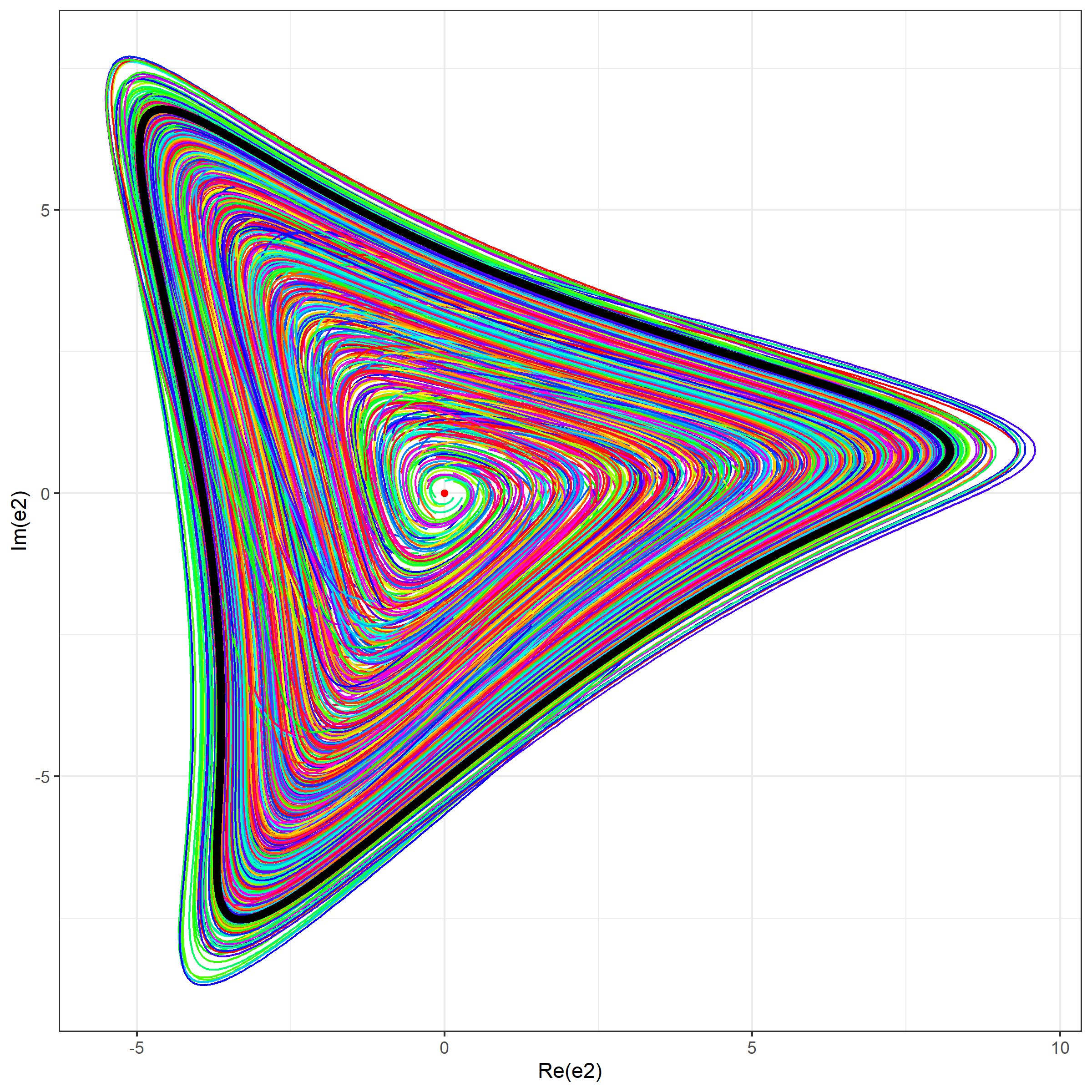
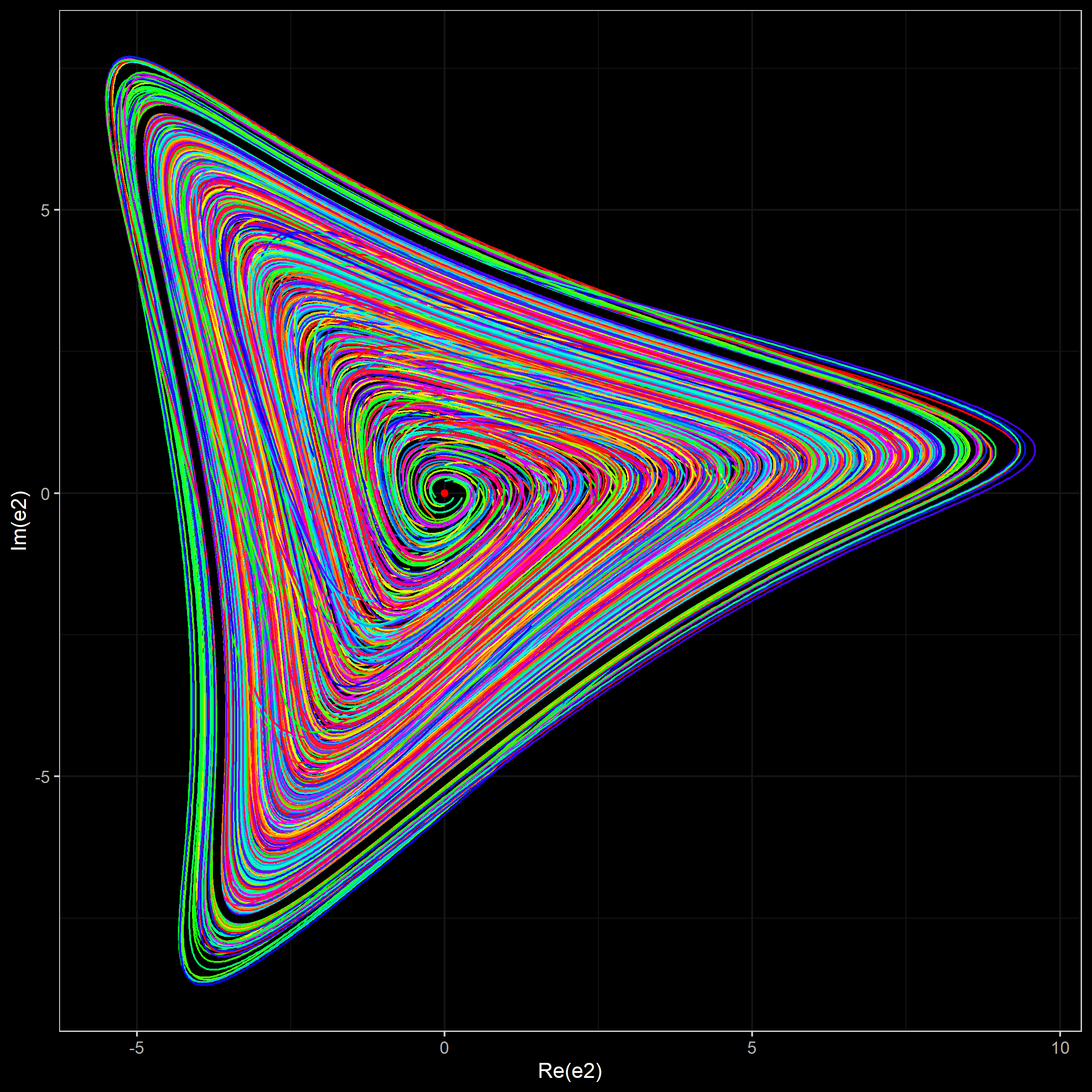
- A projection of simulated trajectories on $(\Re(e_2), \Im(e_2))$. Each trajectory has own color from a rainbow palette. The limit cycle is shown using the black color.
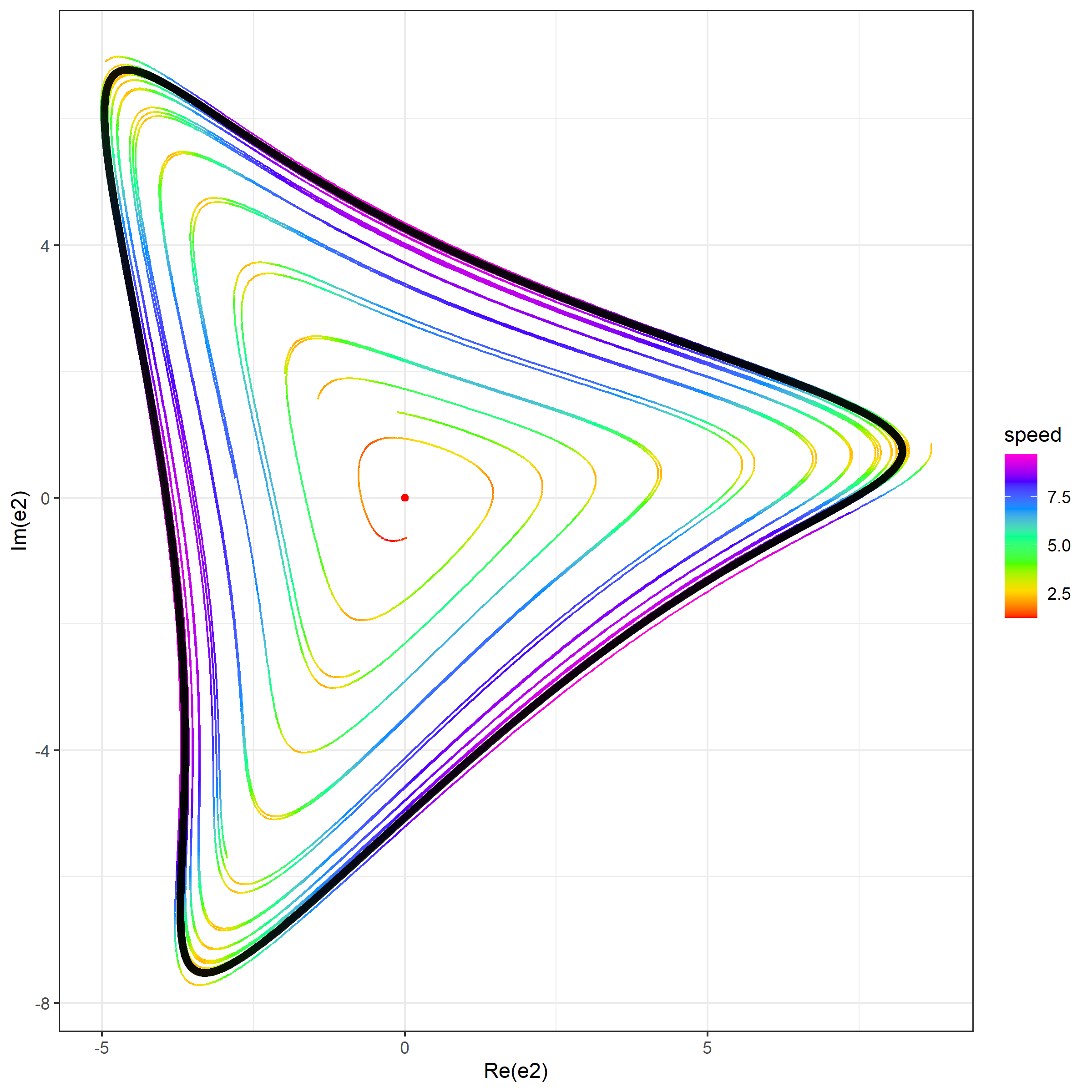
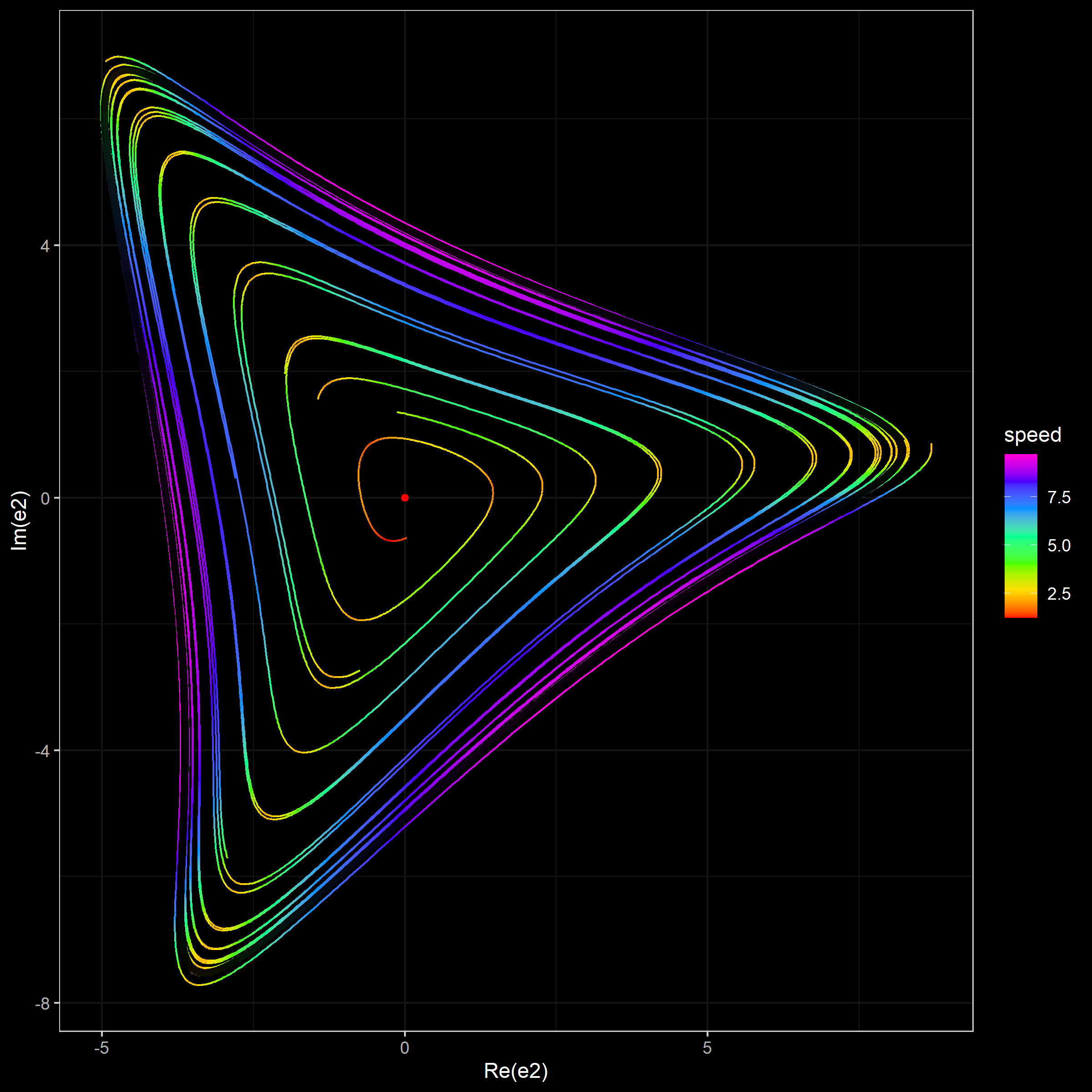
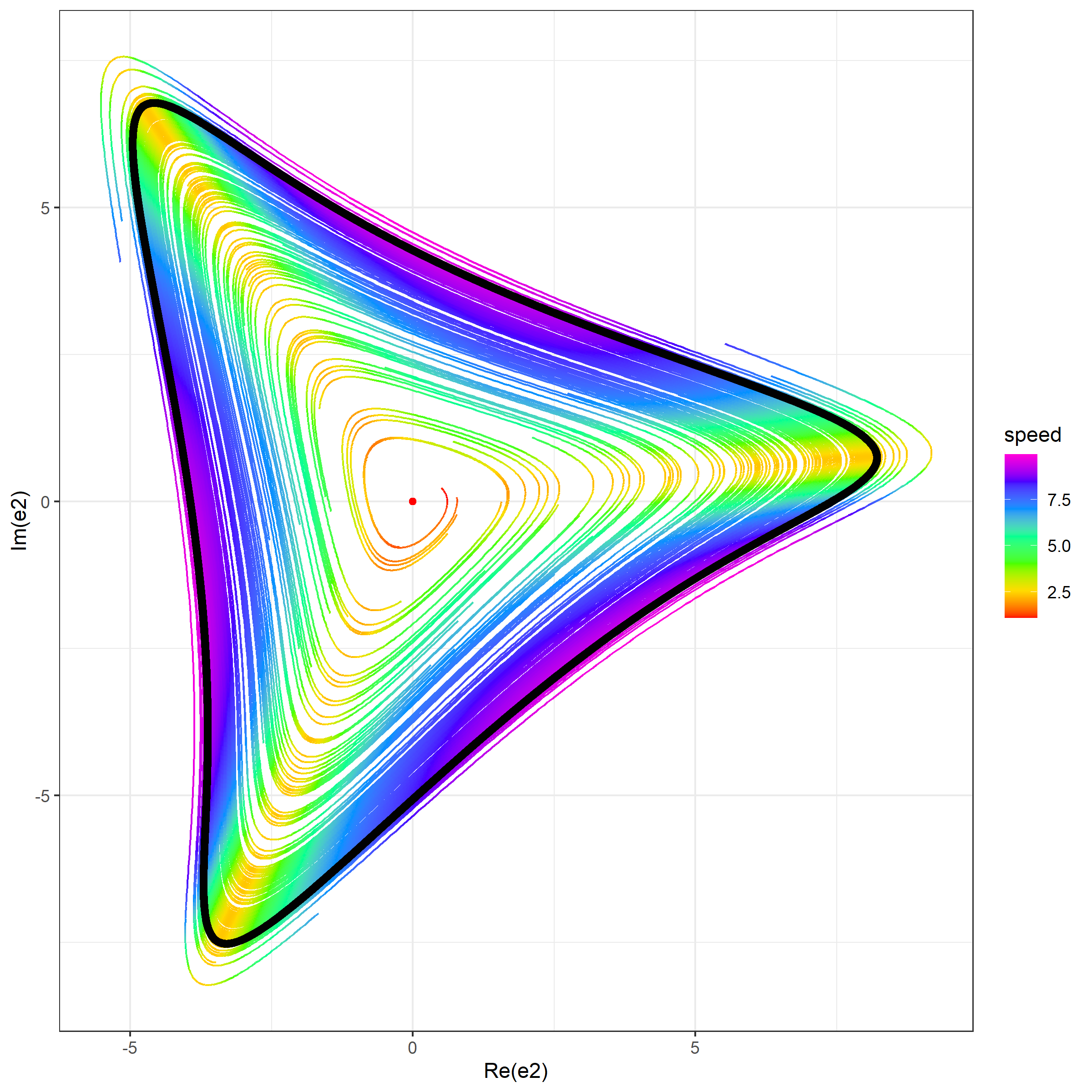
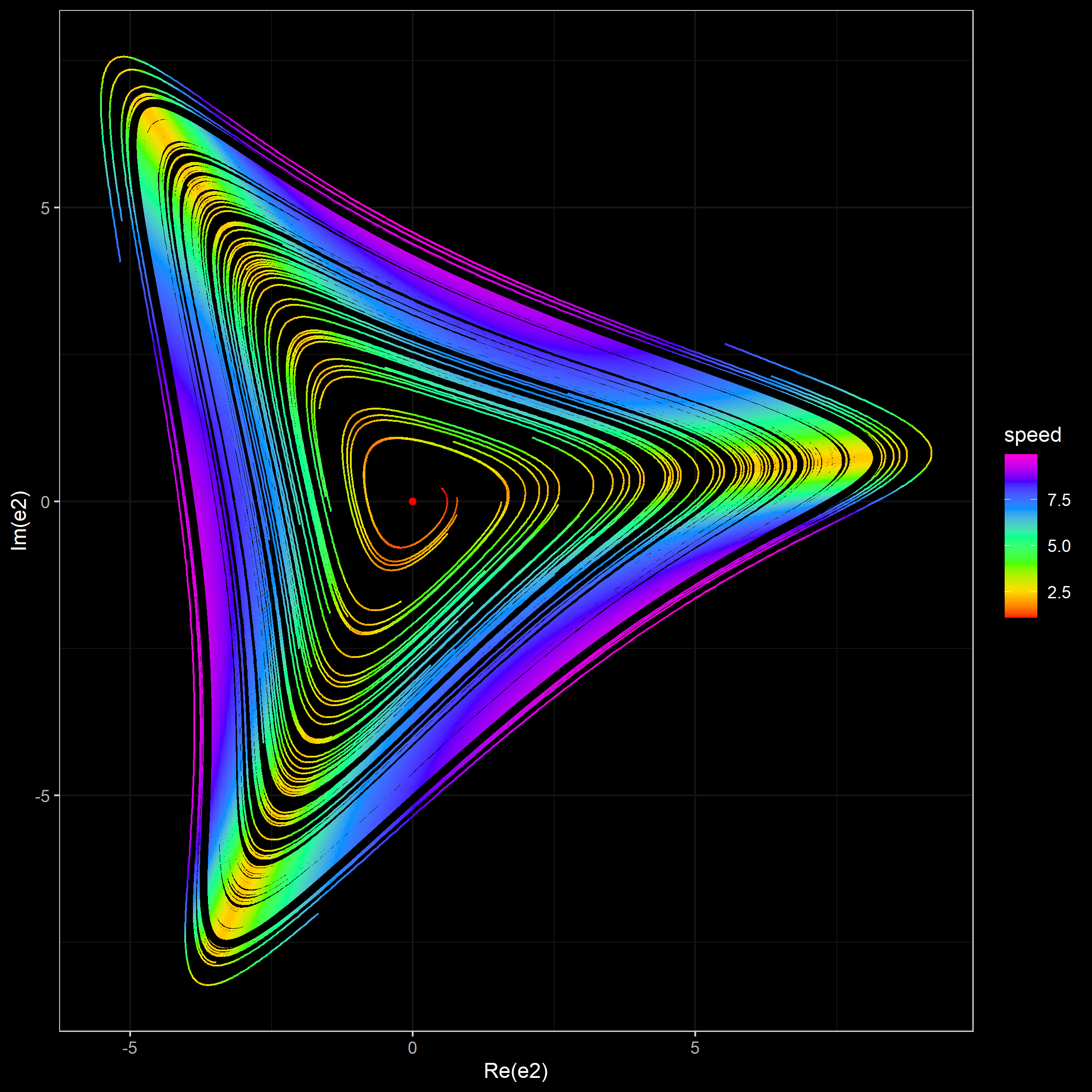
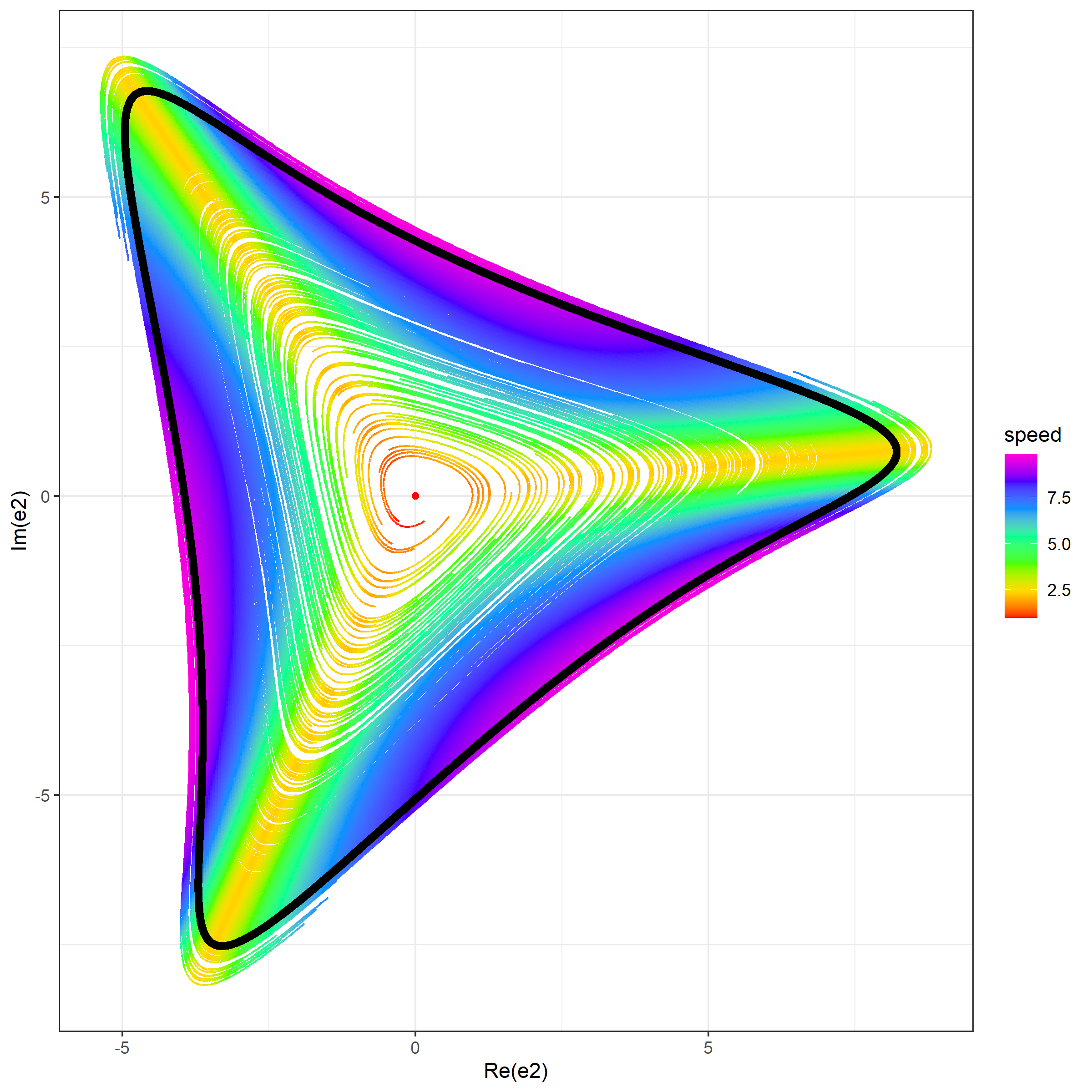
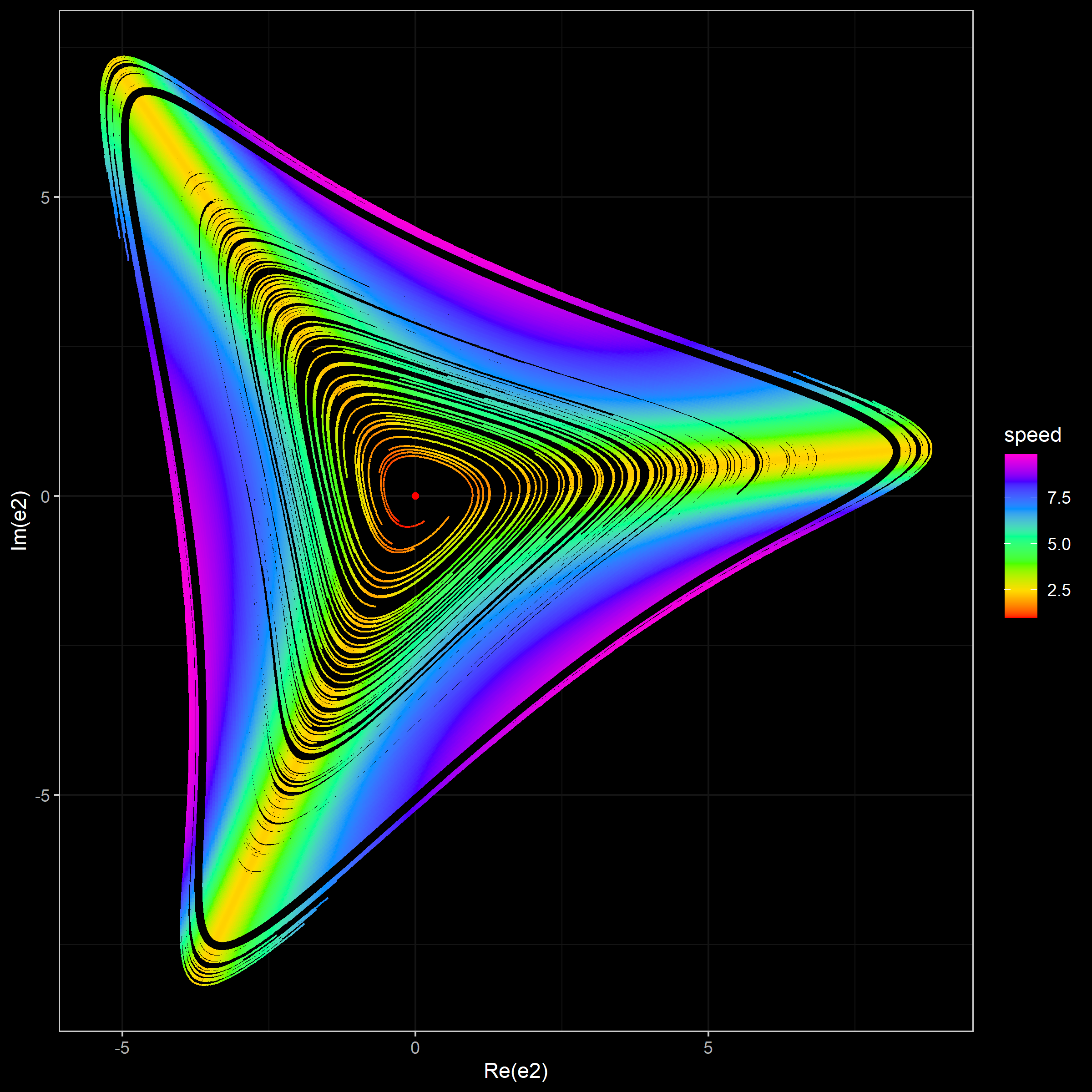
- A projection of simulated trajectories on $(\Re(e_2), \Im(e_2))$. For each trajectory point, the color defines the current speed ($\sqrt{\dot{x}_1^2+\dot{x}_2^2+\dot{x}_3^2}$). The limit cycle is shown using the black color. The beginning of each trajectory is drop in order to provide a more consistent picture.
- A 3D projection of simulation trajectories on $(e1_, \Re(e_2), \Im(e_2))$. These visualizations are heavy, so you should click on “Show 3D plot” in order to explore the plot.
Simulation 1 (10 trajectories)
In this simulation, we generate 10 trajectories from random start points around the stationary point uniformly taken in $(x_1, x_2, x_3)$.
Simulation 2 (100 trajectories)
In this simulation, we generate 100 trajectories from random start points around the stationary point uniformly taken in $(x_1, x_2, x_3)$.
Simulation 3 (500 trajectories)
In this simulation, we generate 500 trajectories from random start points around the stationary point uniformly taken in $(e_1, e_2, e_3)$.
Source code
library(deSolve)
library(ggplot2)
library(dplyr)
library(tidyr)
library(plotly)
simParams <- list(
totalTime = 50,
step = 0.01,
startThreshold = 3,
endThreshold = 45
)
hypot <- function(x, y) sqrt(x^2 + y^2)
fp <- list(a = 18, m = 3)
f <- function(x, a = fp$a, m = fp$m) a / (1 + x ^ m)
df <- function(x, a = fp$a, m = fp$m) -a * m * x ^ (m - 1) / (x ^ m + 1)^2
model <- function(t, x, parms) {
with(as.list(c(parms, x)), {
dx1 <- f(x3) - x1
dx2 <- f(x1) - x2
dx3 <- f(x2) - x3
list(c(dx1, dx2, dx3))
})
}
calc.speed <- function(x) sqrt(sum(unlist(model(0, x, 0))^2))
x0 <- uniroot(function(x) f(f(f(x)))-x, c(0, fp$a), tol = 1e-9)$root
M <- matrix(c(
-1, 0, df(x0),
df(x0), -1, 0,
0, df(x0), -1
), nrow = 3, ncol = 3, byrow = TRUE)
eigenM <- tryCatch(eigen(M), error = function(e) list(values = rep(NA, 6), vectors = matrix(rep(NA, 36), ncol = 6)))
Ml <- eigenM$values
Me <- eigenM$vectors
simulate <- function(name, start) {
times <- seq(0, simParams$totalTime, by = simParams$step)
traj <- data.frame(lsoda(start, times, model, c()))
traj$speed <- sapply(1:nrow(traj), function(index) calc.speed(traj[index, 2:4]))
proj <- function(e){
dotProduct <- rowSums(t(t((traj[,2:4]) - x0) * e))
l <- sqrt(sum(e^2))
dotProduct / l
}
traj$e1 <- proj(Re(Me[,1]))
traj$e2 <- proj(Re(Me[,2]))
traj$e3 <- proj(Im(Me[,2]))
traj$name <- name
traj
}
generate.input <- function(type, maxTraj = -1) {
if (type == 1) {
if (maxTraj <= 0)
maxTraj <- 1
return(data.frame(
x1 = abs(x0 + rnorm(maxTraj) * 3),
x2 = abs(x0 + rnorm(maxTraj) * 3),
x3 = abs(x0 + rnorm(maxTraj) * 3)
))
}
if (type == 2) {
input <- expand.grid(e2 = seq(-5, 8, by = 0.2), e3 = seq(-7.5, 7, by = 0.2))
noise <- runif(nrow(input), -5, 5)
ue1 <- Re(Me[,1])
ue2 <- Re(Me[,2])
ue3 <- Im(Me[,2])
input$x1 <- noise * ue1[1] + input$e2 * ue2[1] + input$e3 * ue3[1]
input$x2 <- noise * ue1[2] + input$e2 * ue2[2] + input$e3 * ue3[2]
input$x3 <- noise * ue1[3] + input$e2 * ue2[3] + input$e3 * ue3[3]
input <- input[input$x1 > 0 & input$x2 > 0 & input$x3 > 0,]
if (maxTraj > 0 & maxTraj < nrow(input))
input <- input[sample(1:nrow(input), maxTraj),]
return(input)
}
stop("Unknown type")
}
simulate2 <- function(input) {
get.input <- function(i) c(x1 = input[i, "x1"], x2 = input[i, "x2"], x3 = input[i, "x3"])
do.call("rbind", lapply(1:nrow(input), function(i) simulate(paste0("t", i), get.input(i))))
}
draw.simple <- function(traj) {
ggplot(traj, aes(e2, e3, col = name)) +
geom_path(aes(group = name)) +
geom_point(aes(x, y), data.frame(x = 0, y = 0), col = "red") +
geom_path(aes(e2, e3, group = name), traj[traj$time > simParams$endThreshold,], col = "black", size = 2, alpha = 0.1) +
scale_color_manual(values = sample(rainbow(length(unique(traj$name))))) +
theme(legend.position="none") +
labs(x = "Re(e2)", y = "Im(e2)")
}
draw.speed <- function(traj) {
ggplot(traj[traj$time > simParams$startThreshold,], aes(e2, e3, col = speed)) +
geom_path(aes(group = name)) +
geom_point(aes(x, y), data.frame(x = 0, y = 0), col = "red") +
geom_path(aes(e2, e3, group = name), traj[traj$time > simParams$endThreshold,], col = "black", size = 2, alpha = 0.1) +
scale_color_gradientn(colours = rainbow(7)) +
labs(x = "Re(e2)", y = "Im(e2)")
}
draw.3d <- function(traj) {
traj3d <- traj[traj$time > simParams$startThreshold,c("time", "e1", "e2", "e3", "name")]
traj3d[,2:4] <- round(traj3d[,2:4], 3) # Compressing
plot_ly(
traj3d, x = ~e1, y = ~e2, z = ~e3,
type = 'scatter3d', mode = 'lines', opacity = 1, color = ~name,
colors = sample(rainbow(length(unique(traj$name))))) %>%
layout(showlegend = FALSE)
}
# Simulation 1
set.seed(1)
traj1 <- simulate2(generate.input(1, 10))
# draw.simple(traj1)
# draw.speed(traj1)
# draw.3d(traj1)
# Simulation 2
set.seed(2)
traj2 <- simulate2(generate.input(1, 100))
# draw.simple(traj2)
# draw.speed(traj2)
# draw.3d(traj2)
# Simulation 3
set.seed(3)
traj3 <- simulate2(generate.input(2))
# draw.simple(traj3)
# draw.speed(traj3)
# draw.3d(traj3)