Implementation of an efficient algorithm for changepoint detection: ED-PELT
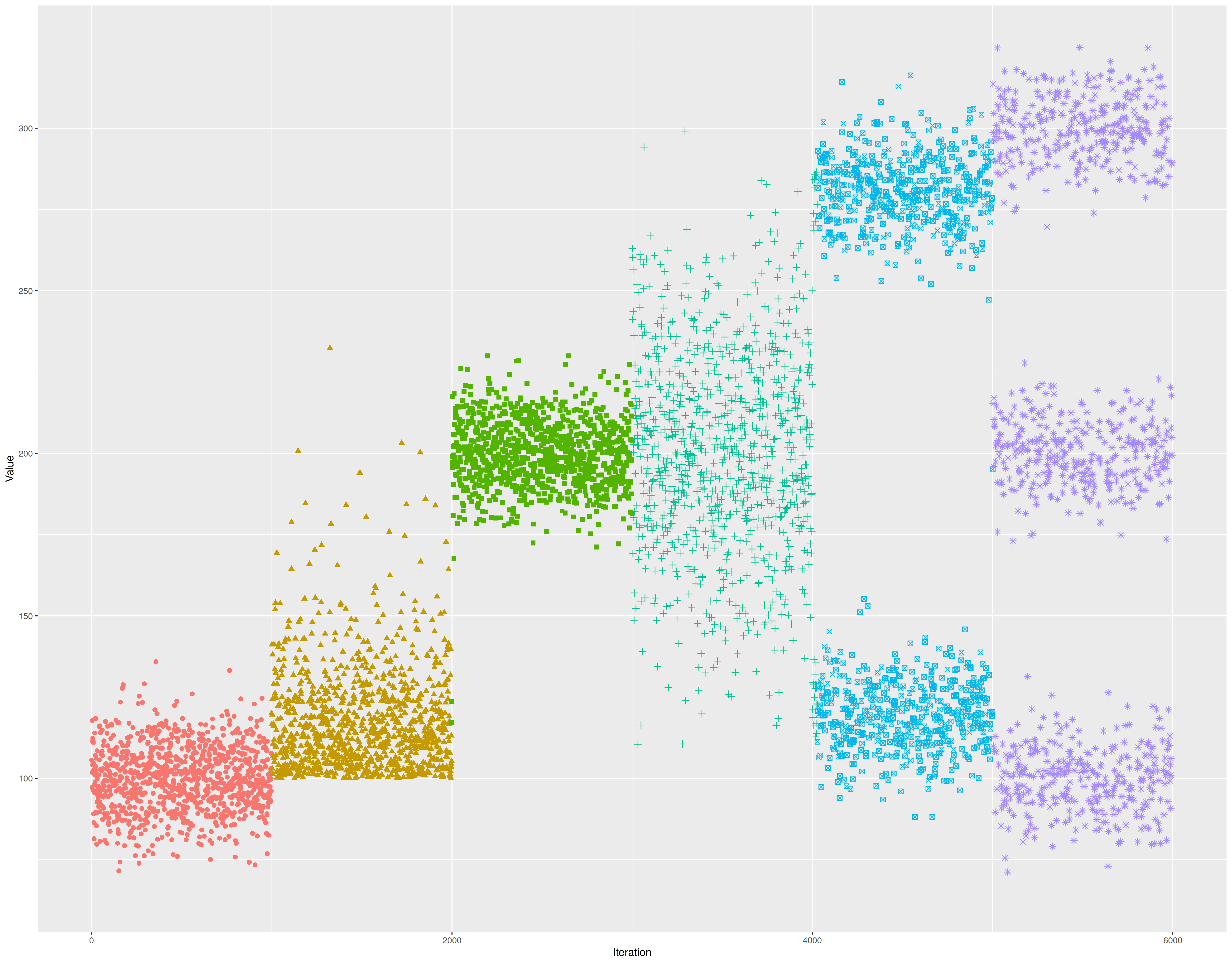
Changepoint detection is an important task that has a lot of applications. For example, I use it to detect changes in the Rider performance test suite. It’s very important to detect not only performance degradations, but any kinds of performance changes (e.g., the variance may increase, or an unimodal distribution may be split into several modes). You can see examples of such changes in the following picture (we change the color when a changepoint is detected):
Unfortunately, it’s pretty hard to write a reliable and fast algorithm for changepoint detection.
Recently, I found a cool paper A computationally efficient nonparametric approach for changepoint detection
By Kaylea Haynes, Paul Fearnhead, Idris A. Eckley
·
2016haynes2016 that describes the ED-PELT algorithm.
It has O(N*log(N)) complexity and pretty good detection accuracy.
The reference implementation can be used via the changepoint.np R package.
However, I can’t use R on our build server, so I decided to write my own C# implementation.
This implementation resolves the following problems:
- Portability
Below you can find a C# class that you can just copy-paste to your solution and play with it (you don’t have to install any NuGet packages and add other kinds of dependencies). If you are using another programming language, it should be pretty easy to port this code (let me know if you write another implementation, and I will add it to this blog post). I tried to comment on all the important steps, so you can understand what’s going on under the hood (it’s highly recommended to read the original paper first) and customize the algorithm for your own needs. - Performance
Performance is one of the most important features of this algorithm. I tried to make it as efficient as possible (keeping the code readable). With the help of some simple optimizations, I got a C# implementation that works much faster than the original R package (even though the ED-PELT core implementation in this package was written in C). - Better default parameters
The algorithm has a parameter callednquantiles. The paper recommends using4 * log(n)as the default value, but thechangepoint.npalways usenquantiles = 10. It leads to unreliable results for huge and small n values. Whenn < 10,changepoint.npworks incorrectly, a PR with a bug fix can be found here. Whenn >> 100,nquantiles = 10may be not enough to detect changes in multimodal distributions. All the examples in the official documentation override the default value with4 * log(n), but it’s not very convenient to do it each time.
The ED-PELT algorithm will be available out of the box in the next version of BenchmarkDotNet, but you can check it right now using the below implementation. I’m still not happy with the detection quality in some corner cases, so I’m going to improve it in the future. If you also have some problems with the presented implementation, let me know (my contacts can be found here).
ED-PELT implementation
The actual version of the algorithm is available in this gist.
// Copyright (c) 2019 Andrey Akinshin
// Licensed under The MIT License https://opensource.org/licenses/MIT
using System;
using System.Collections.Generic;
using System.Linq;
/// <summary>
/// The ED-PELT algorithm for changepoint detection.
///
/// <remarks>
/// The implementation is based on the following papers:
/// <list type="bullet">
/// <item>
/// <b>[Haynes2017]</b> Haynes, Kaylea, Paul Fearnhead, and Idris A. Eckley.
/// "A computationally efficient nonparametric approach for changepoint detection."
/// Statistics and Computing 27, no. 5 (2017): 1293-1305.
/// https://doi.org/10.1007/s11222-016-9687-5
/// </item>
/// <item>
/// <b>[Killick2012]</b> Killick, Rebecca, Paul Fearnhead, and Idris A. Eckley.
/// "Optimal detection of changepoints with a linear computational cost."
/// Journal of the American Statistical Association 107, no. 500 (2012): 1590-1598.
/// https://arxiv.org/pdf/1101.1438.pdf
/// </item>
/// </list>
/// </remarks>
/// </summary>
public class EdPeltChangePointDetector
{
public static readonly EdPeltChangePointDetector Instance = new EdPeltChangePointDetector();
/// <summary>
/// For given array of `double` values, detects locations of changepoints that
/// splits original series of values into "statistically homogeneous" segments.
/// Such points correspond to moments when statistical properties of the distribution are changing.
///
/// This method supports nonparametric distributions and has O(N*log(N)) algorithmic complexity.
/// </summary>
/// <param name="data">An array of double values</param>
/// <param name="minDistance">Minimum distance between changepoints</param>
/// <returns>
/// Returns an `int[]` array with 0-based indexes of changepoint.
/// Changepoints correspond to the end of the detected segments.
/// For example, changepoints for { 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2 } are { 5, 11 }.
/// </returns>
public int[] GetChangePointIndexes(double[] data, int minDistance = 1)
{
// We will use `n` as the number of elements in the `data` array
int n = data.Length;
// Checking corner cases
if (n <= 2)
return new int[0];
if (minDistance < 1 || minDistance > n)
throw new ArgumentOutOfRangeException(
nameof(minDistance),$"{minDistance} should be in range from 1 to data.Length");
// The penalty which we add to the final cost for each additional changepoint
// Here we use the Modified Bayesian Information Criterion
double penalty = 3 * Math.Log(n);
// `k` is the number of quantiles that we use to approximate an integral during the segment cost evaluation
// We use `k=Ceiling(4*log(n))` as suggested in the Section 4.3 "Choice of K in ED-PELT" in [Haynes2017]
// `k` can't be greater than `n`, so we should always use the `Min` function here (important for n <= 8)
int k = Math.Min(n, (int) Math.Ceiling(4 * Math.Log(n)));
// We should precalculate sums for empirical CDF, it will allow fast evaluating of the segment cost
var partialSums = GetPartialSums(data, k);
// Since we use the same values of `partialSums`, `k`, `n` all the time,
// we introduce a shortcut `Cost(tau1, tau2)` for segment cost evaluation.
// Hereinafter, we use `tau` to name variables that are changepoint candidates.
double Cost(int tau1, int tau2) => GetSegmentCost(partialSums, tau1, tau2, k, n);
// We will use dynamic programming to find the best solution; `bestCost` is the cost array.
// `bestCost[i]` is the cost for subarray `data[0..i-1]`.
// It's a 1-based array (`data[0]`..`data[n-1]` correspond to `bestCost[1]`..`bestCost[n]`)
var bestCost = new double[n + 1];
bestCost[0] = -penalty;
for (int currentTau = minDistance; currentTau < 2 * minDistance; currentTau++)
bestCost[currentTau] = Cost(0, currentTau);
// `previousChangePointIndex` is an array of references to previous changepoints. If the current segment ends at
// the position `i`, the previous segment ends at the position `previousChangePointIndex[i]`. It's a 1-based
// array (`data[0]`..`data[n-1]` correspond to the `previousChangePointIndex[1]`..`previousChangePointIndex[n]`)
var previousChangePointIndex = new int[n + 1];
// We use PELT (Pruned Exact Linear Time) approach which means that instead of enumerating all possible previous
// tau values, we use a whitelist of "good" tau values that can be used in the optimal solution. If we are 100%
// sure that some of the tau values will not help us to form the optimal solution, such values should be
// removed. See [Killick2012] for details.
var previousTaus = new List<int>(n + 1) { 0, minDistance };
var costForPreviousTau = new List<double>(n + 1);
// Following the dynamic programming approach, we enumerate all tau positions. For each `currentTau`, we pretend
// that it's the end of the last segment and trying to find the end of the previous segment.
for (int currentTau = 2 * minDistance; currentTau < n + 1; currentTau++)
{
// For each previous tau, we should calculate the cost of taking this tau as the end of the previous
// segment. This cost equals the cost for the `previousTau` plus cost of the new segment (from `previousTau`
// to `currentTau`) plus penalty for the new changepoint.
costForPreviousTau.Clear();
foreach (int previousTau in previousTaus)
costForPreviousTau.Add(bestCost[previousTau] + Cost(previousTau, currentTau) + penalty);
// Now we should choose the tau that provides the minimum possible cost.
int bestPreviousTauIndex = WhichMin(costForPreviousTau);
bestCost[currentTau] = costForPreviousTau[bestPreviousTauIndex];
previousChangePointIndex[currentTau] = previousTaus[bestPreviousTauIndex];
// Prune phase: we remove "useless" tau values that will not help to achieve minimum cost in the future
double currentBestCost = bestCost[currentTau];
int newPreviousTausSize = 0;
for (int i = 0; i < previousTaus.Count; i++)
if (costForPreviousTau[i] < currentBestCost + penalty)
previousTaus[newPreviousTausSize++] = previousTaus[i];
previousTaus.RemoveRange(newPreviousTausSize, previousTaus.Count - newPreviousTausSize);
// We add a new tau value that is located on the `minDistance` distance from the next `currentTau` value
previousTaus.Add(currentTau - (minDistance - 1));
}
// Here we collect the result list of changepoint indexes `changePointIndexes` using `previousChangePointIndex`
var changePointIndexes = new List<int>();
int currentIndex = previousChangePointIndex[n]; // The index of the end of the last segment is `n`
while (currentIndex != 0)
{
changePointIndexes.Add(currentIndex - 1); // 1-based indexes should be be transformed to 0-based indexes
currentIndex = previousChangePointIndex[currentIndex];
}
changePointIndexes.Reverse(); // The result changepoints should be sorted in ascending order.
return changePointIndexes.ToArray();
}
/// <summary>
/// Partial sums for empirical CDF (formula (2.1) from Section 2.1 "Model" in [Haynes2017])
/// <code>
/// partialSums[i, tau] = (count(data[j] < t) * 2 + count(data[j] == t) * 1) for j=0..tau-1
/// where t is the i-th quantile value (see Section 3.1 "Discrete approximation" in [Haynes2017] for details)
/// </code>
/// <remarks>
/// <list type="bullet">
/// <item>
/// We use doubled sum values in order to use <c>int[,]</c> instead of <c>double[,]</c> (it provides noticeable
/// performance boost). Thus, multipliers for <c>count(data[j] < t)</c> and <c>count(data[j] == t)</c> are
/// 2 and 1 instead of 1 and 0.5 from the [Haynes2017].
/// </item>
/// <item>
/// Note that these quantiles are not uniformly distributed: tails of the <c>data</c> distribution contain more
/// quantile values than the center of the distribution
/// </item>
/// </list>
/// </remarks>
/// </summary>
private static int[,] GetPartialSums(double[] data, int k)
{
int n = data.Length;
var partialSums = new int[k, n + 1];
var sortedData = data.OrderBy(it => it).ToArray();
for (int i = 0; i < k; i++)
{
double z = -1 + (2 * i + 1.0) / k; // Values from (-1+1/k) to (1-1/k) with step = 2/k
double p = 1.0 / (1 + Math.Pow(2 * n - 1, -z)); // Values from 0.0 to 1.0
double t = sortedData[(int) Math.Truncate((n - 1) * p)]; // Quantile value, formula (2.1) in [Haynes2017]
for (int tau = 1; tau <= n; tau++)
{
partialSums[i, tau] = partialSums[i, tau - 1];
if (data[tau - 1] < t)
partialSums[i, tau] += 2; // We use doubled value (2) instead of original 1.0
if (data[tau - 1] == t)
partialSums[i, tau] += 1; // We use doubled value (1) instead of original 0.5
}
}
return partialSums;
}
/// <summary>
/// Calculates the cost of the (tau1; tau2] segment.
/// </summary>
private static double GetSegmentCost(int[,] partialSums, int tau1, int tau2, int k, int n)
{
double sum = 0;
for (int i = 0; i < k; i++)
{
// actualSum is (count(data[j] < t) * 2 + count(data[j] == t) * 1) for j=tau1..tau2-1
int actualSum = partialSums[i, tau2] - partialSums[i, tau1];
// We skip these two cases (correspond to fit = 0 or fit = 1) because of invalid Math.Log values
if (actualSum != 0 && actualSum != (tau2 - tau1) * 2)
{
// Empirical CDF $\hat{F}_i(t)$ (Section 2.1 "Model" in [Haynes2017])
double fit = actualSum * 0.5 / (tau2 - tau1);
// Segment cost $\mathcal{L}_{np}$ (Section 2.2 "Nonparametric maximum likelihood" in [Haynes2017])
double lnp = (tau2 - tau1) * (fit * Math.Log(fit) + (1 - fit) * Math.Log(1 - fit));
sum += lnp;
}
}
double c = -Math.Log(2 * n - 1); // Constant from Lemma 3.1 in [Haynes2017]
return 2.0 * c / k * sum; // See Section 3.1 "Discrete approximation" in [Haynes2017]
}
/// <summary>
/// Returns the index of the minimum element.
/// In case if there are several minimum elements in the given list, the index of the first one will be returned.
/// </summary>
private static int WhichMin(IList<double> values)
{
if (values.Count == 0)
throw new InvalidOperationException("Array should contain elements");
double minValue = values[0];
int minIndex = 0;
for (int i = 1; i < values.Count; i++)
if (values[i] < minValue)
{
minValue = values[i];
minIndex = i;
}
return minIndex;
}
}