Sensitivity curve of the Harrell-Davis quantile estimator, Part 2

Andrey Akinshin · 2022-10-04

In the previous post, I have explored the sensitivity curves of the Harrell-Davis quantile estimator on the normal distribution. In this post, I continue the same investigation on the exponential and Cauchy distributions.

The classic Harrell-Davis quantile estimator (see A new distribution-free quantile estimator
By Frank E Harrell, C E Davis · 1982harrell1982) is defined as follows:

$$ Q_{\operatorname{HD}}(p) = \sum_{i=1}^{n} W_{\operatorname{HD},i} \cdot x_{(i)},\quad W_{\operatorname{HD},i} = I_{i/n}(\alpha, \beta) - I_{(i-1)/n}(\alpha, \beta), $$

where $I_t(\alpha, \beta)$ is the regularized incomplete beta function, $\alpha = (n+1)p$, $\;\beta = (n+1)(1-p)$. In this post we consider the Harrell-Davis median estimator $Q_{\operatorname{HD}}(0.5)$.

The standardized sensitivity curve (SC) of an estimator $\hat{\theta}$ is given by

$$ \operatorname{SC}_n(x_0) = \frac{ \hat{\theta}_{n+1}(x_1, x_2, \ldots, x_n, x_0) - \hat{\theta}_n(x_1, x_2, \ldots, x_n) }{1 / (n + 1)} $$

Thus, the SC shows the standardized change of the estimator value for situation, when we add a new element $x_0$ to an existing sample $\mathbf{x} = \{ x_1, x_2, \ldots, x_n \}$. In the context of this post, we perform simulations using the exponential and Cauchy distributions given by their quantile functions that we denote as $F^{-1}$. Following the approach from [Maronna2019, Section 3.1], we define the sample $\mathbf{x}$ as

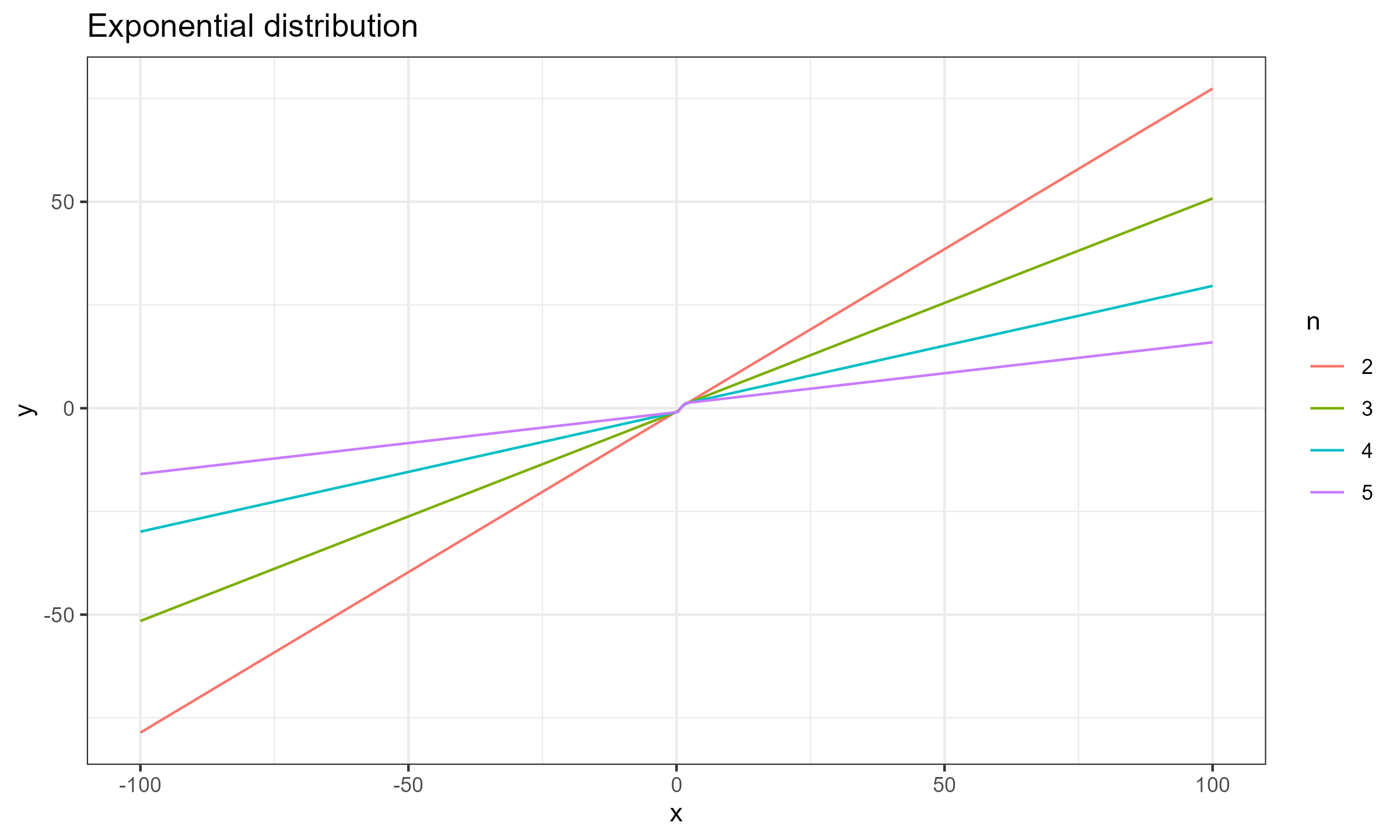
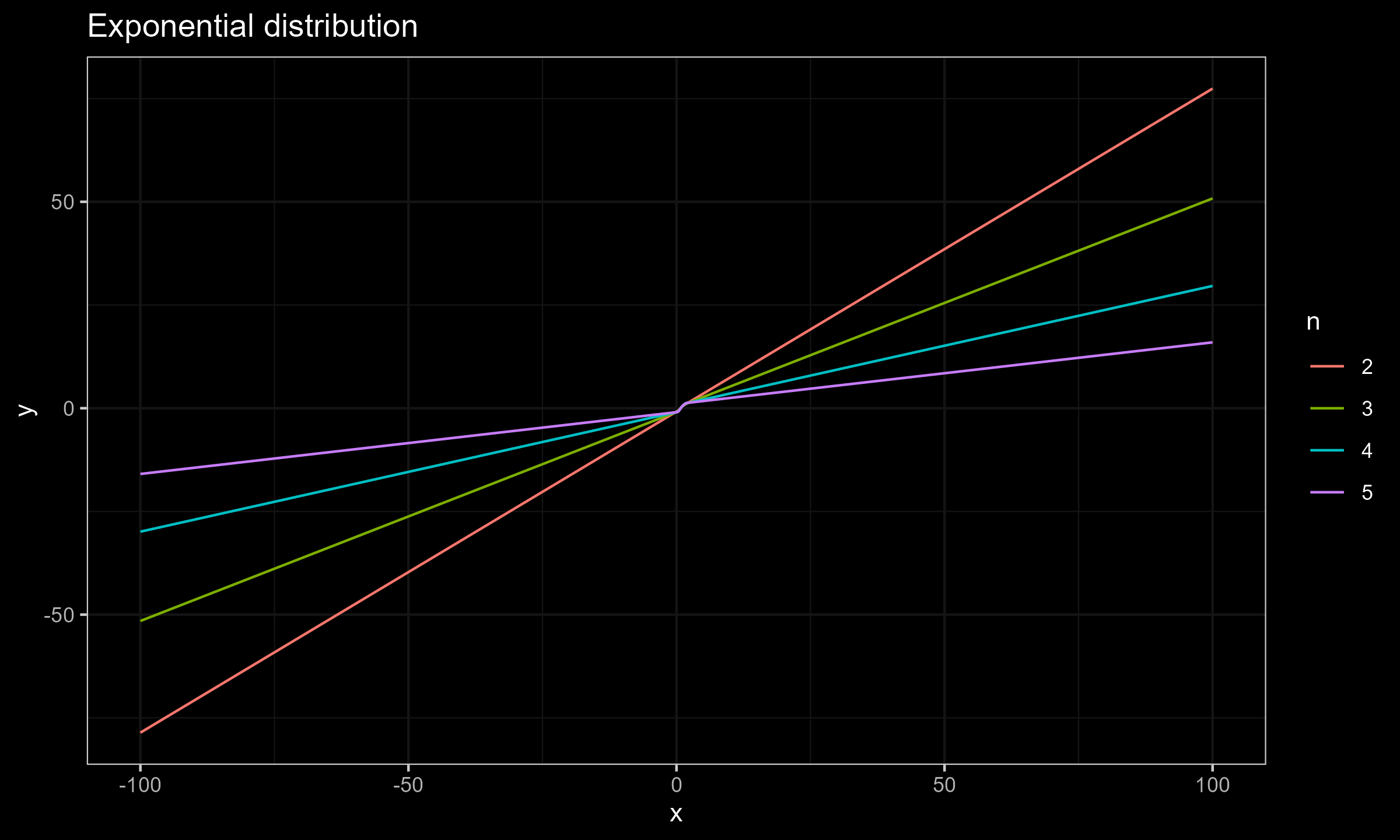
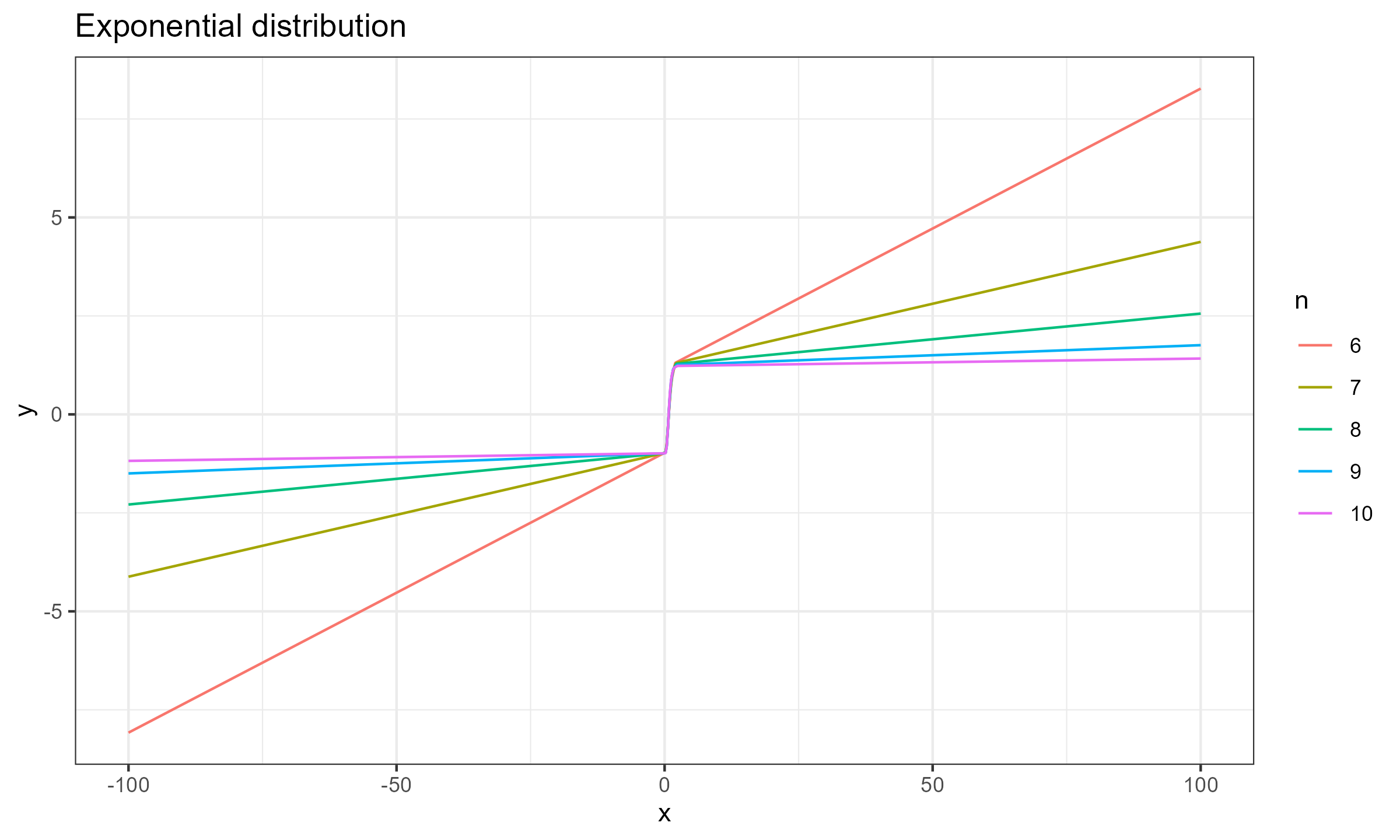
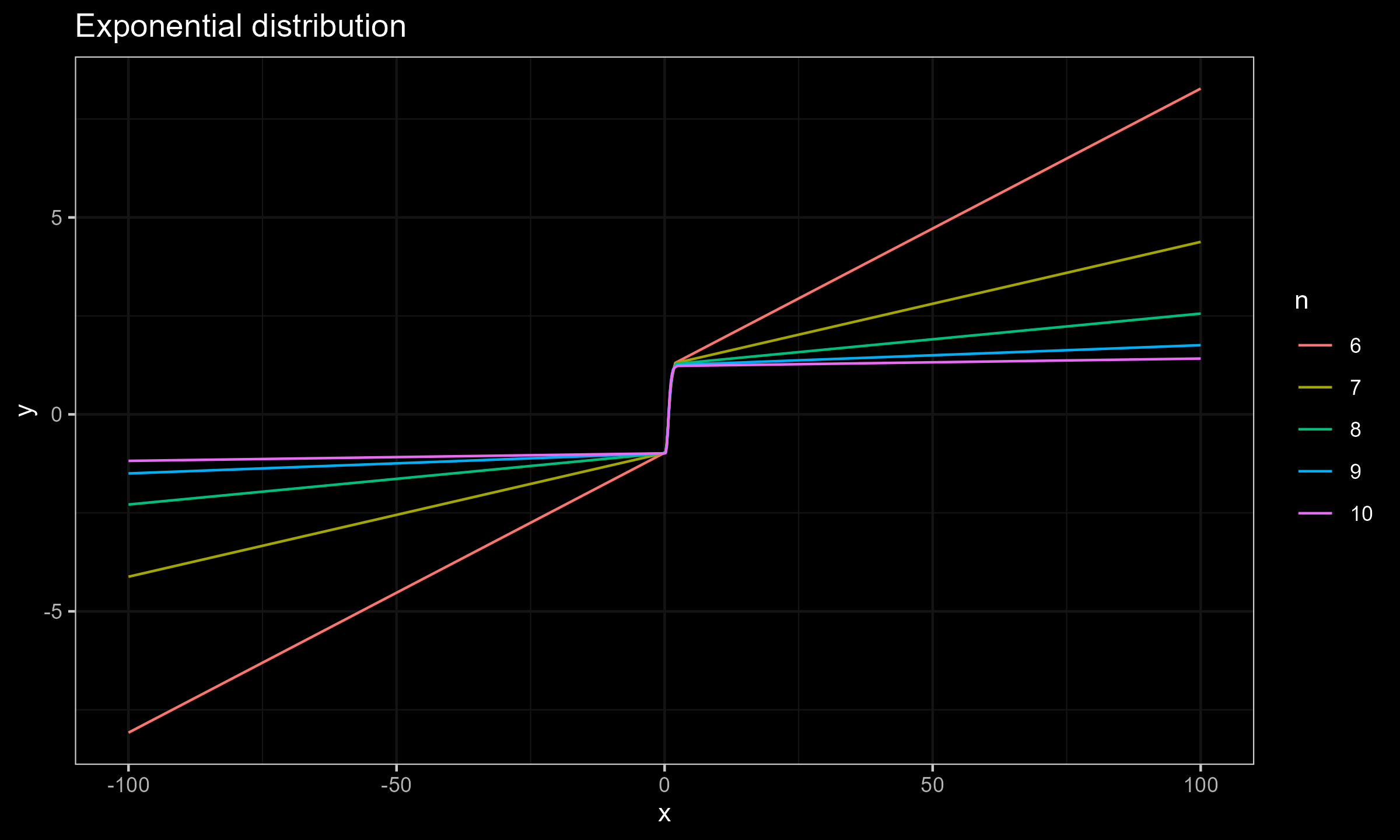
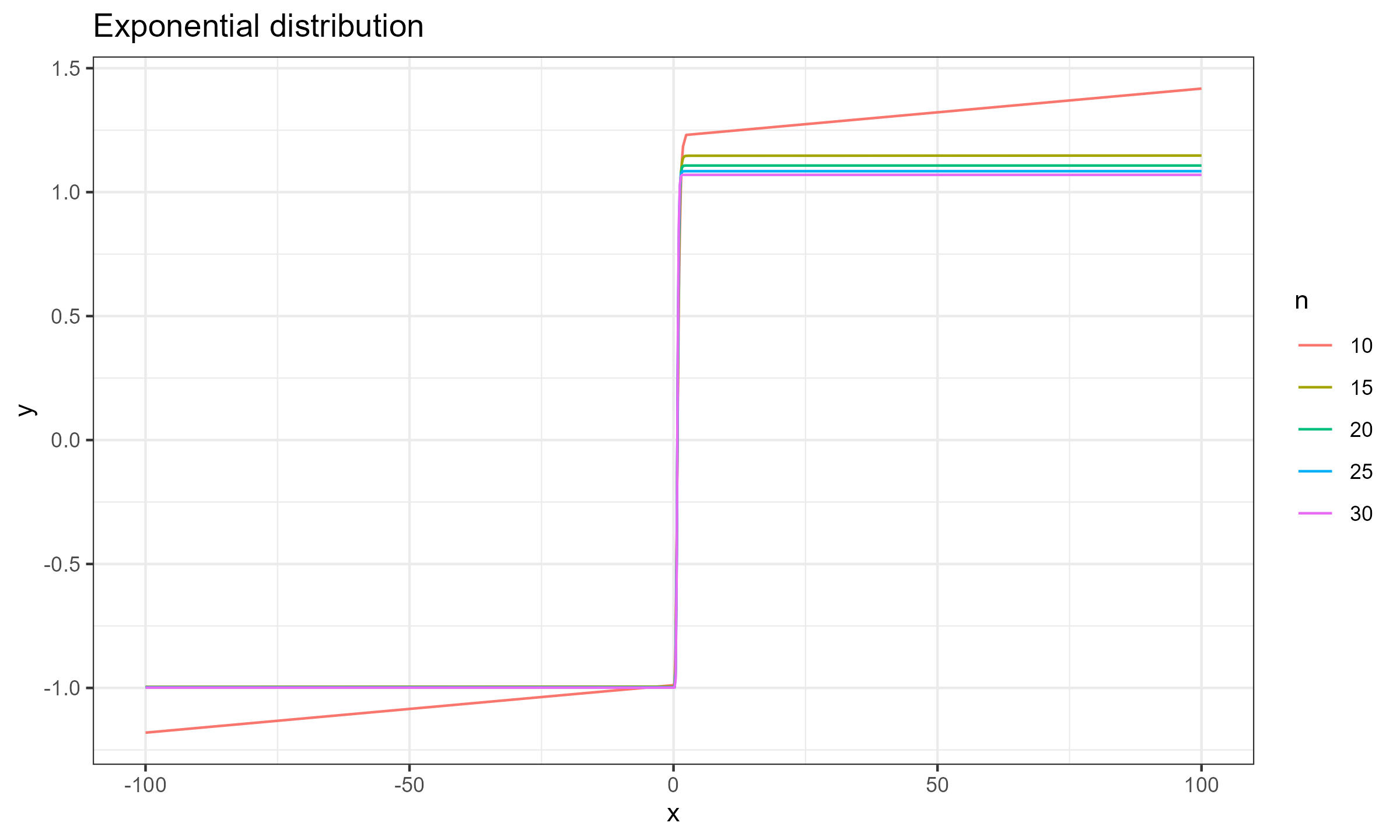
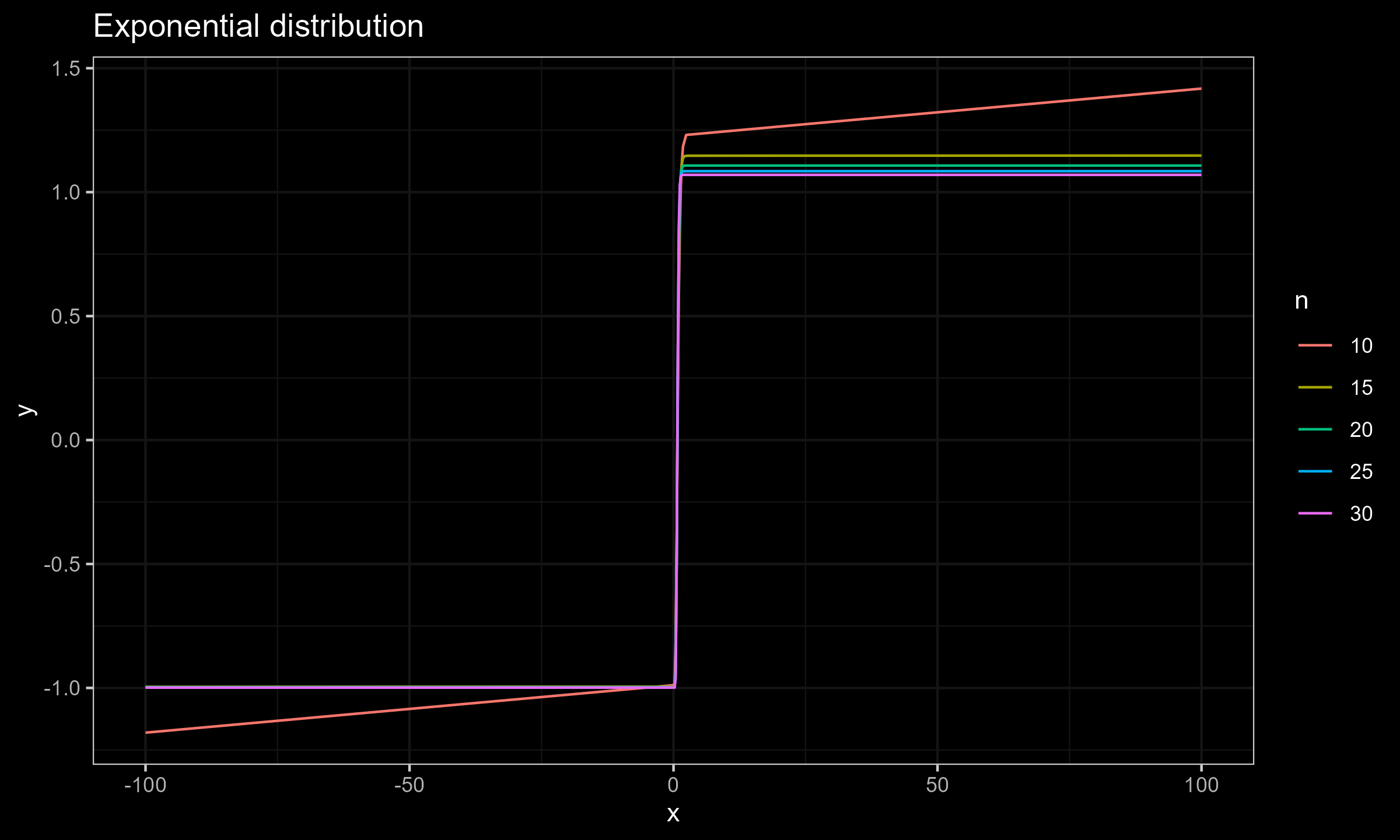
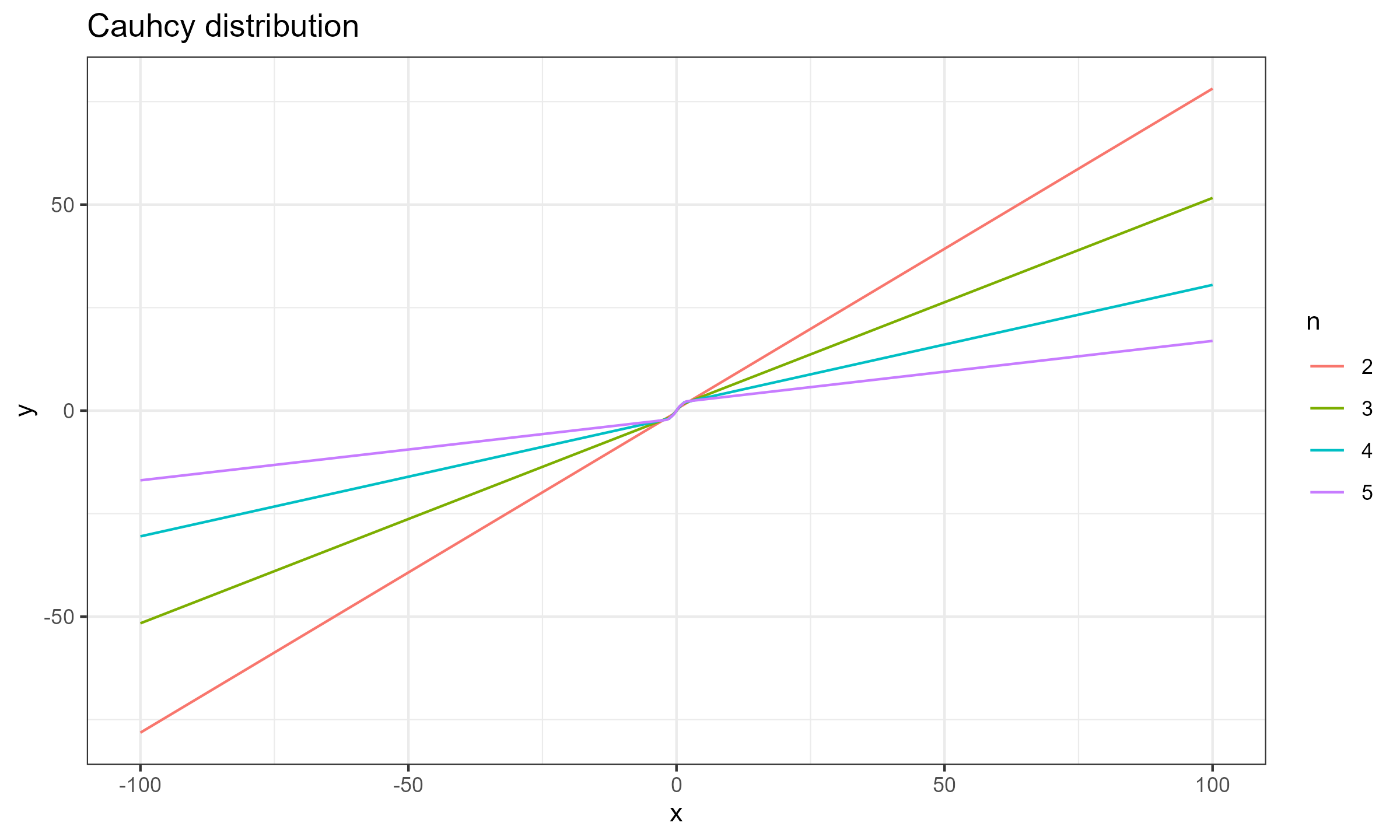
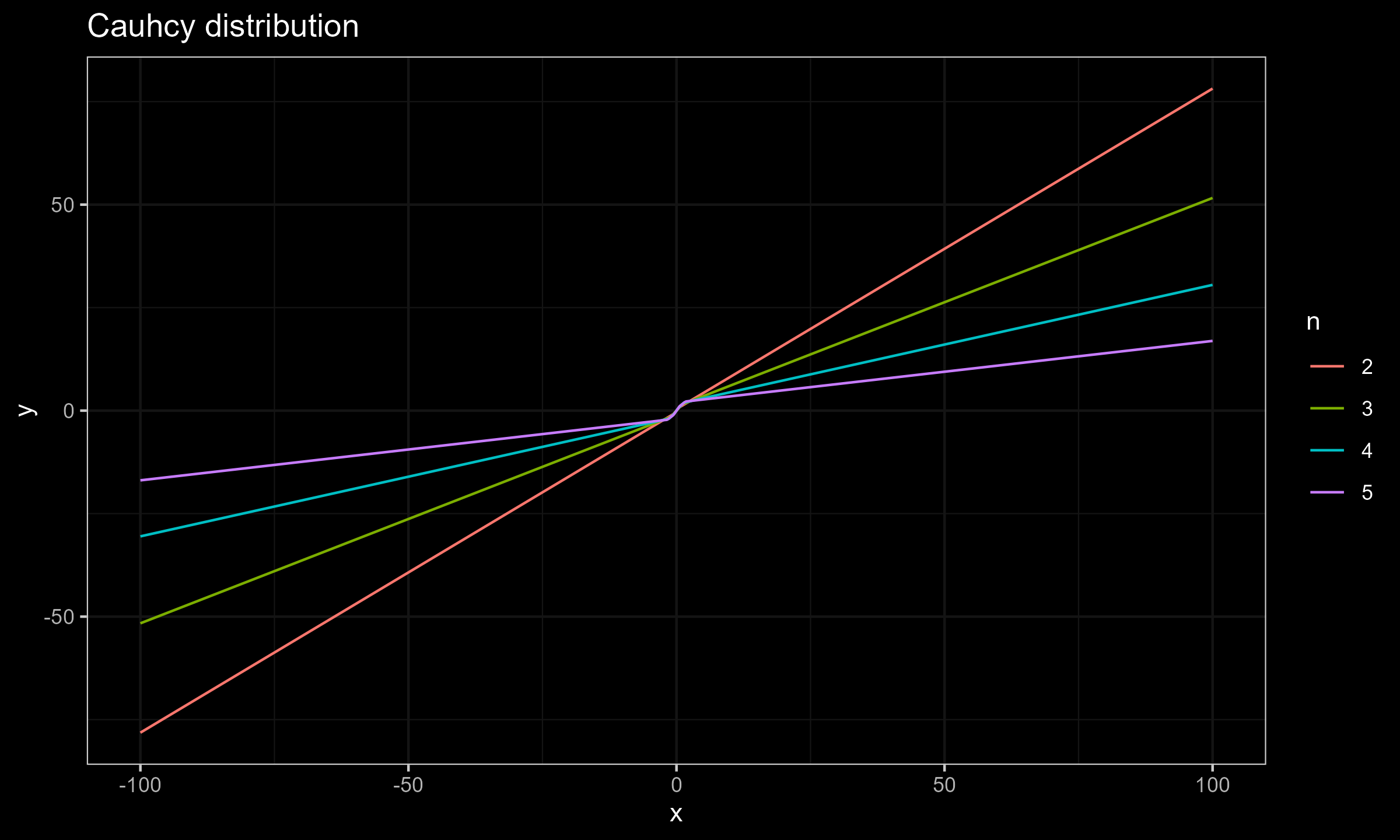
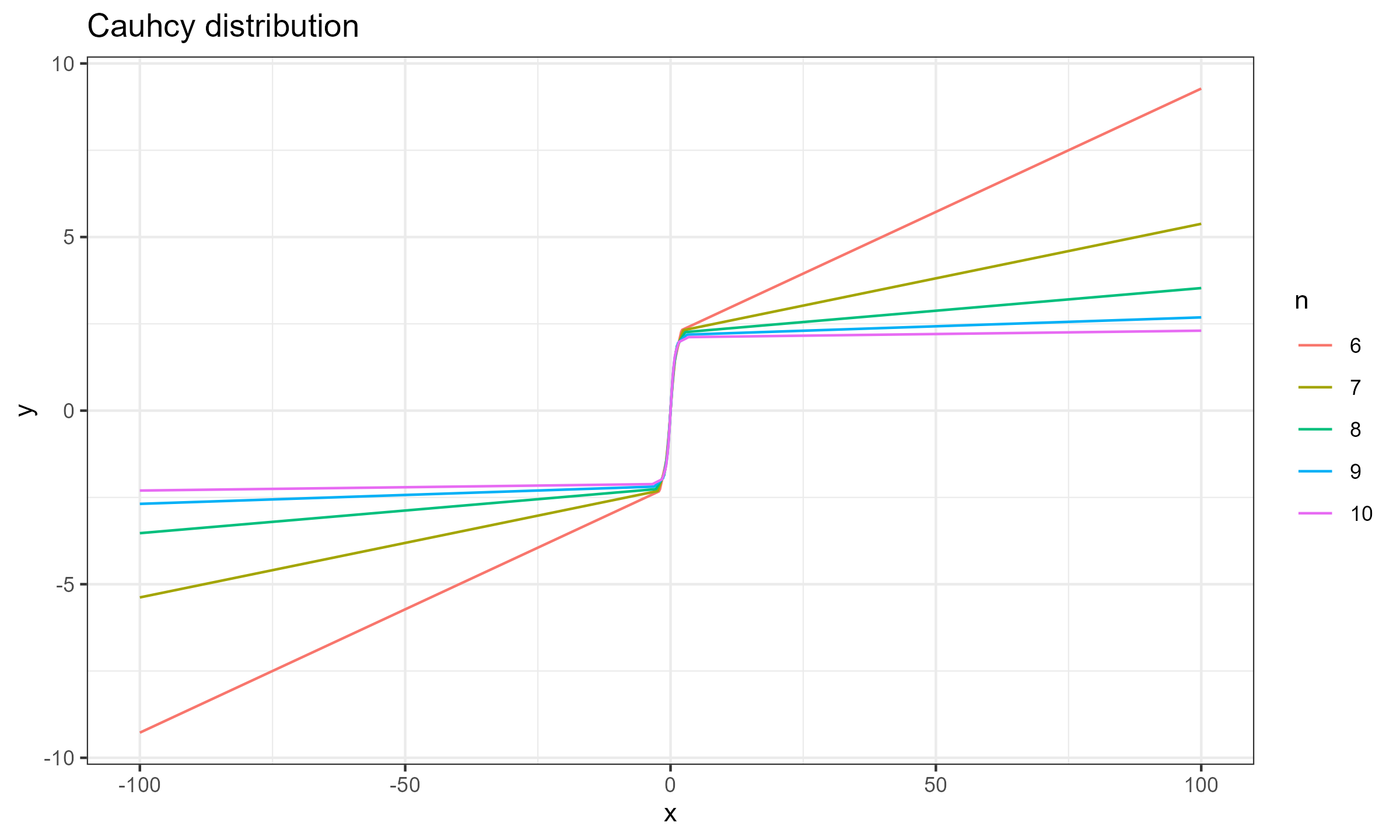
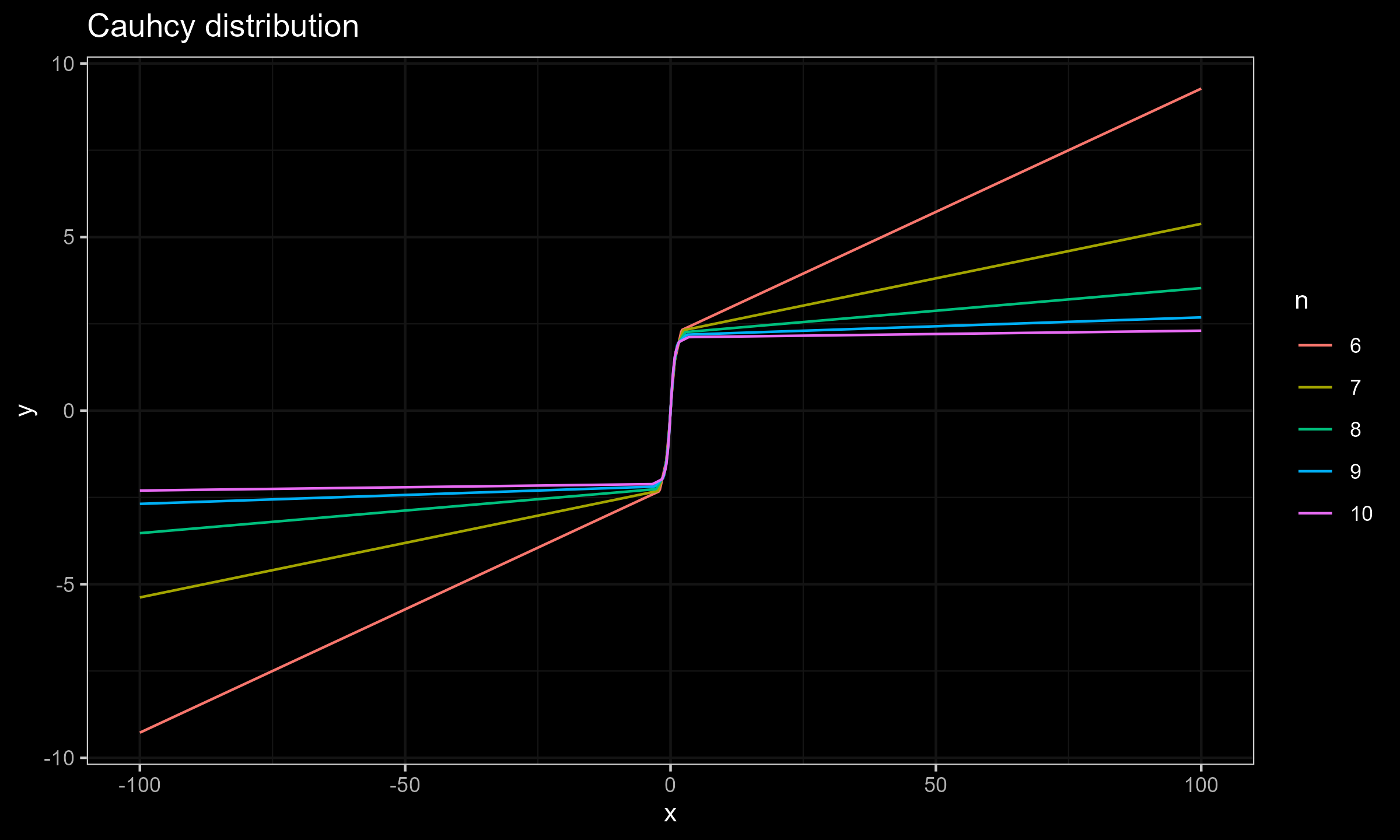
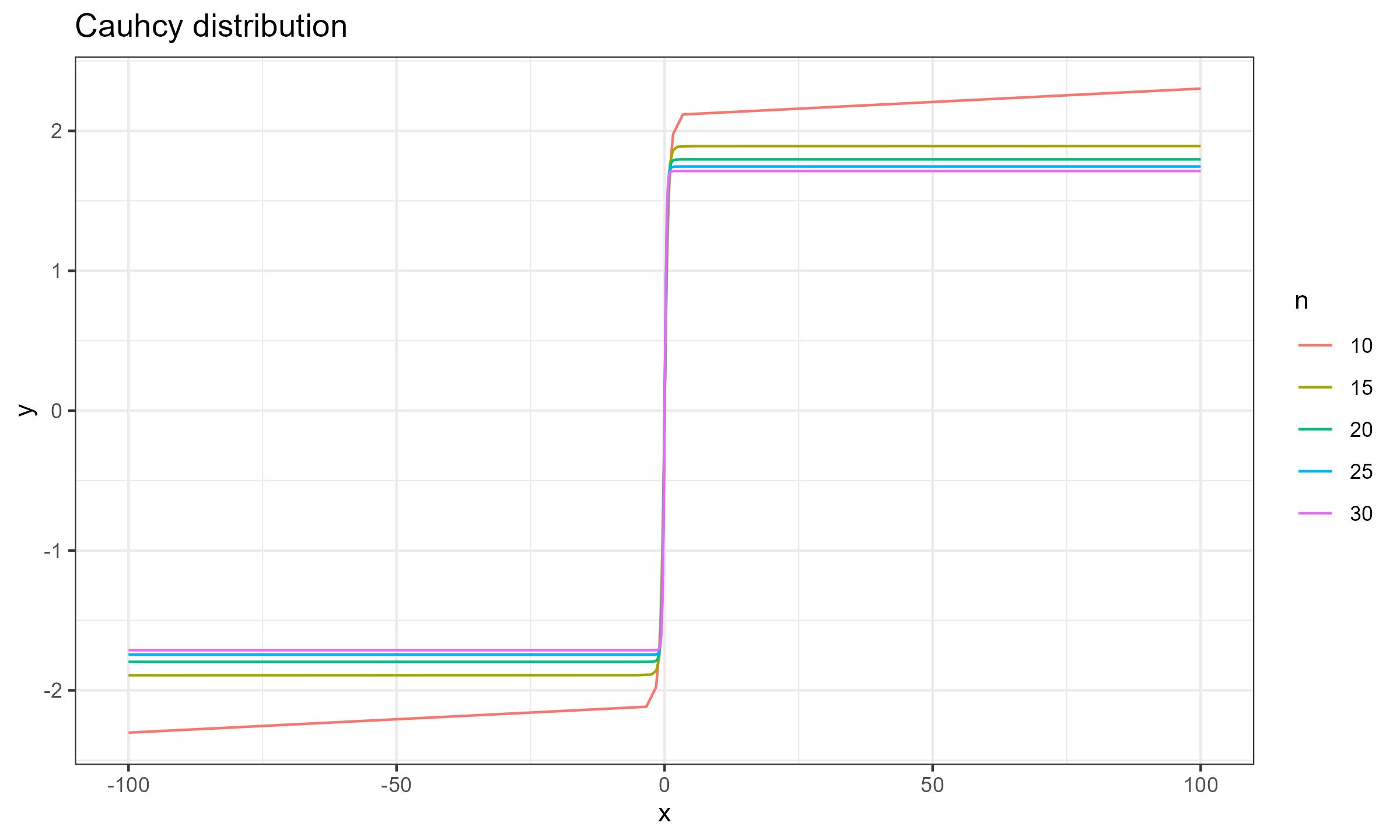
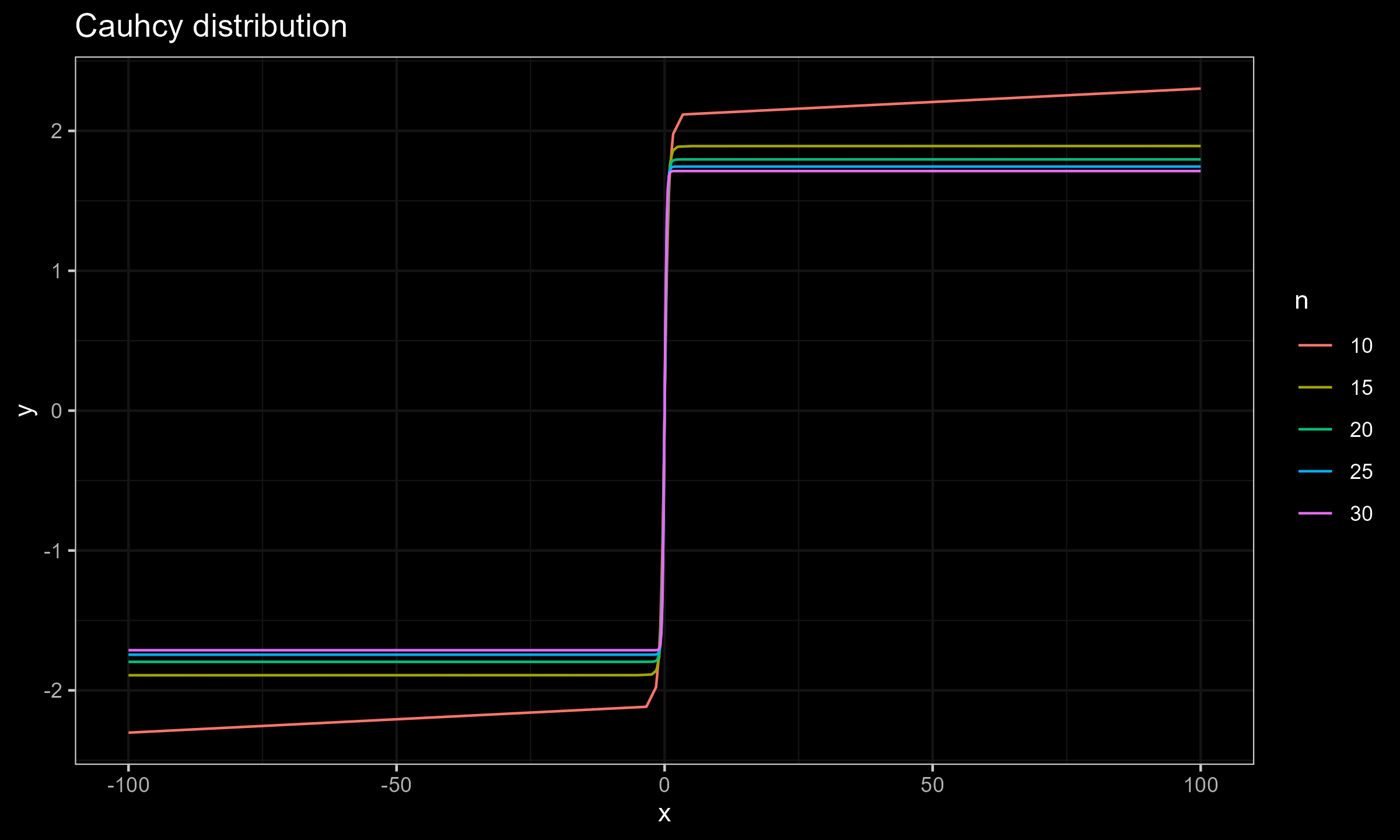
$$ \mathbf{x} = \Bigg\{ F^{-1}\Big(\frac{1}{n+1}\Big), F^{-1}\Big(\frac{2}{n+1}\Big), \ldots, F^{-1}\Big(\frac{n}{n+1}\Big) \Bigg\} $$

Now let’s explore the SC values for different sample sizes for $x_0 \in [-100; 100]$.

Exponential distribution

Cauchy distribution

Conclusion

As we can see, for $n \geq 15$ the actual impact of $x_0$ is negligible, which makes the Harrell-Davis median estimator a practically reasonable choice. This conclusion is relevant not only for the normal distribution (as shown in the previous post), but also for the exponential distribution and the Cauchy distribution.

References

  • [Harrell1982]
    Harrell, F.E. and Davis, C.E., 1982. A new distribution-free quantile estimator. Biometrika, 69(3), pp.635-640.
    https://doi.org/10.2307/2335999
  • [Maronna2019]
    Maronna, Ricardo A., R. Douglas Martin, Victor J. Yohai, and Matías Salibián-Barrera. Robust statistics: theory and methods (with R). John Wiley & Sons, 2019.