Ratio estimator based on the Hodges-Lehmann approach

This post introduces a ratio estimator for multiplicative differences between two samples, built on the Hodges–Lehmann framework via a log-exp transform. In Pragmastat, this is Ratio — the recommended robust multiplicative difference estimator. Confidence intervals are available via RatioBounds.

pragmastat.dev github.com/AndreyAkinshin/pragmastat

For two samples $\mathbf{x} = ( x_1, x_2, \ldots, x_n )$ and $\mathbf{y} = ( y_1, y_2, \ldots, y_m )$, the Hodges-Lehmann EstimatorHodges-Lehmann location shift estimator is defined as follows:

$$ \operatorname{HL}(\mathbf{x}, \mathbf{y}) = \underset{1 \leq i \leq n,\,\, 1 \leq j \leq m}{\operatorname{median}} \left(x_i - y_j \right). $$

Now, let us consider the problem of estimating the ratio of the location measures instead of the shift between them. While there are multiple approaches to providing such an estimation, one of the options that can be considered is based on the Hodges-Lehmann ideas.

More specifically, we can introduce the following ratio estimator:

$$ \operatorname{HLR}(\mathbf{x}, \mathbf{y}) = \underset{1 \leq i \leq n,\,\, 1 \leq j \leq m}{\operatorname{median}} \left(x_i / y_j \right). $$

Of course, ratio estimation is applicable only when the random variables are positive and therefore $x_i, y_j > 0$.

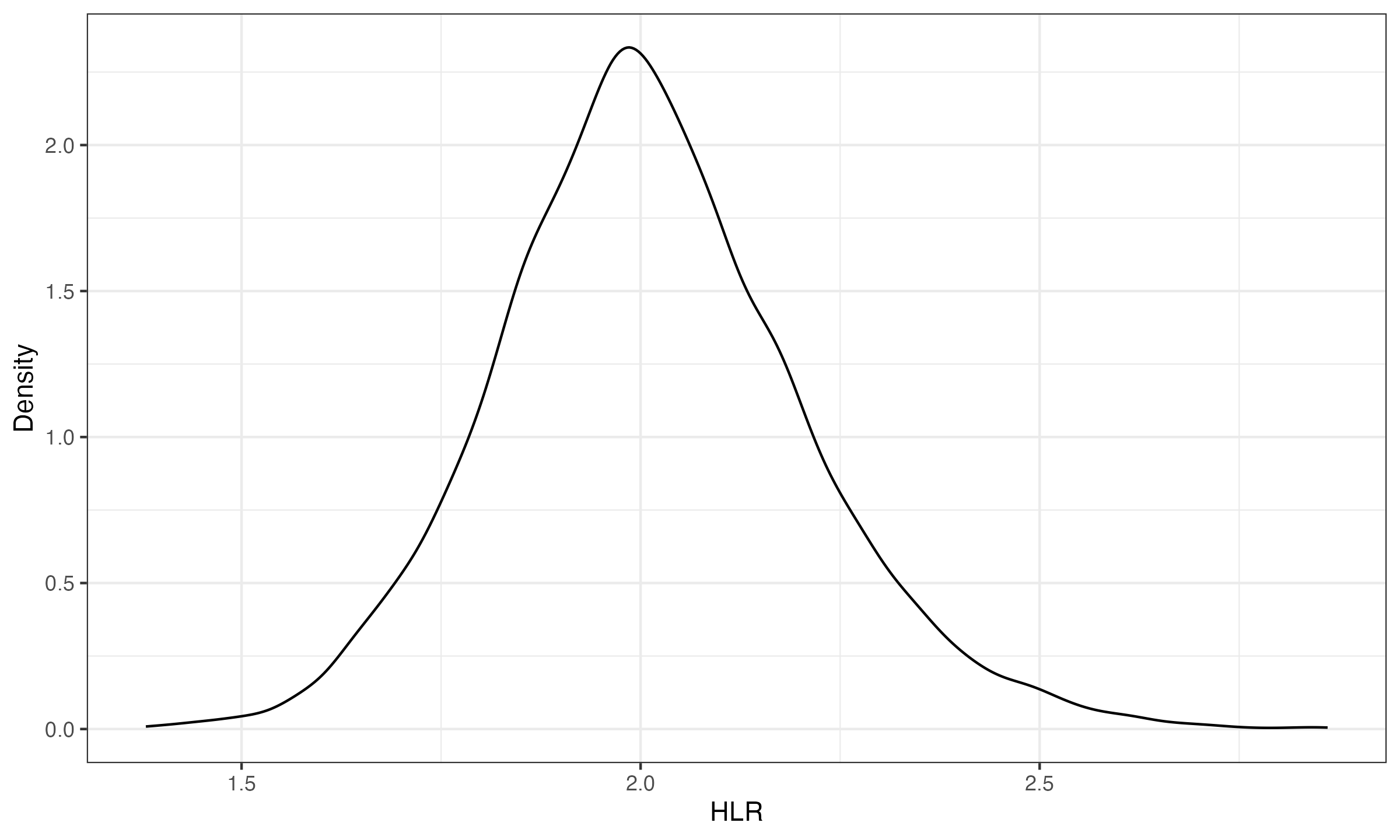
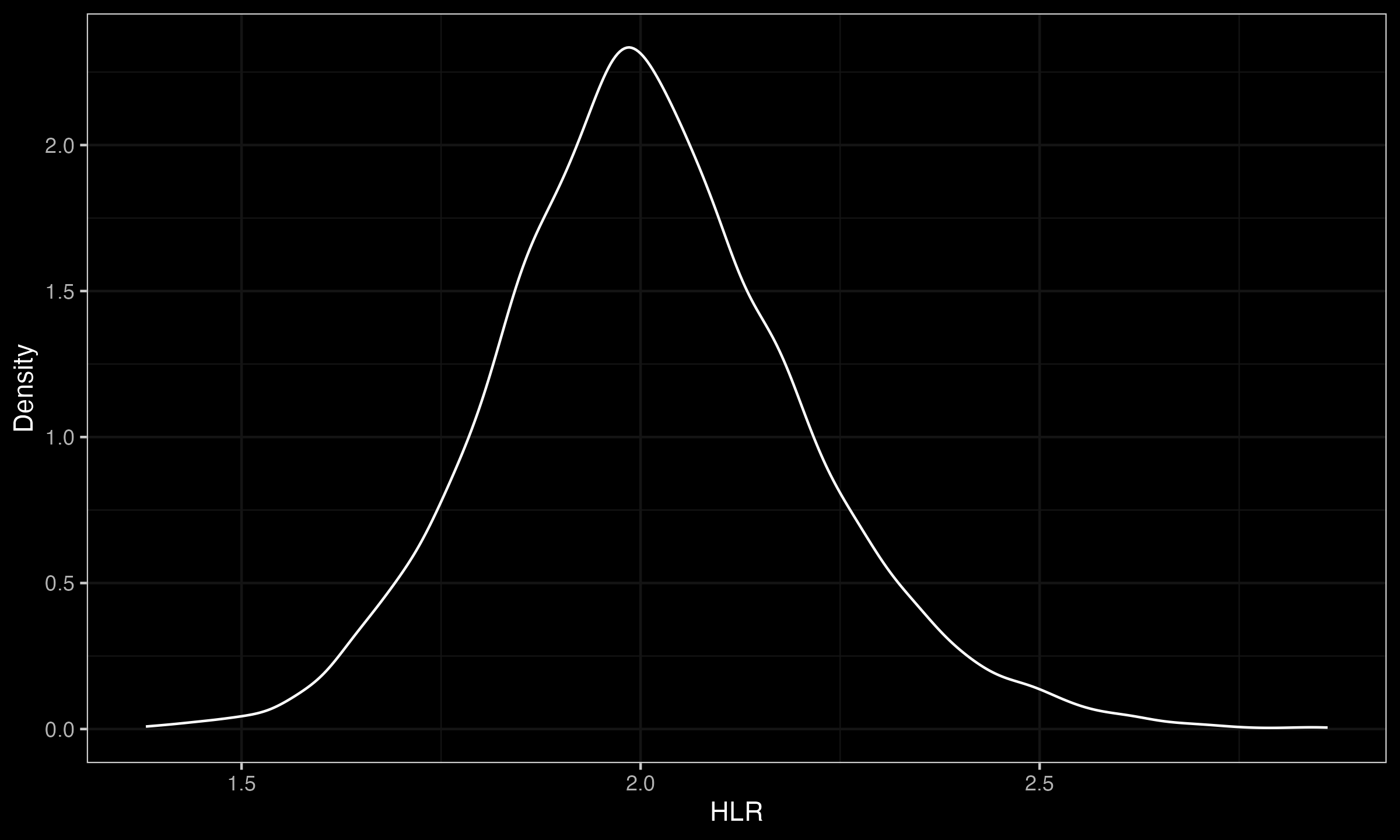
To illustrate $\operatorname{HLR}$, we compare the its sampling distribution for $x_i \sim \mathcal{U}(20, 40)$, $y_j \sim \mathcal{U}(10, 20)$ for $n=m=10$:

As we can see, the sampling distribution mode is about $2$, which matches our expectations. In the further posts, we will compare this approach to other existing ration estimator and perform a comparison of their biases and statistical efficiency.