Statistical efficiency of the Hodges-Lehmann median estimator, Part 1

Andrey Akinshin · 2022-05-17

In this post, we evaluate the relative statistical efficiency of the Hodges-Lehmann EstimatorHodges-Lehmann Estimator against the sample median under the normal distribution. We also compare it with the efficiency of the Harrell-Davis quantile estimator.

Introduction

The Hodges-Lehmann median estimator is defined as the sample median of all pair-wise averages of the given sample. However, there are various ways to define an explicit formula. Following an approach from Investigation of finite-sample properties of robust location and scale estimators
By Chanseok Park, Haewon Kim, Min Wang · 2020park2020, we consider three options:

$$ \operatorname{HL}_1 = \underset{i < j}{\operatorname{median}}\Big(\frac{x_i + x_j}{2}\Big),\quad \operatorname{HL}_2 = \underset{i \leq j}{\operatorname{median}}\Big(\frac{x_i + x_j}{2}\Big),\quad \operatorname{HL}_3 = \underset{\forall i, j}{\operatorname{median}}\Big(\frac{x_i + x_j}{2}\Big). $$

We also consider the classic Harrell-Davis quantile estimator which can also be used to estimate the median:

$$ Q_\textrm{HD}(p) = \sum_{i=1}^{n} W_{i} \cdot x_{(i)}, \quad W_{i} = I_{i/n}(a, b) - I_{(i-1)/n}(a, b), \quad a = p(n+1),\; b = (1-p)(n+1) $$

where $I_t(a, b)$ denotes the regularized incomplete beta function, $x_{(i)}$ is the $i^\textrm{th}$ order statistics.

Simulation study

In order to evaluate the relative statistical efficiency of the listed median estimators against the sample median, we use the following scheme:

  • Enumerate different sample size values $n$ from $3$ to $30$.
  • For each sample size, we generate $10\,000$ samples from the normal distribution.
  • For each sample, we estimate the median using the sample median, the Harrell-Davis quantile estimator, and three versions of the Hodges-Lehmann median estimator.
  • Since all considered estimators are unbiased under the normal distribution, the relative statistical efficiency is just a ratio between the variance of the sample median and the variance of the target median estimator.

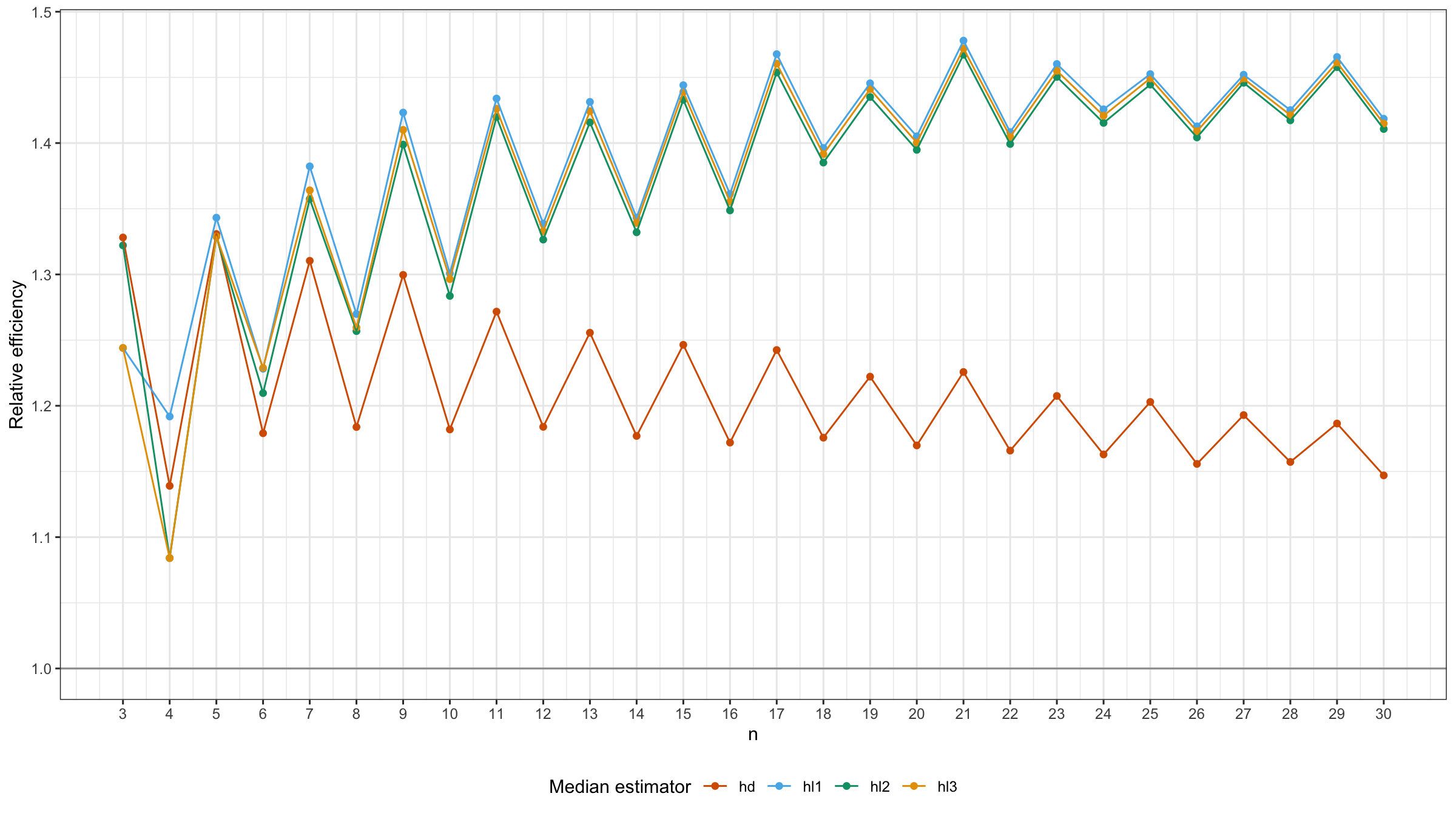
The results of the performed simulation study are shown in the following figure:

As we can see, for $n\geq 6$, all three versions of the Hodges-Lehmann median estimator outperform the Harrell-Davis quantile estimator in terms of relative statistical efficiency under the normal distribution.

In the next post, we perform more simulations study to get a better understanding of the properties of the Hodges-Lehmann median estimator.