Quantile estimators based on k order statistics, Part 6: Continuous trimmed Harrell-Davis quantile estimator

In my previous post, I tried the idea of using the trimmed modification of the Harrell-Davis quantile estimator based on the highest density interval of the given width. The width was defined so that it covers exactly k order statistics (the width equals $(k-1)/n$). I was pretty satisfied with the result and decided to continue evolving this approach. While “k order statistics” is a good mental model that described the trimmed interval, it doesn’t actually require an integer k. In fact, we can use any real number as the trimming percentage.

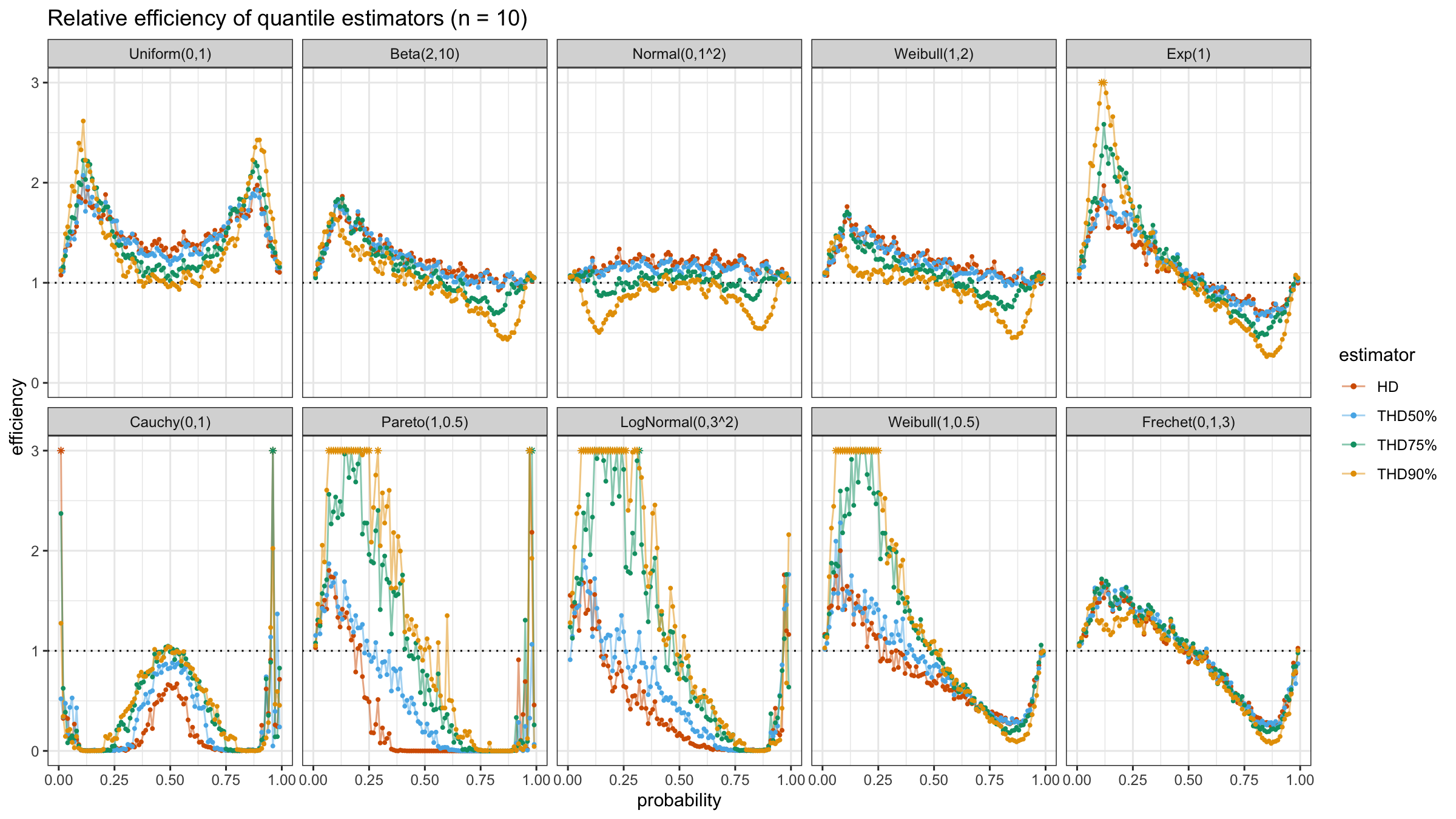
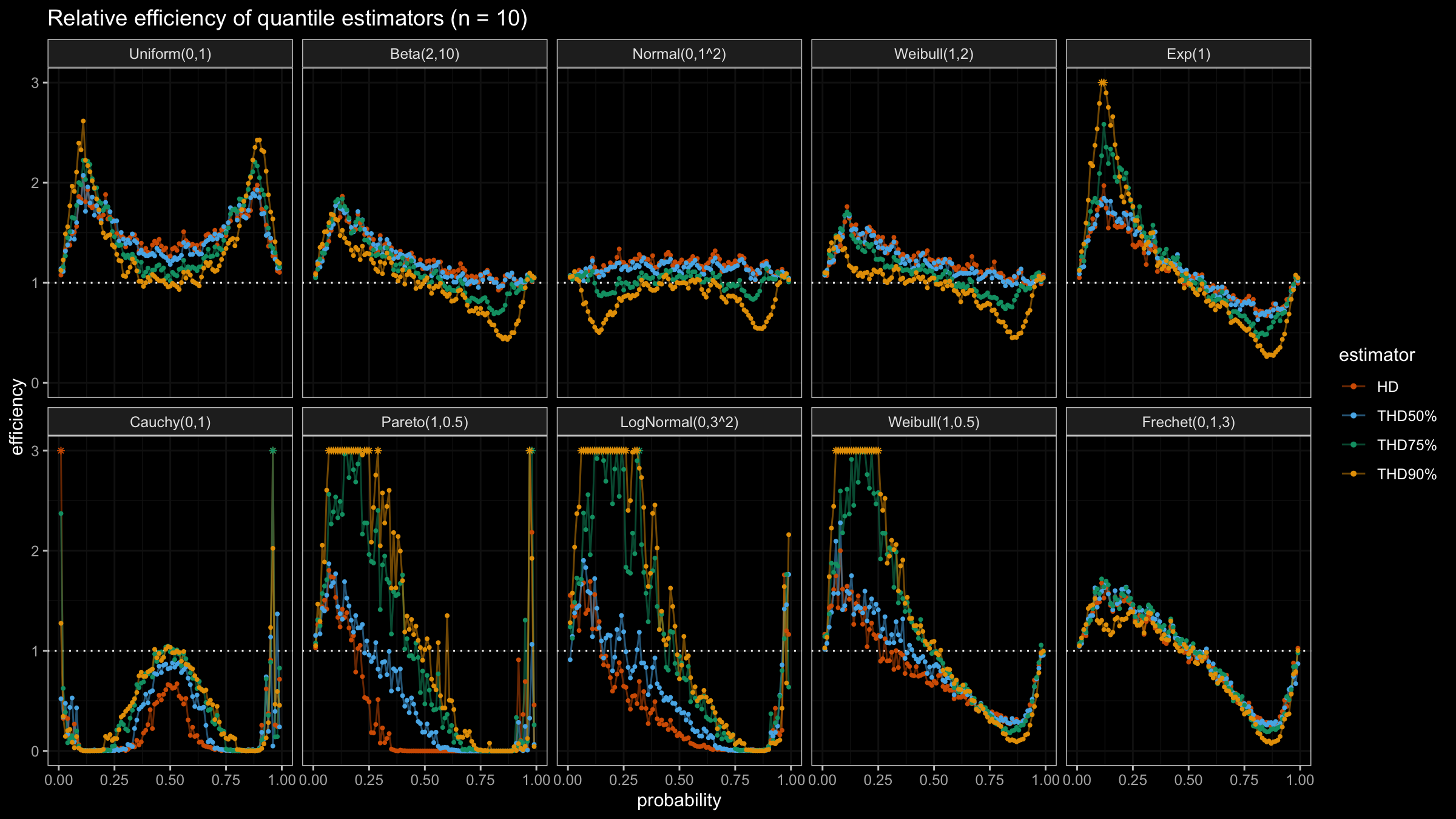
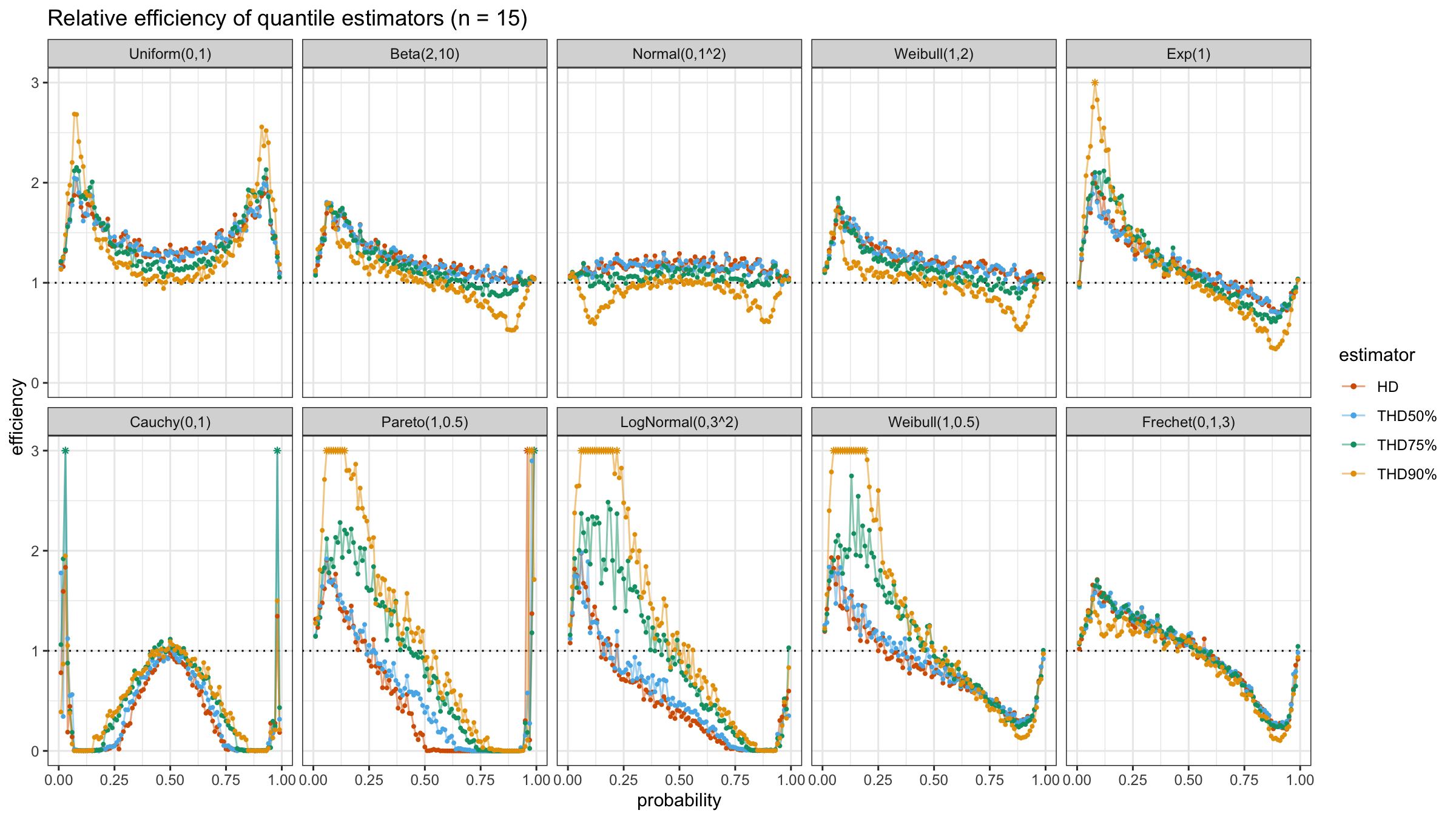
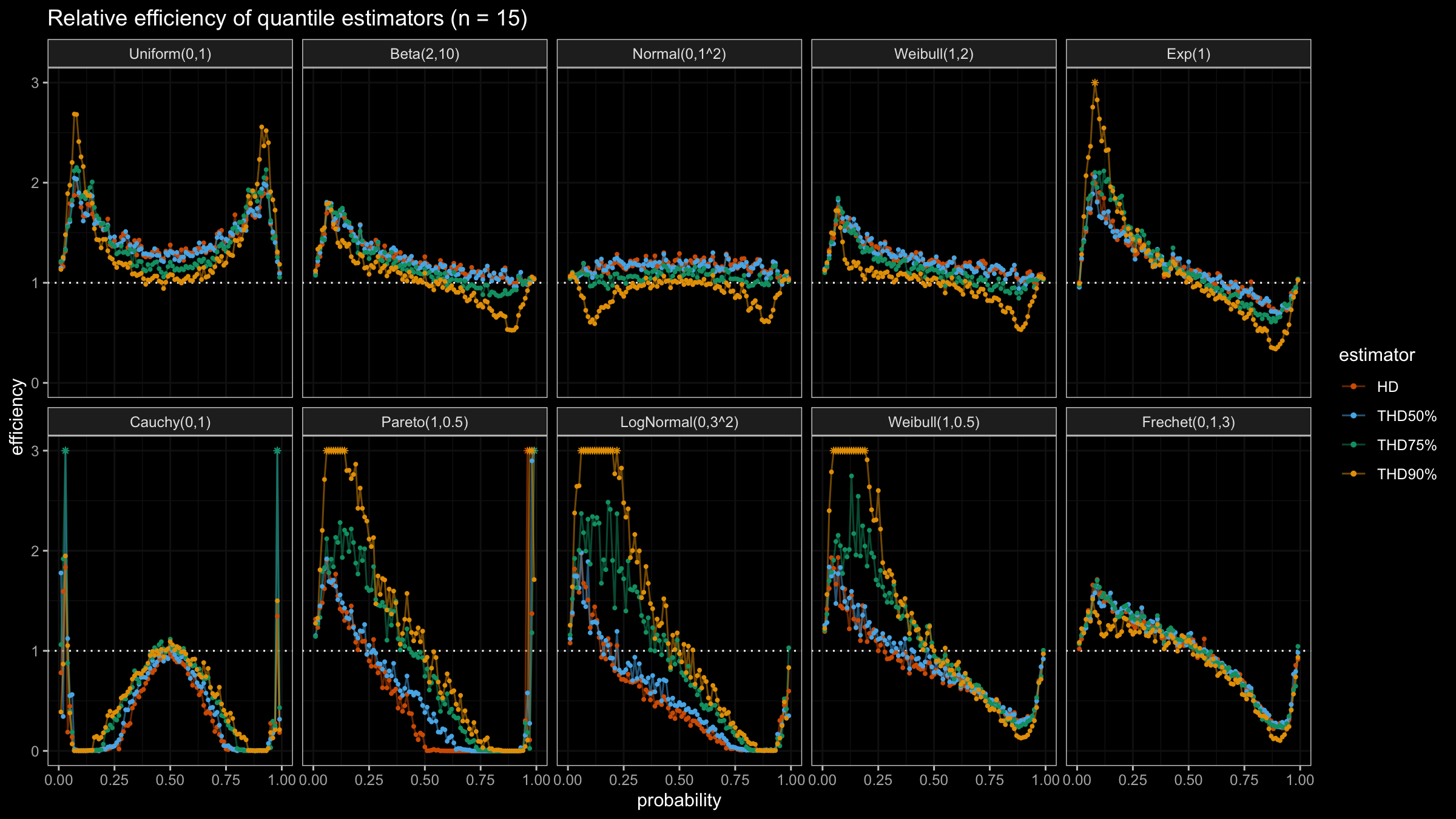
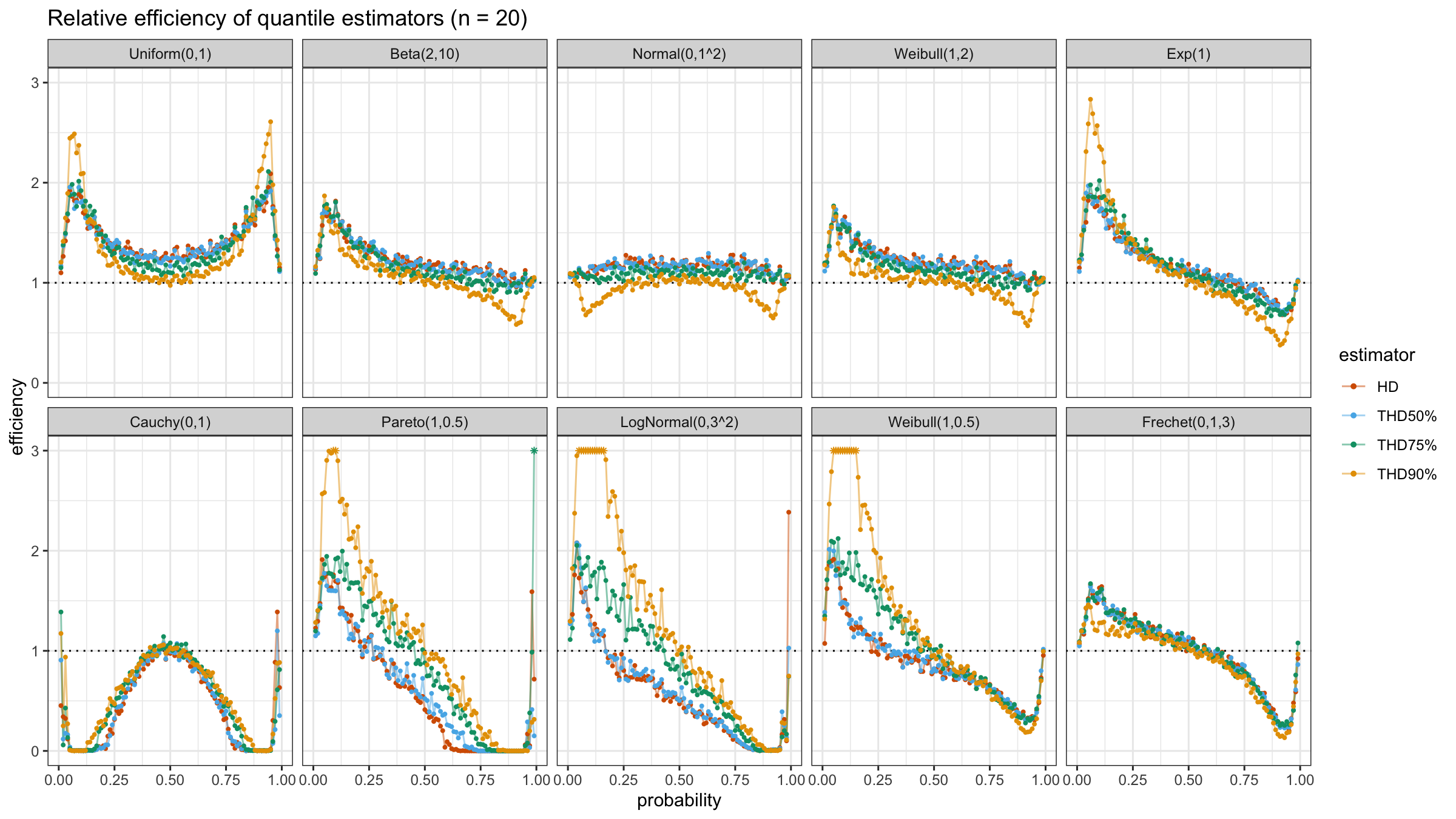
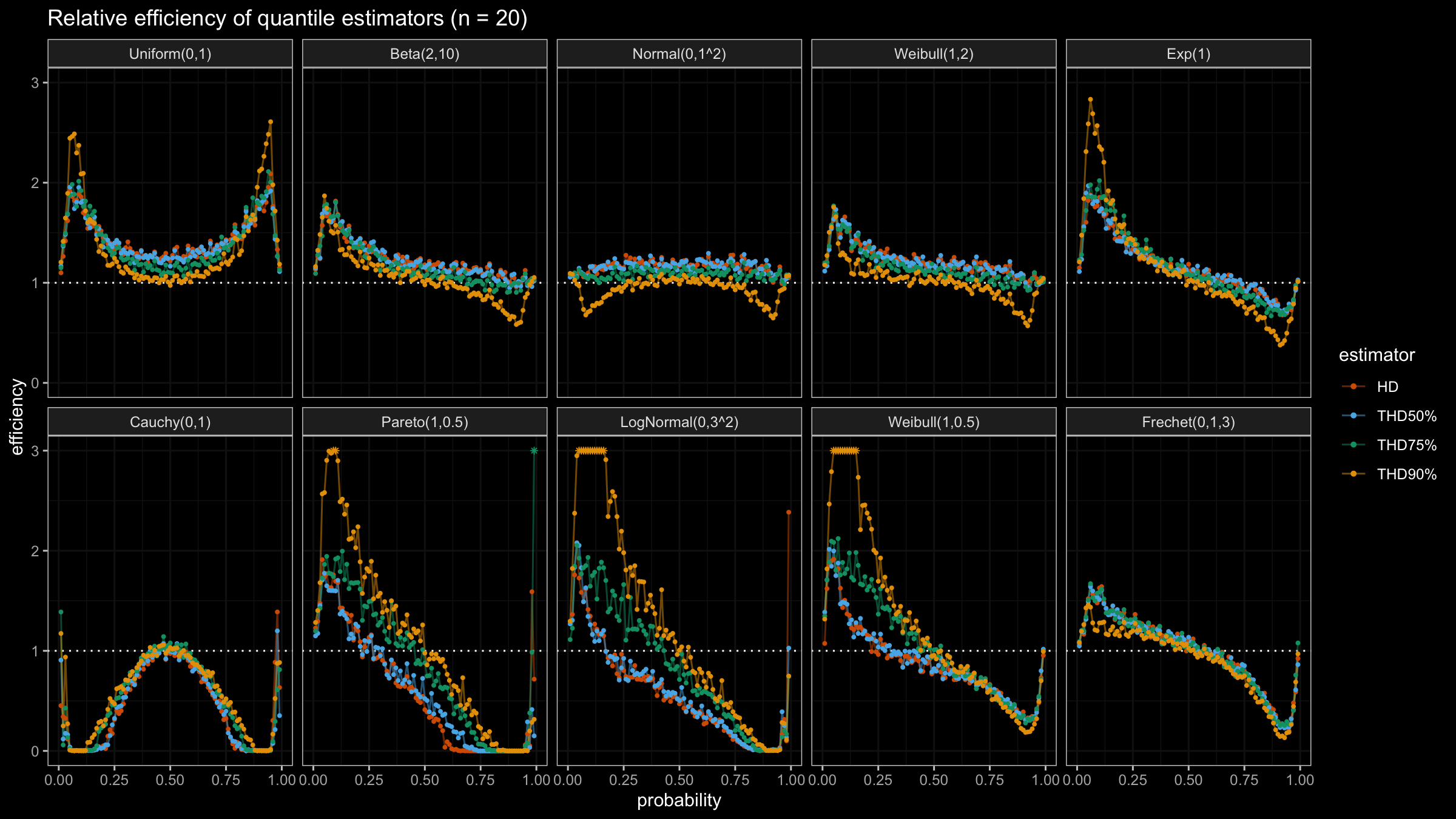
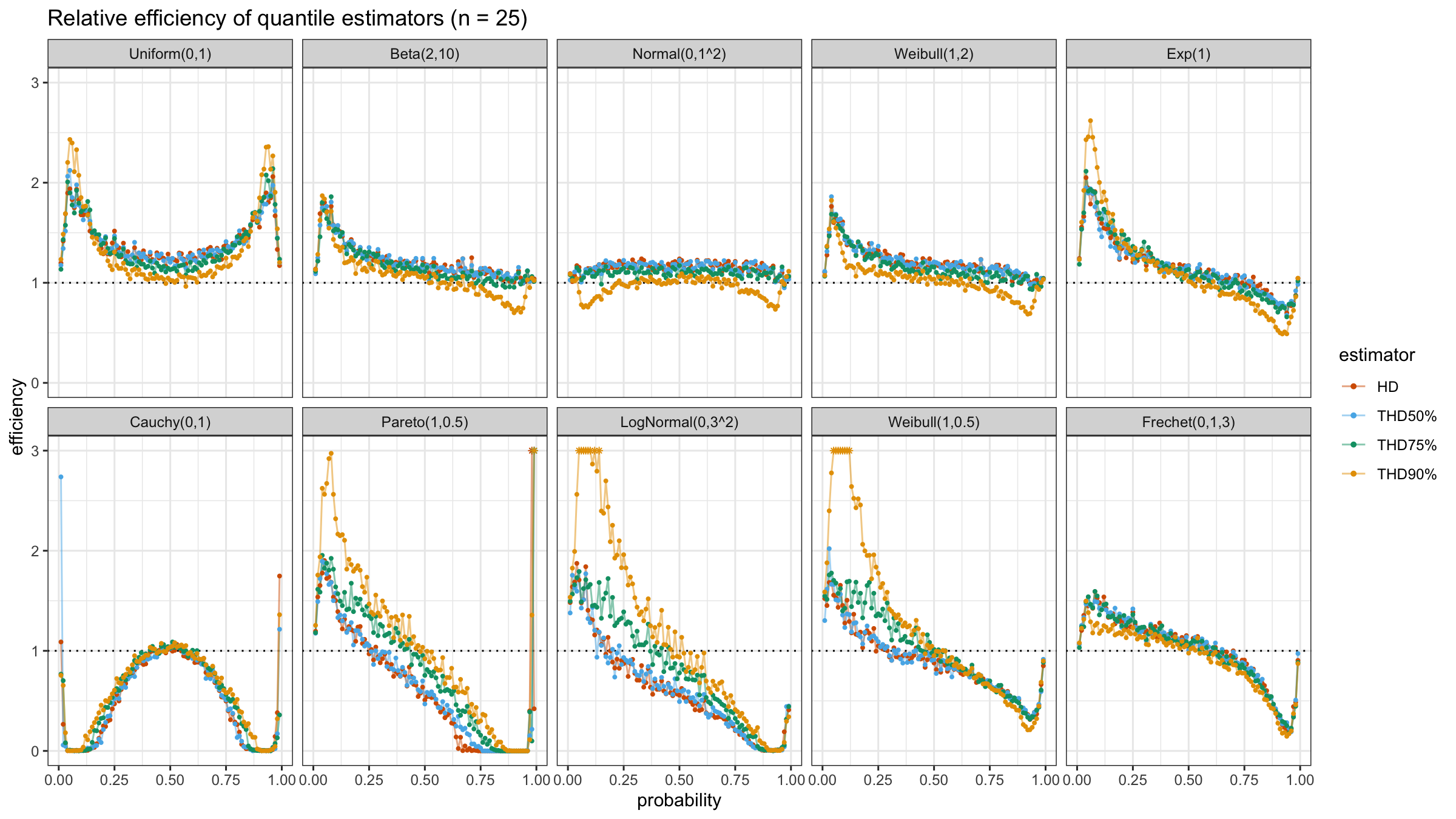
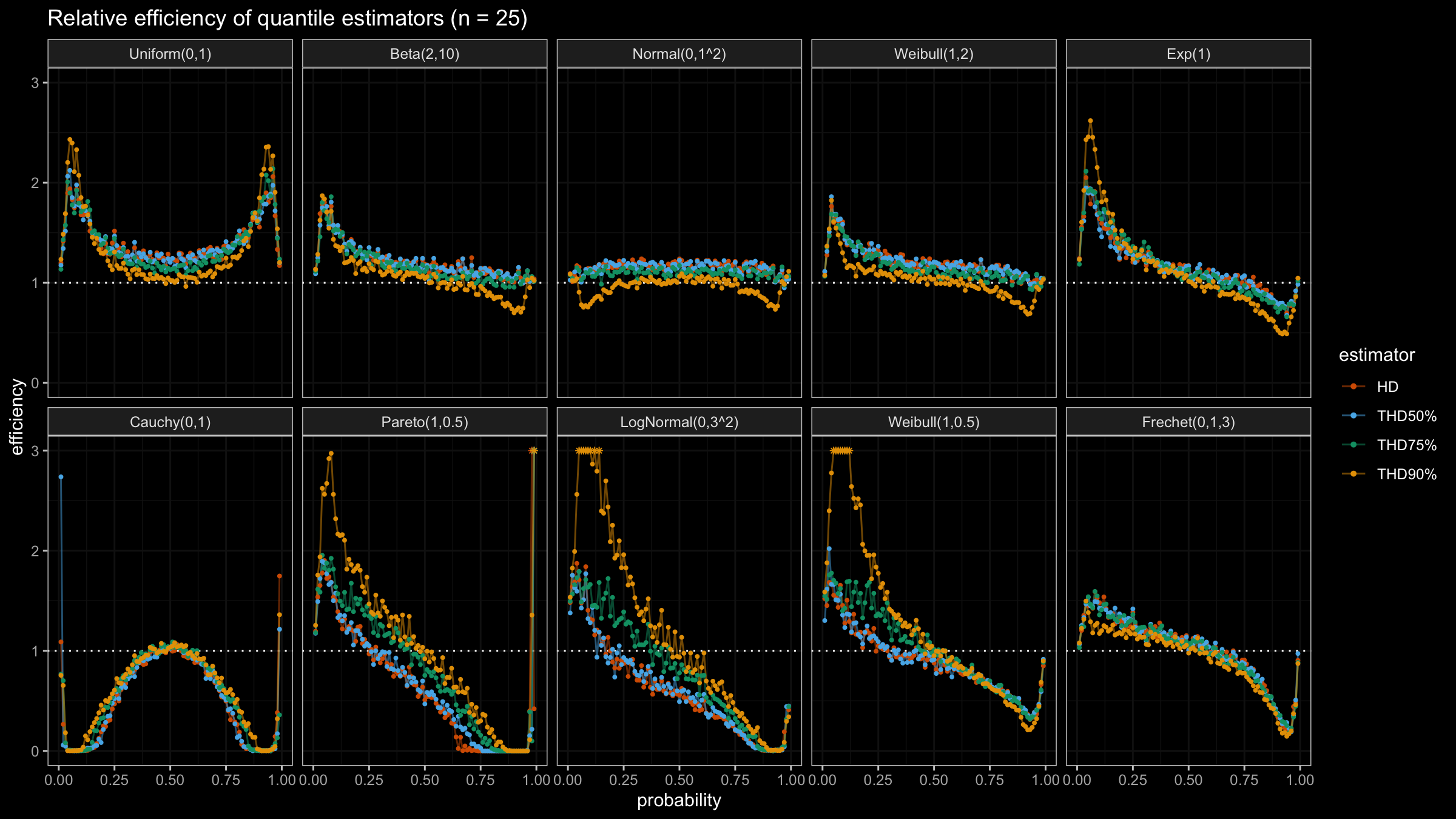
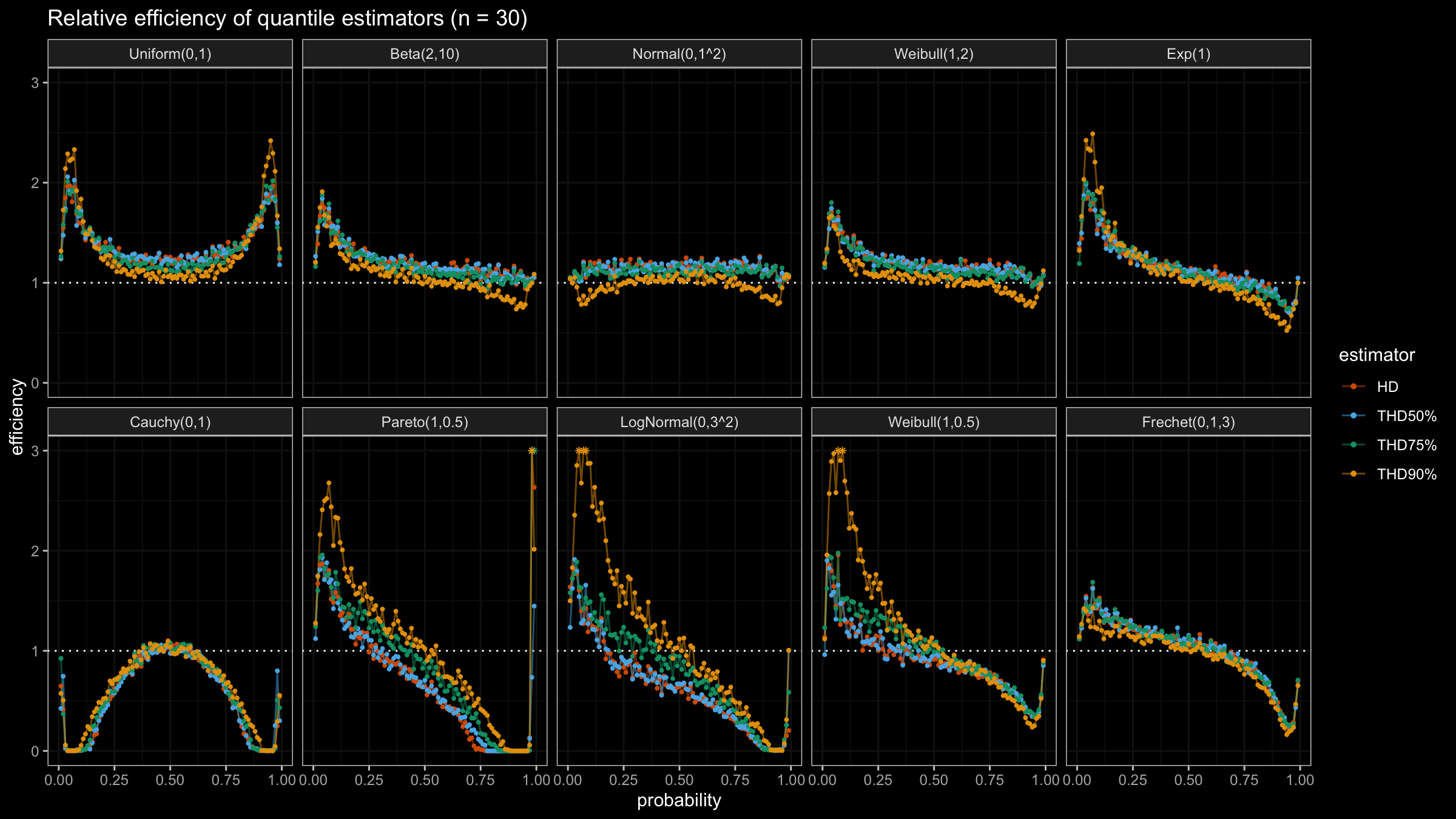
In this post, we are going to perform numerical simulations that check the statistical efficiency of the trimmed Harrell-Davis quantile estimator with different trimming percentages.

All posts from this series:

• Quantile estimators based on k order statistics, Part 1: Motivation (August 3, 2021)
• Quantile estimators based on k order statistics, Part 2: Extending Hyndman-Fan equations (August 10, 2021)
• Quantile estimators based on k order statistics, Part 3: Playing with the Beta function (August 17, 2021)
• Quantile estimators based on k order statistics, Part 4: Adopting trimmed Harrell-Davis quantile estimator (August 24, 2021)
• Quantile estimators based on k order statistics, Part 5: Improving trimmed Harrell-Davis quantile estimator (August 31, 2021)
• Quantile estimators based on k order statistics, Part 6: Continuous trimmed Harrell-Davis quantile estimator (September 7, 2021)
• Quantile estimators based on k order statistics, Part 7: Optimal threshold for the trimmed Harrell-Davis quantile estimator (September 14, 2021)
• Quantile estimators based on k order statistics, Part 8: Winsorized Harrell-Davis quantile estimator (September 21, 2021)

The approach

The primary idea is the same that we used in the previous post. The only difference is that now we set the width of the highest density interval as an estimator parameter.

Numerical simulations

We are going to take the same simulation setup that was declared in this post. Briefly speaking, we evaluate the classic MSE-based relative statistical efficiency of different quantile estimators on samples from different light-tailed and heavy-tailed distributions using the classic Hyndman-Fan Type 7 quantile estimator as the baseline.

The considered estimator based on T% trimming percentage is denoted as “THD-T%”.

Conclusion

It seems that ability to choose an arbitrary trimming percentage is a good step toward an optimal and flexible quantile estimator because it allows setting the breakdown point. Thus, we could easily control the trade-off between statistical efficiency and robustness.