Quantile estimators based on k order statistics, Part 7: Optimal threshold for the trimmed Harrell-Davis quantile estimator

In the previous post, we have obtained a nice quantile estimator. To be specific, we considered a trimmed modification of the Harrell-Davis quantile estimator based on the highest density interval of the given size. The interval size is a parameter that controls the trade-off between statistical efficiency and robustness. While it’s nice to have the ability to control this trade-off, there is also a need for the default value, which could be used as a starting point when we have neither estimator breakdown point requirements nor prior knowledge about distribution properties.

After a series of unsuccessful attempts, it seems that I have found an acceptable solution. We should build the new estimator based on \(\sqrt{n}/n\) order statistics. In this post, I’m going to briefly explain the idea behind the suggested estimator and share some numerical simulations that compare the proposed estimator and the classic Harrell-Davis quantile estimator.

All posts from this series:

• Quantile estimators based on k order statistics, Part 1: Motivation (August 3, 2021)
• Quantile estimators based on k order statistics, Part 2: Extending Hyndman-Fan equations (August 10, 2021)
• Quantile estimators based on k order statistics, Part 3: Playing with the Beta function (August 17, 2021)
• Quantile estimators based on k order statistics, Part 4: Adopting trimmed Harrell-Davis quantile estimator (August 24, 2021)
• Quantile estimators based on k order statistics, Part 5: Improving trimmed Harrell-Davis quantile estimator (August 31, 2021)
• Quantile estimators based on k order statistics, Part 6: Continuous trimmed Harrell-Davis quantile estimator (September 7, 2021)
• Quantile estimators based on k order statistics, Part 7: Optimal threshold for the trimmed Harrell-Davis quantile estimator (September 14, 2021)
• Quantile estimators based on k order statistics, Part 8: Winsorized Harrell-Davis quantile estimator (September 21, 2021)

The approach

The general idea is the same that was used in one of the previous posts. We express the estimation of the \(p^\textrm{th}\) quantile as a weighted sum of all order statistics:

\[\begin{gather*} q_p = \sum_{i=1}^{n} W_{i} \cdot x_i,\\ W_{i} = F(r_i) - F(l_i),\\ l_i = (i - 1) / n, \quad r_i = i / n, \end{gather*} \]

where \(F\) is a CDF function of a specific distribution. In the case of the Harrell-Davis quantile estimator, we use the Beta distribution. Thus, \(F\) could be expressed via regularized incomplete beta function \(I_x(\alpha, \beta)\):

\[F_{\operatorname{HD}}(u) = I_u(\alpha, \beta), \quad \alpha = (n+1)p, \quad \beta = (n+1)(1 - p). \]

In the case of the trimmed Harrell-Davis quantile estimator, we use only a part of the Beta distribution inside the \([L,\, R]\) window. Thus, \(F\) could be expressed as rescaled regularized incomplete beta function inside the given window:

\[F_{\operatorname{THD}}(u) = \left\{ \begin{array}{lcrcllr} 0 & \textrm{for} & & & u & < & L, \\ (F_{\operatorname{HD}}(u) - F_{\operatorname{HD}}(L)) / (F_{\operatorname{HD}}(R) - F_{\operatorname{HD}}(L)) & \textrm{for} & L & \leq & u & \leq & R, \\ 1 & \textrm{for} & R & < & u. & & \end{array} \right. \]

In the previous post, we discussed the idea of choosing \(L\) and \(R\) as a highest density interval of the given width \(R-L\). In this post, we are going to express the window size via the sample size \(n\) as follows:

\[R-L = \frac{\sqrt{n}}{n}. \]

If we don’t have any specific requirements for the estimator (e.g., the desired breakdown point) and we have no prior knowledge about distribution properties (e.g., the presence of a heavy tail), such an estimator looks like a good default option.

Numerical simulations

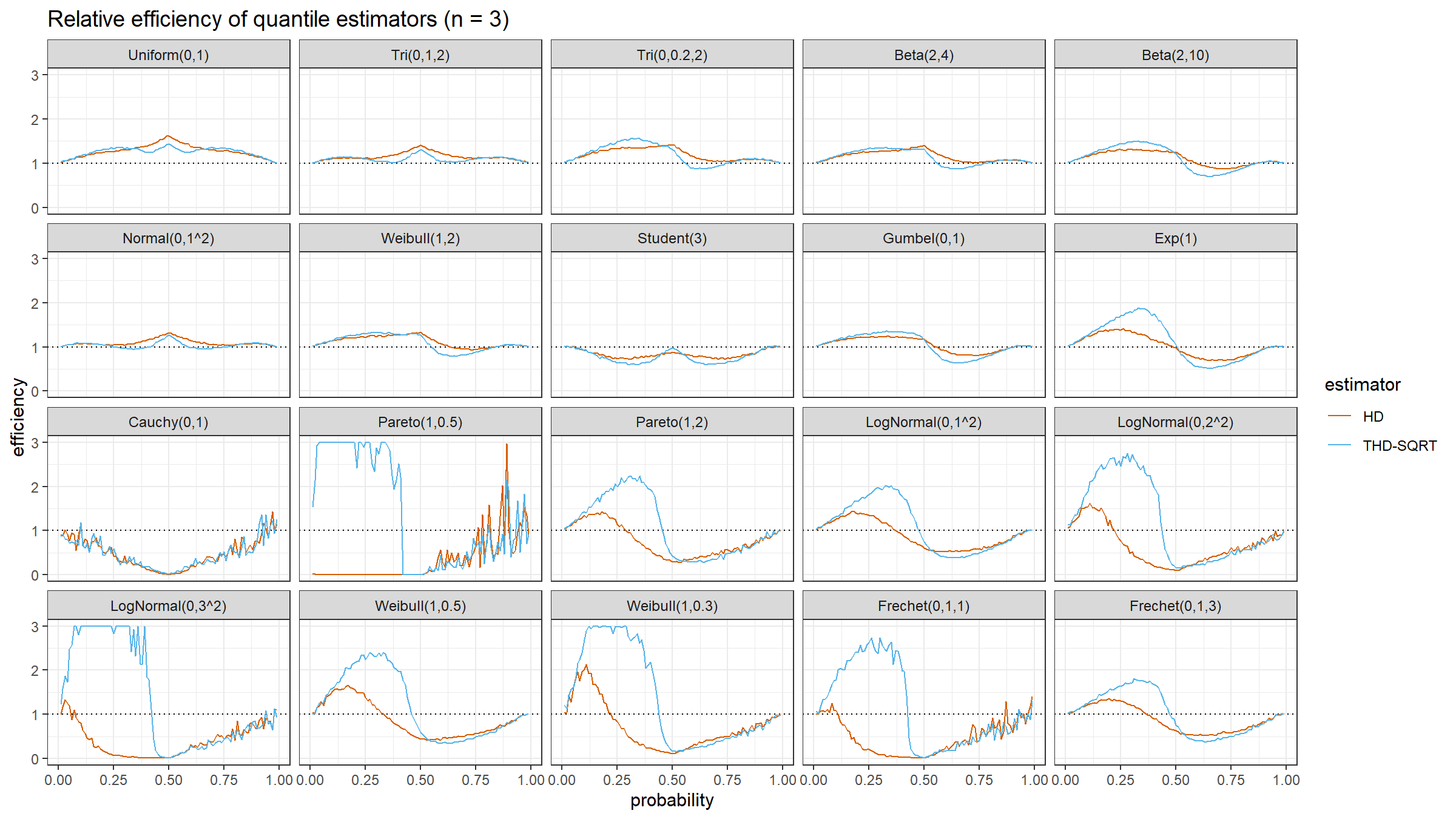
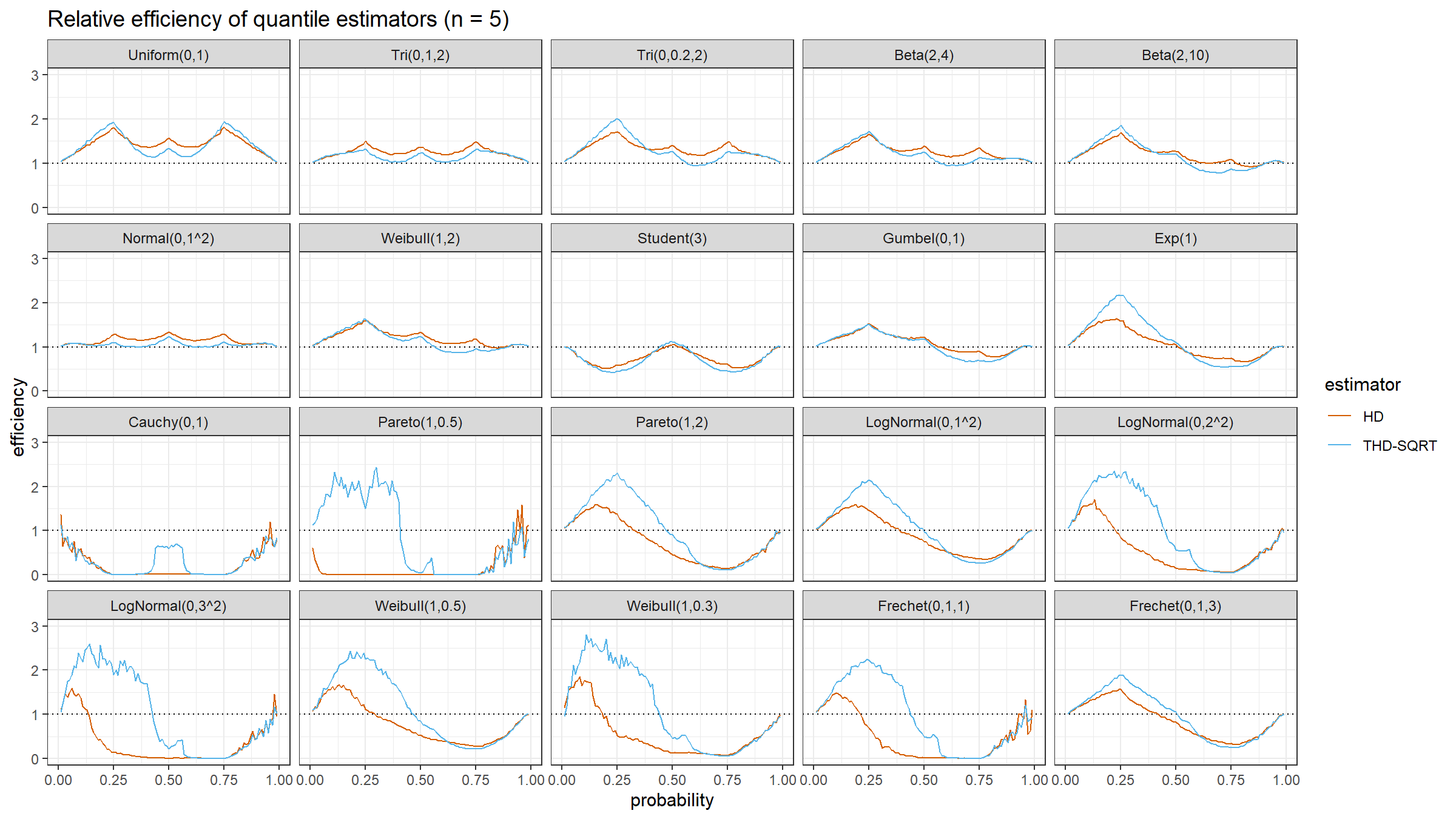
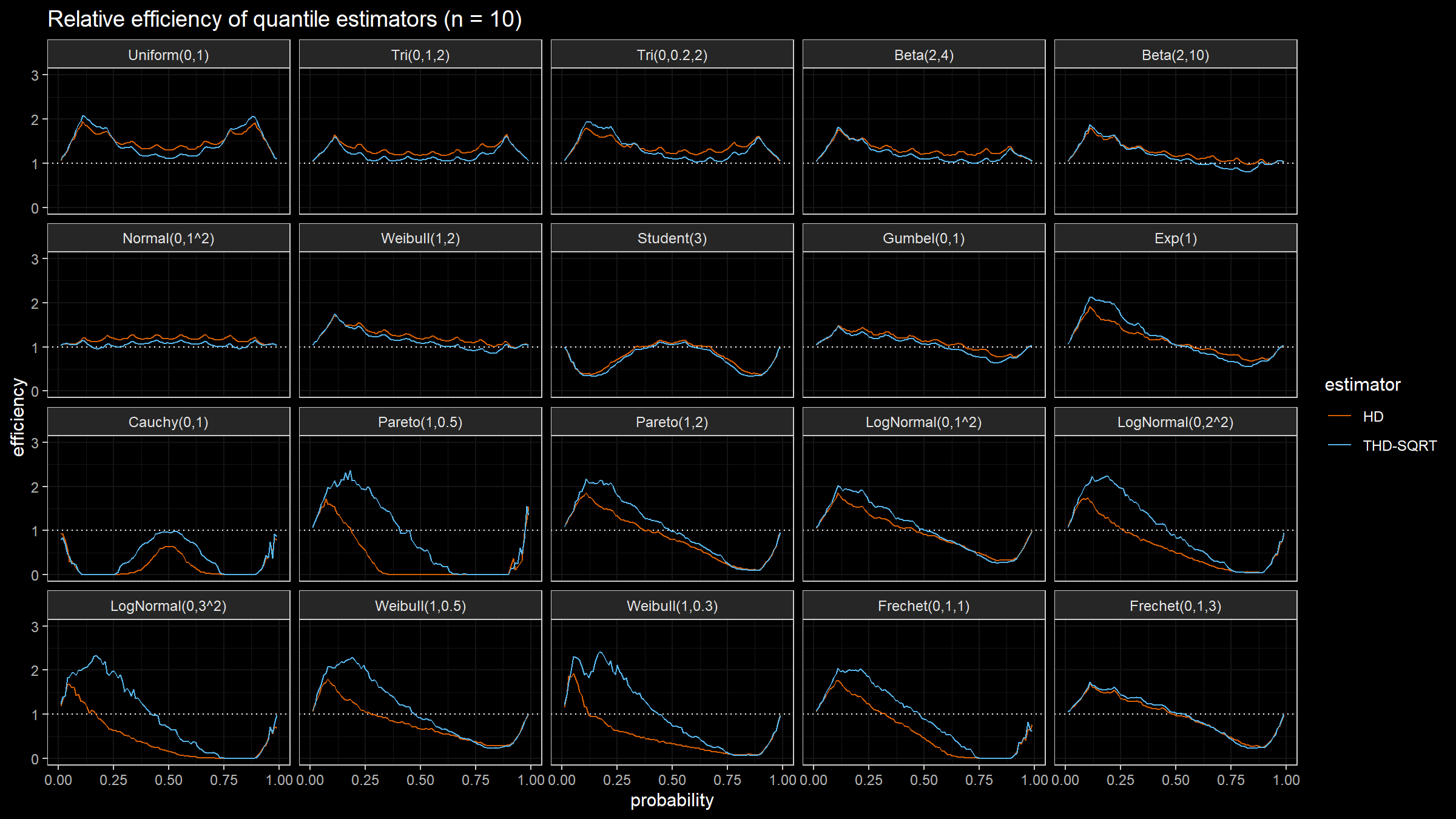
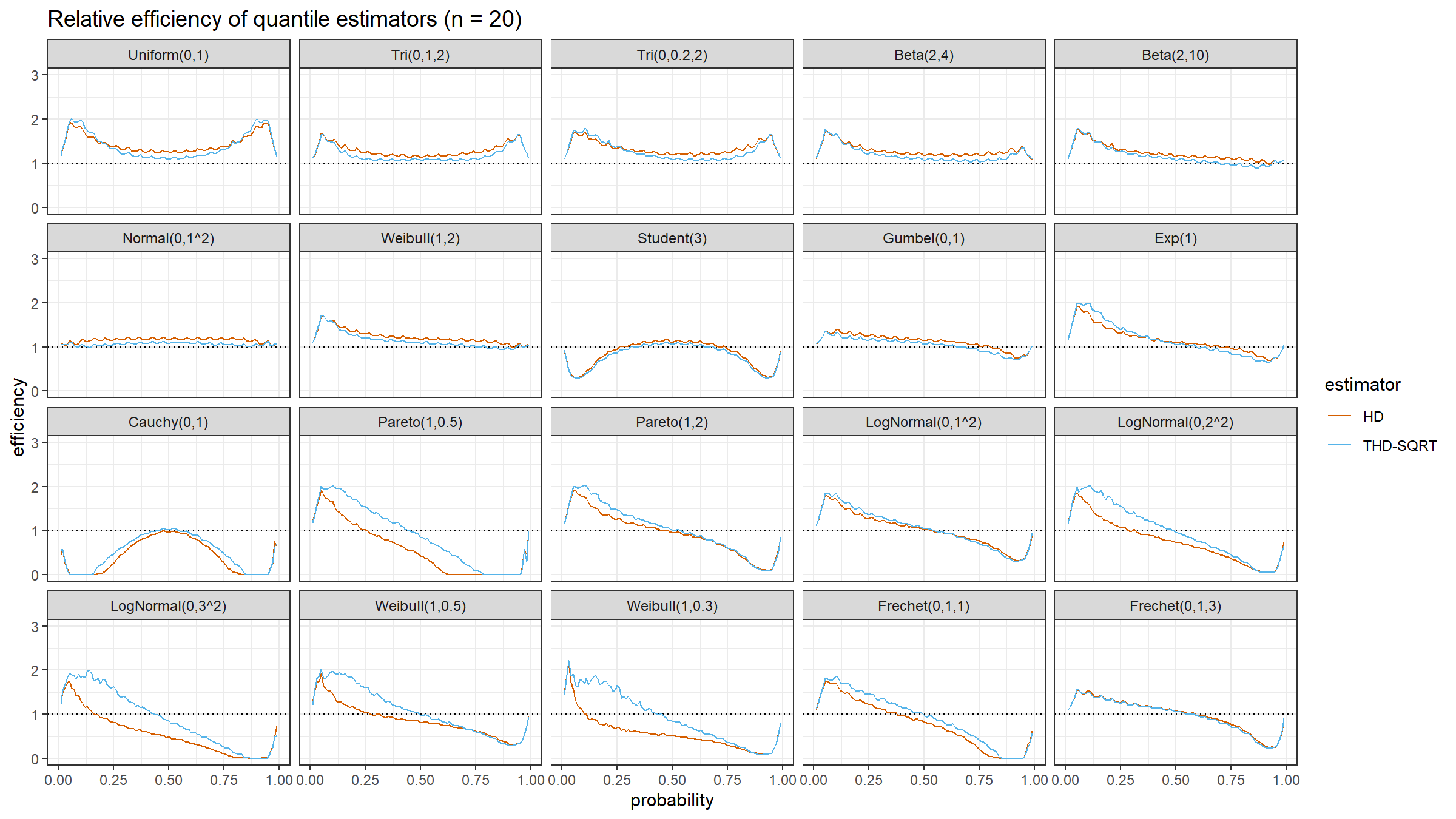
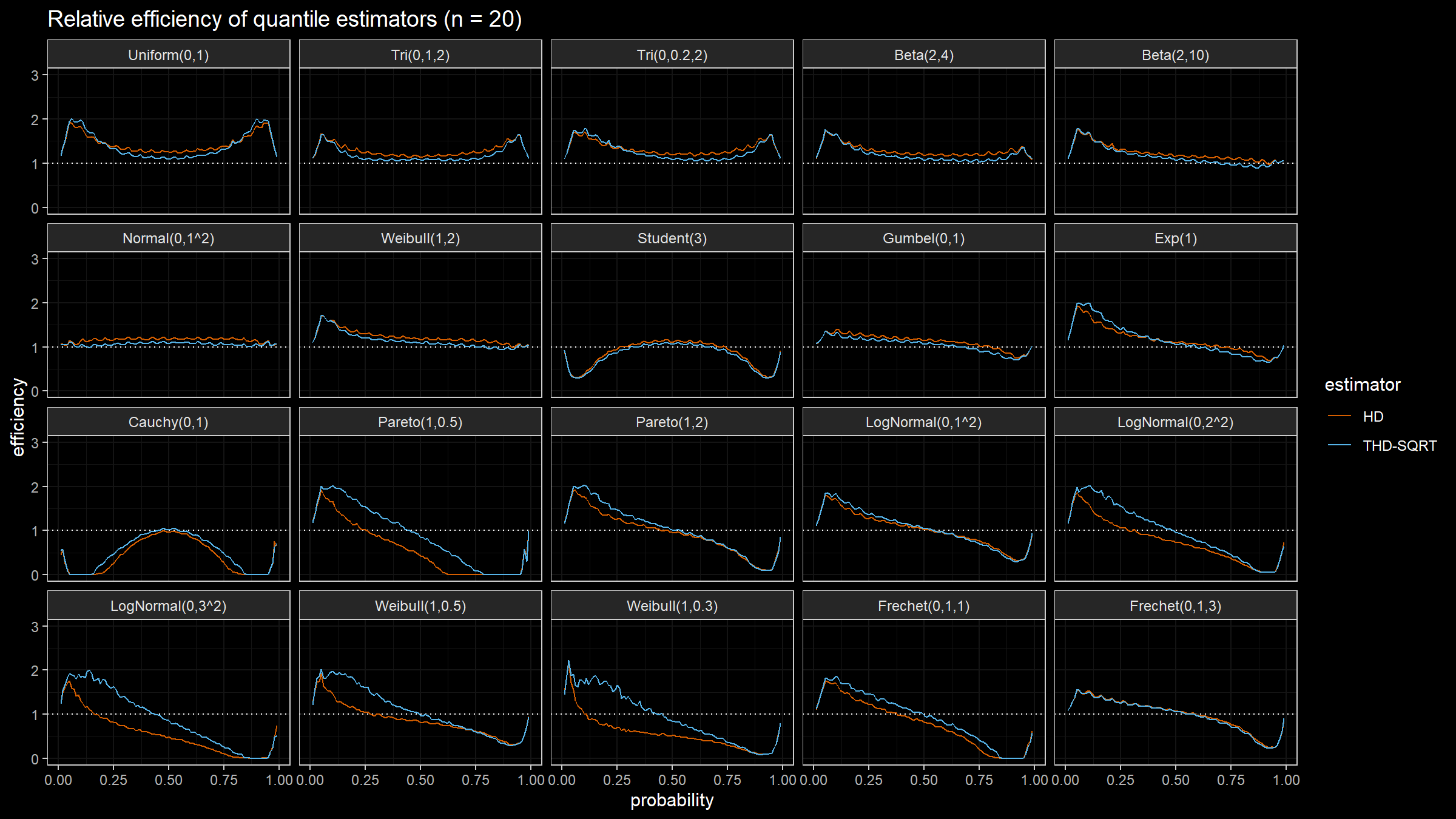
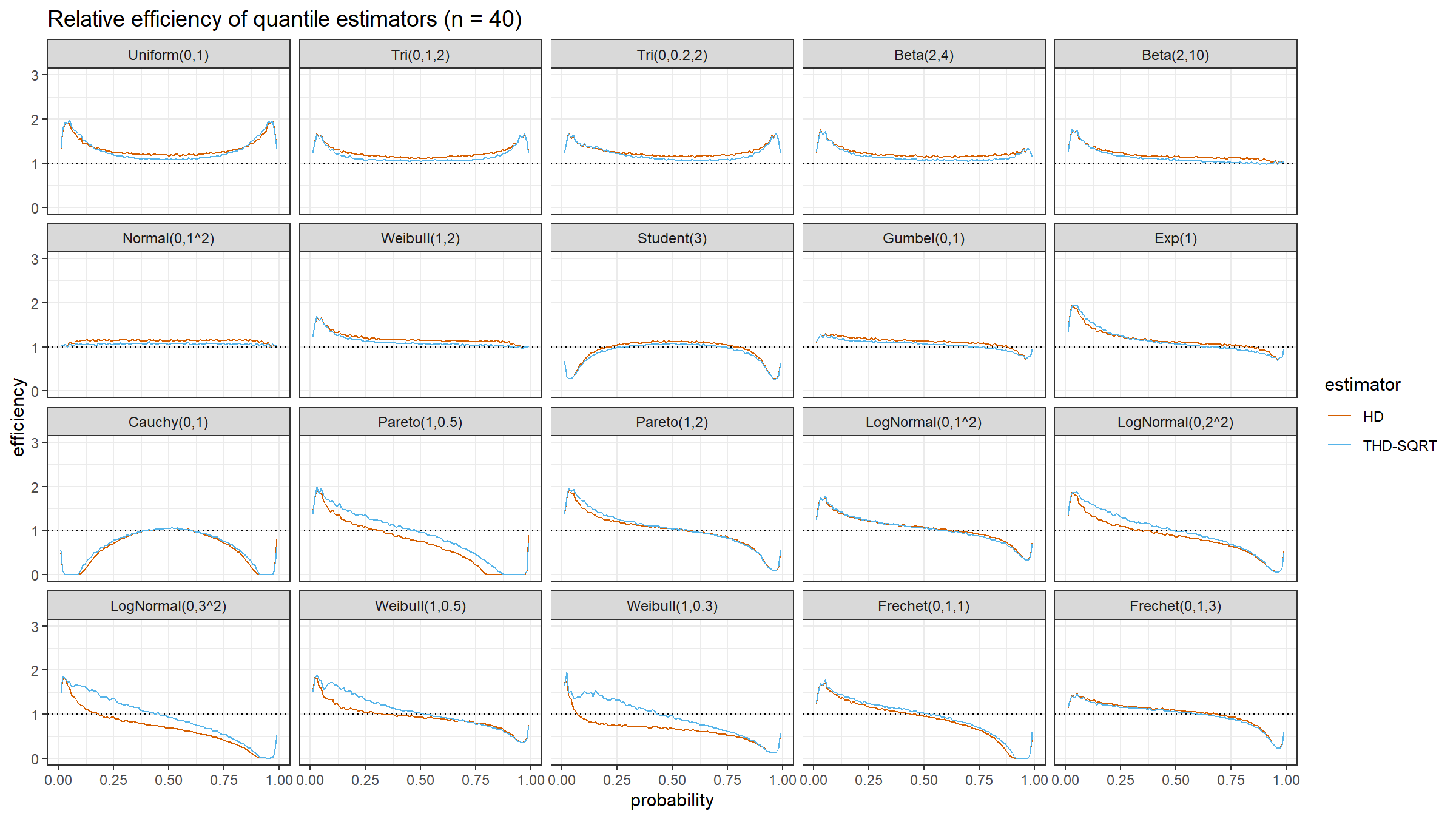
The relative efficiency value depends on five parameters:

• Target quantile estimator
• Baseline quantile estimator
• Estimated quantile \(p\)
• Sample size \(n\)
• Distribution

As target quantile estimators, we use:

• HD: Classic Harrell-Davis quantile estimator
• THD-SQRT: The described above trimmed modification of the Harrell-Davis quantile estimator based on highest density interval of size \(\sqrt{n}/n\).

The conventional baseline quantile estimator in such simulations is the traditional quantile estimator that is defined as a linear combination of two subsequent order statistics. To be more specific, we are going to use the Type 7 quantile estimator from the Hyndman-Fan classification or HF7. It can be expressed as follows (assuming one-based indexing):

\[Q_{HF7}(p) = x_{(\lfloor h \rfloor)}+(h-\lfloor h \rfloor)(x_{(\lfloor h \rfloor+1)})-x_{(\lfloor h \rfloor)},\quad h = (n-1)p+1. \]

Thus, we are going to estimate the relative efficiency of the trimmed Harrell-Davis quantile estimator with different percentage values against the traditional quantile estimator HF7. For the \(p^\textrm{th}\) quantile, the classic relative efficiency can be calculated as the ratio of the estimator mean squared errors (\(\textrm{MSE}\)):

\[\textrm{Efficiency}(p) = \dfrac{\textrm{MSE}(Q_{HF7}, p)}{\textrm{MSE}(Q_{\textrm{Target}}, p)} = \dfrac{\operatorname{E}[(Q_{HF7}(p) - \theta(p))^2]}{\operatorname{E}[(Q_{\textrm{Target}}(p) - \theta(p))^2]} \]

where \(\theta(p)\) is the true value of the \(p^\textrm{th}\) quantile. The \(\textrm{MSE}\) value depends on the sample size \(n\), so it should be calculated independently for each sample size value.

We are also going to use the following distributions:

• Uniform(0,1): Continuous uniform distribution; \(a = 0,\, b = 1\)
• Tri(0,1,2): Triangular distribution; \(a = 0,\, c = 1,\, b = 2\)
• Tri(0,0.2,2): Triangular distribution; \(a = 0,\, c = 0.2,\, b = 2\)
• Beta(2,4): Beta distribution; \(\alpha = 2,\, \beta = 4\)
• Beta(2,10): Beta distribution; \(\alpha = 2,\, \beta = 10\)
• Normal(0,1^2): Standard normal distribution; \(\mu = 0,\, \sigma = 1\)
• Weibull(1,2): Weibull distribution; \(\lambda = 1\;\textrm{(scale)},\, k = 2\;\textrm{(shape)}\)
• Student(3): Student distribution; \(\nu = 3\;\textrm{(degrees of freedom)}\)
• Gumbel(0,1): Gumbel distribution; \(\mu = 0\;\textrm{(location)},\, \beta = 1\;\textrm{(scale)}\)
• Exp(1): Exponential distribution; \(\lambda = 1\;\textrm{(rate)}\)
• Cauchy(0,1): Standard Cauchy distribution; \(x_0 = 0\;\textrm{(location)},\,\gamma = 1\;\textrm{(scale)}\)
• Pareto(1,0.5): Pareto distribution; \(x_m = 1\;\textrm{(scale)},\, \alpha = 0.5\;\textrm{(shape)}\)
• Pareto(1,2): Pareto distribution; \(x_m = 1\;\textrm{(scale)},\, \alpha = 2\;\textrm{(shape)}\)
• LogNormal(0,1^2): Log-normal distribution; \(\mu = 0, \sigma = 1\)
• LogNormal(0,2^2): Log-normal distribution; \(\mu = 0, \sigma = 2\)
• LogNormal(0,3^2): Log-normal distribution; \(\mu = 0, \sigma = 3\)
• Weibull(1,0.5): Weibull distribution; \(\lambda = 1\;\textrm{(scale)},\, k = 0.5\;\textrm{(shape)}\)
• Weibull(1,0.3): Weibull distribution; \(\lambda = 1\;\textrm{(scale)},\, k = 0.3\;\textrm{(shape)}\)
• Frechet(0,1,1): Frechet distribution; \(m=0\;\textrm{(location)},\, s = 1\;\textrm{(scale)},\, \alpha = 1\;\textrm{(shape)}\)
• Frechet(0,1,3): Frechet distribution; \(m=0\;\textrm{(location)},\, s = 1\;\textrm{(scale)},\, \alpha = 3\;\textrm{(shape)}\)

Simulation Results

Conclusion

The trimmed modification of the Harrell-Davis quantile estimator based on the highest density interval of size \(\sqrt{n}/n\) looks like a good option for a “default” quantile estimator for different applications. In the next blog posts, we will continue to evaluate different options of the suggested approach.