Lowland multimodality detection and robustness

We continue exploring various corner cases for the Lowland multimodality detection. In this post, we consider an example that illustrates the usefulness of THDQE.

QRDE-HD is based on the Harrell-Davis quantile estimator (see harrell1982), which is not robust. It works fine in “simple” cases, but the estimation may be distorted in the presence of extreme outliers or extreme distances between modes. This problem can be mitigated using the trimmed modification of the Harrell-Davis quantile estimator (THDQE), which is described in akinshin2022thdqe. As proposed in the paper, we use the length of the target interval equal to $\sqrt{n}$ for the trimming procedure. We refer to such an estimator as THDQE-SQRT.

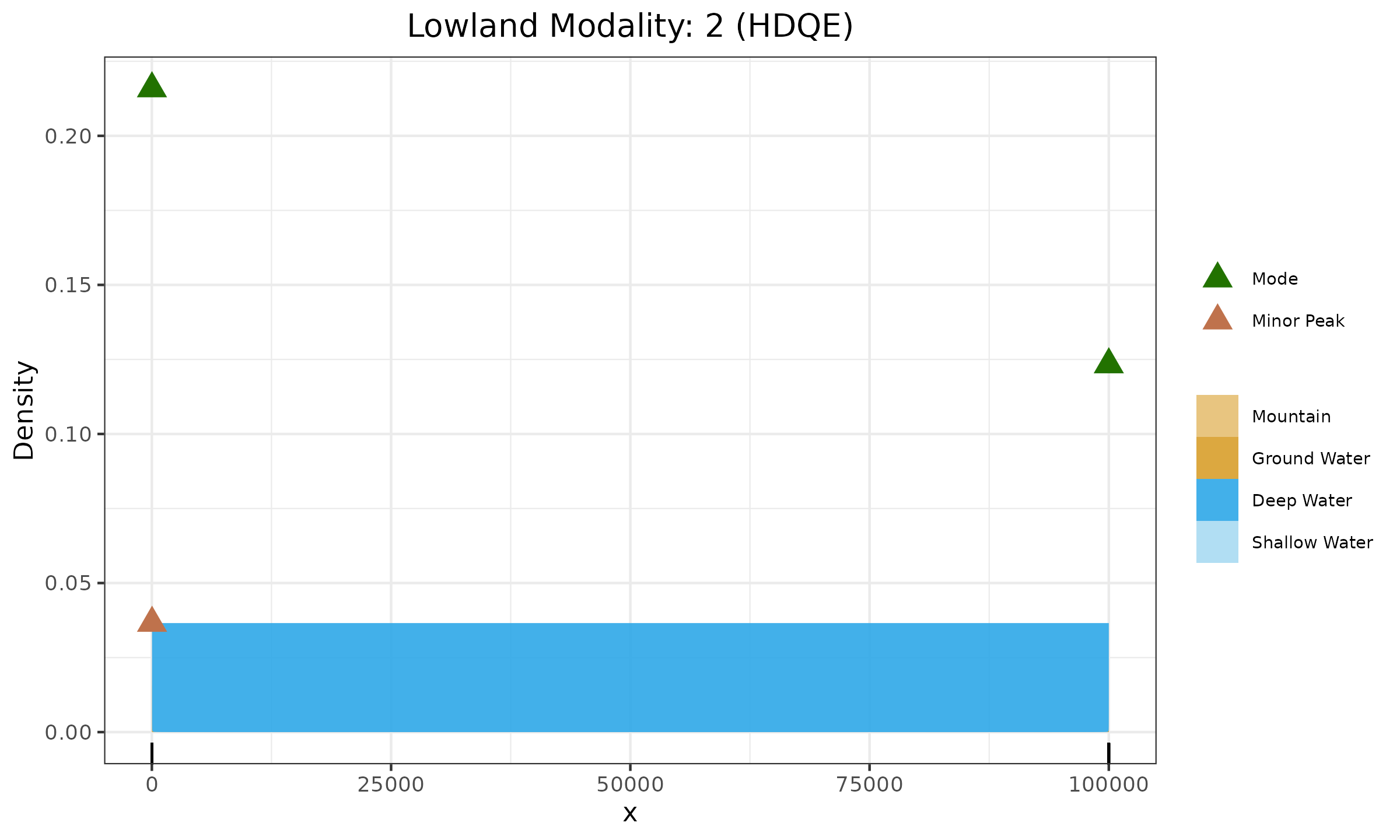
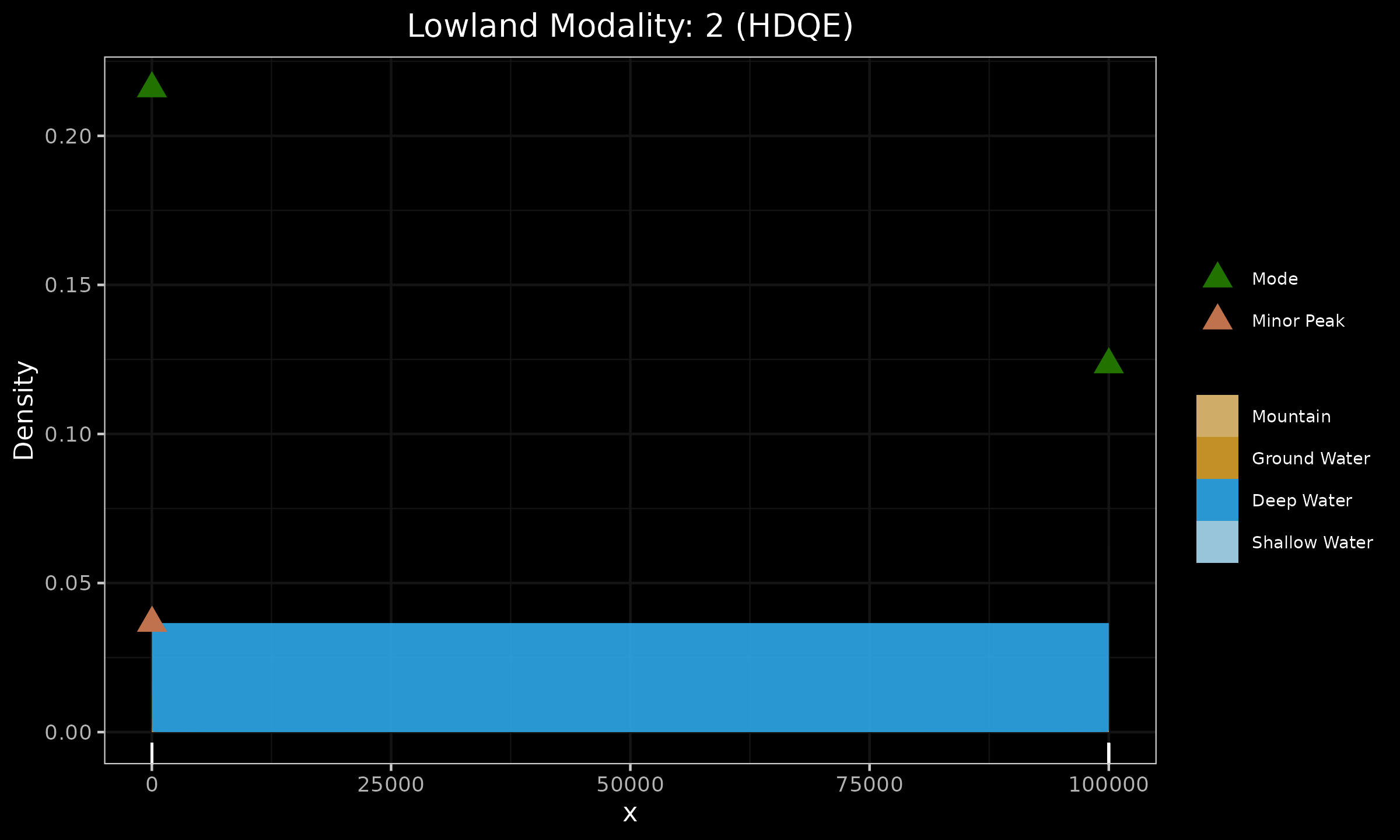
Let us review an example, in which the usage of THDQE-SQRT helps to improve the detection results. We consider a sample with $30$ elements from $\mathcal{N}(10, 1)$, $30$ elements from $\mathcal{N}(20, 1)$, and $30$ elements from $\mathcal{N}(10^5, 1)$. We may expect to detect three modes. However, as shown in the below figure, the first two modes were merged due to the impact of the third mode and the lack of robustness of HDQE.

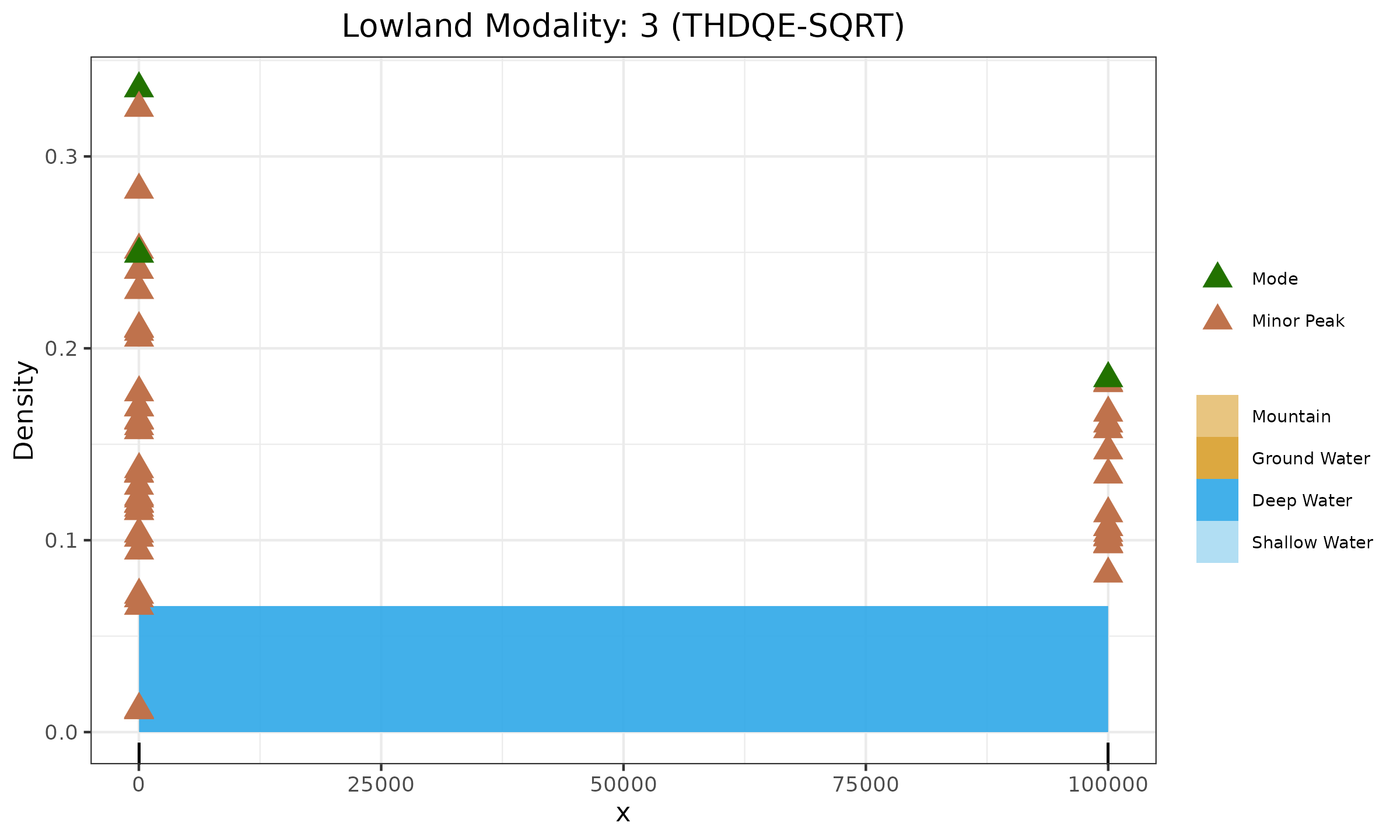
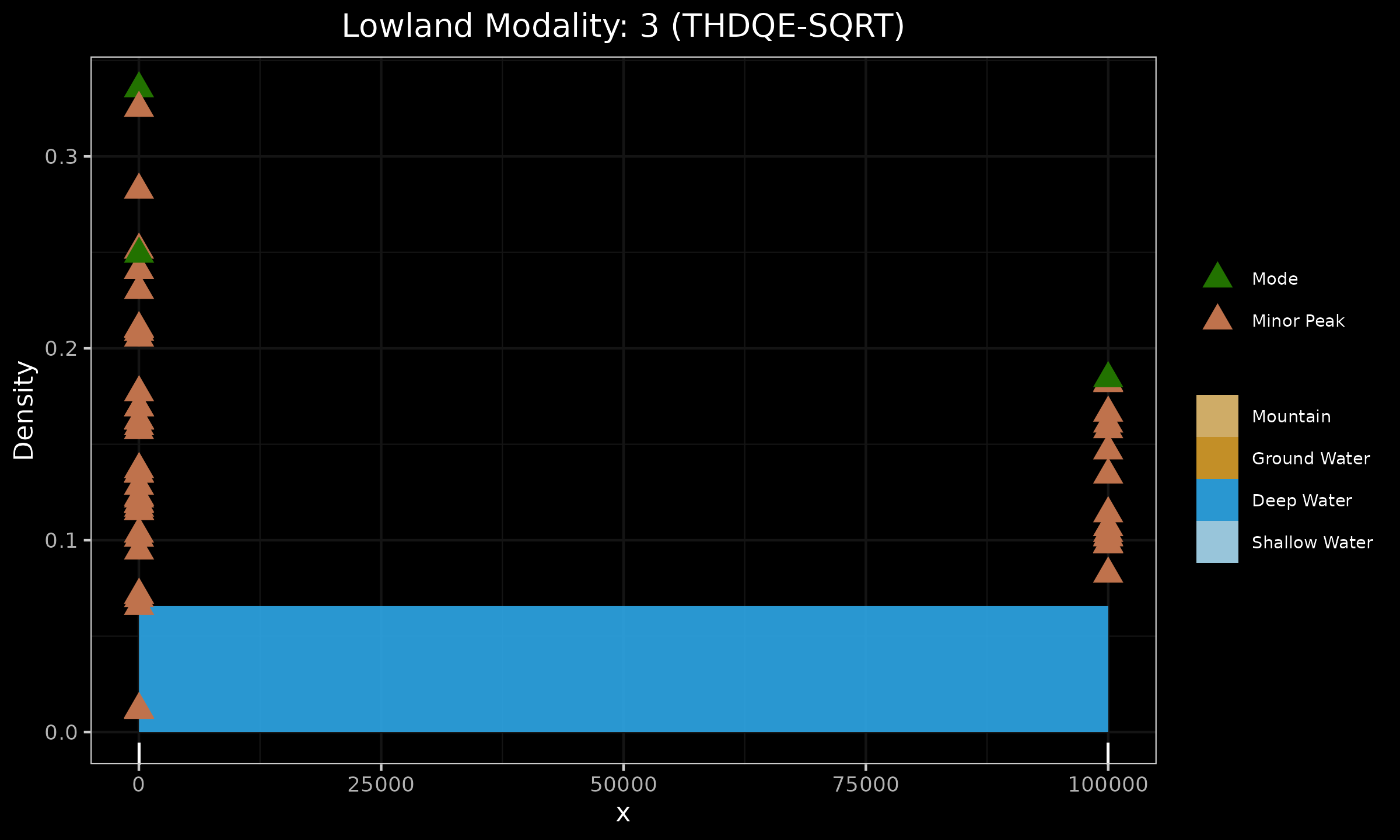
In the next figure, three modes are correctly detected thanks to the usage of THDQE-SQRT.

When extreme outliers are expected, it is recommended to prefer THDQE over HDQE for the lowland multimodality detection.