Lowland multimodality detection and weighted samples

We continue exploring various use cases of the Lowland multimodality detection. In this post, we will consider a brief example of using weighted samples.

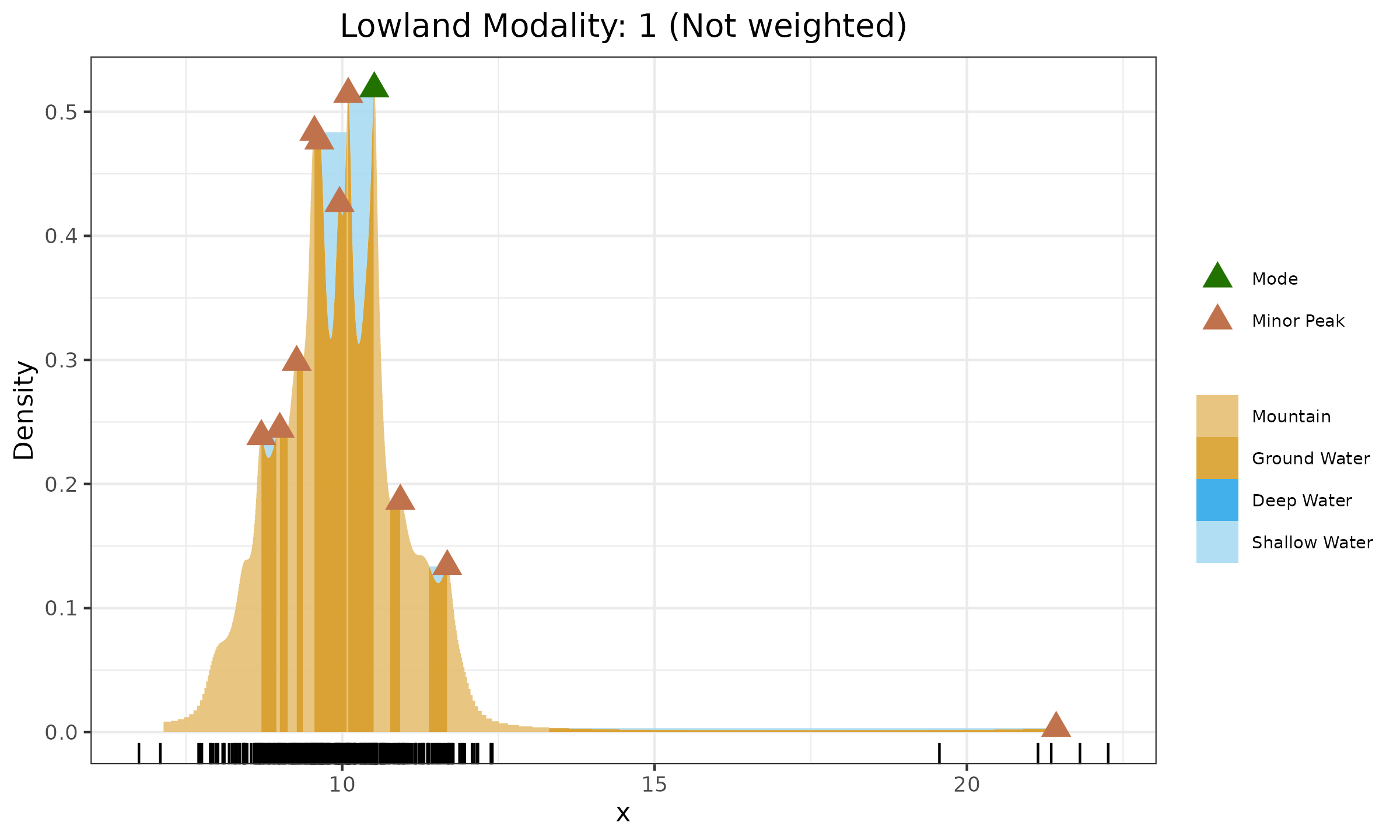
Let us consider a sample of $395$ elements from $\mathcal{N}(10, 1)$ and 5 elements from $\mathcal{N}(20, 1)$. In the first Figure, it is shown that we failed to detect the second mode since the number of data points is not sufficient enough to perceive it as a separate mode rather than a few outliers.

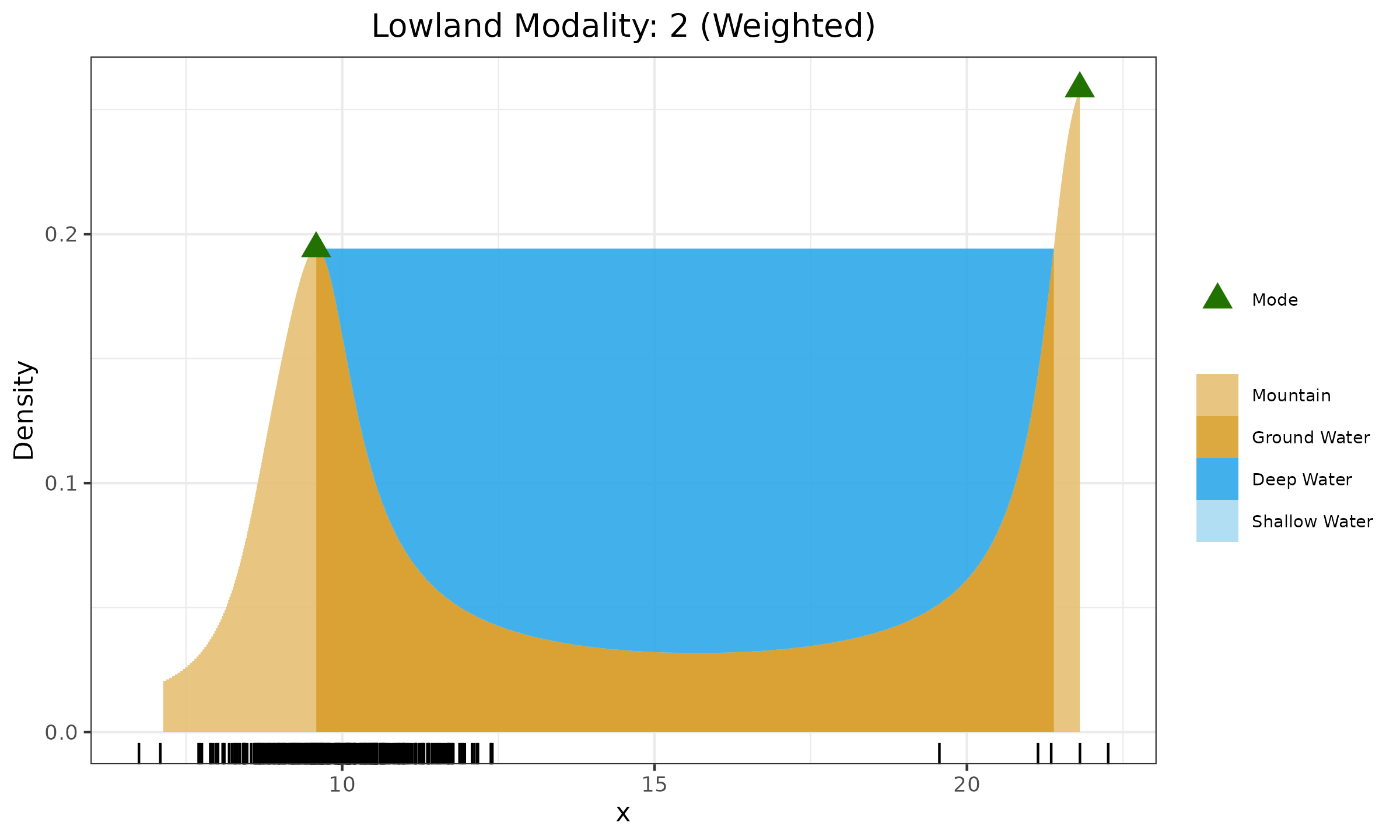
Now, we say that both parts of the sample came from equal parts of the underlying distribution. The only difference is that we were able to collect 395 measurements for the first part, while only 5 measurements for the second part are available. If we believe that these parts are equally presented in the population, we can replace the sample by assigning weights to the elements. The first $395$ elements get the weight of $1/395$, and the last $5$ elements get the weight of $1/5$. In the second Figure, we can see that now we correctly detect two equal modes thanks to the usage of weights.