Multimodal distributions and effect size

When we want to express the difference between two samples or distributions, a popular measure family is the effect sizes based on differences between means (difference family). When the normality assumption is satisfied, this approach works well thanks to classic measures of effect size like Cohen’s d, Glass’ Δ, or Hedges’ g. With slight deviations from normality, robust alternatives may be considered. To build such a measure, it’s enough to upgrade classic measures by replacing the sample mean with a robust measure of central tendency and replacing the standard deviation with a robust measure of dispersion. However, it might not be enough in the case of large deviations from normality. In this post, I briefly discuss the problem of effect size evaluation in the context of multimodal distributions.

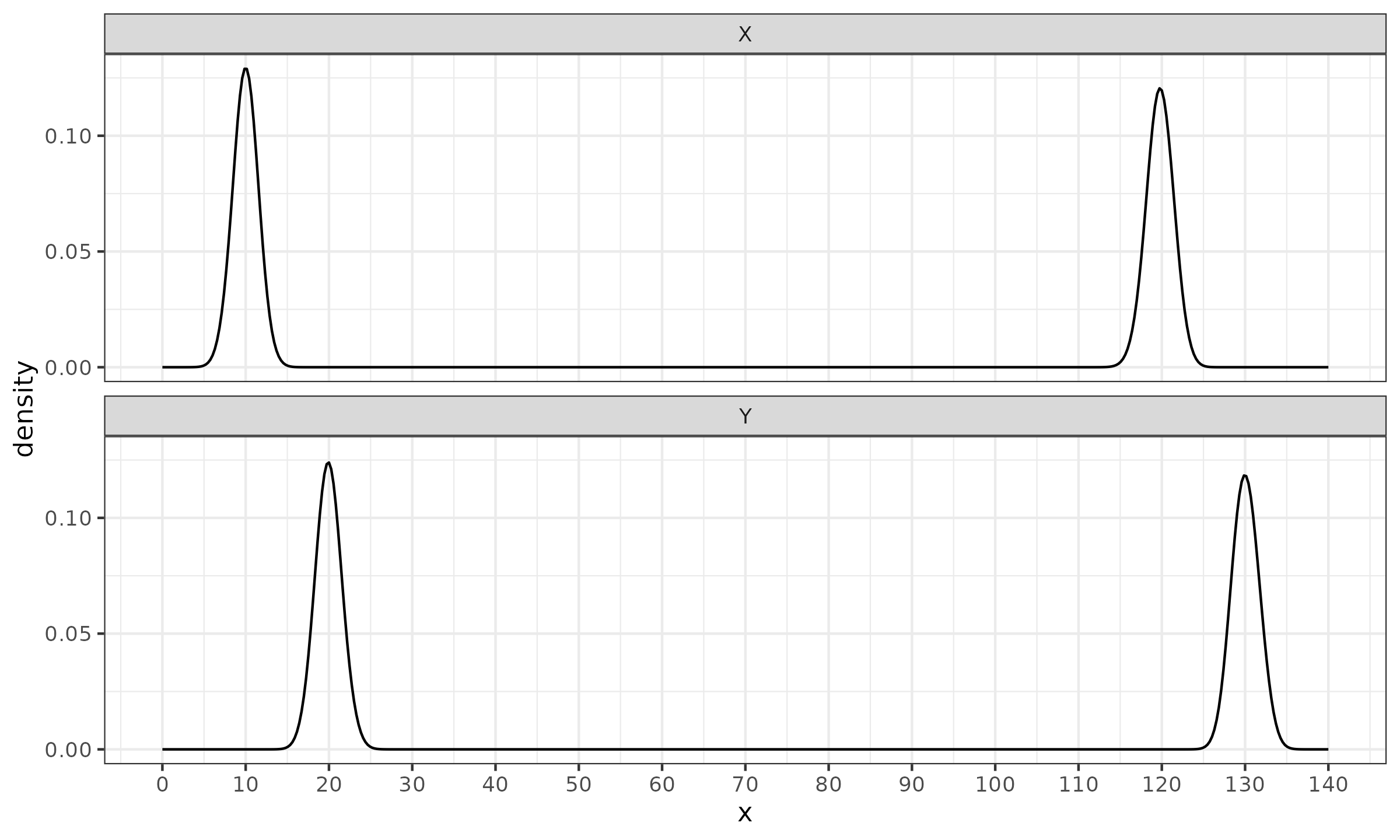
Let us consider two multimodal distributions given by the following density plots:

Both distributions have the same shape of a perfect bimodal distribution that is formed by two normal distributions. The $Y$ distribution is a shifted version of the $X$ distribution. All the classic measures of dispersion (including robust measures) are heavily affected by the distance between modes. For example, in our case, the standard deviation and the median absolute deviation are about $\approx 55$. Meanwhile, the absolute shift between distributions is $10$. If we estimate the effect size as the shift divided by the dispersion, we get $10 / 55 \approx 0.18$, which is considered a small effect.

However, the actual effect is quite significant. Let us compare only the left modes of the given distributions. The true standard deviation (and the corresponding median absolute deviation) is $1$, while the shift value remains $10$. This gives us the effect size of $10 / 1 = 10$, which is considered an enormous effect size. Unfortunately, multimodality hides the true scale of the effect.

So, which answer is correct? As usual, it depends on our research goals: we should clearly define why we need the effect size and what kind of decisions we are going to make based on the obtained measurements. Once the goals are established, we can speculate on which measure of effect size to choose. However, as a rule of thumb, I recommend detecting multimodality phenomena (e.g., using the lowland multimodality detector) and analyzing the individual modes separately. This approach can be tedious (especially in the case of non-trivial mode configuration), but it helps to achieve more reliable and trustworthy results.