Edgeworth expansion for the Mann-Whitney U test, Part 2: increased accuracy
In the previous post, we showed how the Edgeworth expansion can improve the accuracy of obtained p-values in the Mann-Whitney U test. However, we considered only the Edgeworth expansion to terms of order $1/m$. In this post, we explore how to improve the accuracyk of this approach using the Edgeworth expansion to terms of order $1/m^2$.
Extended Edgeworth approximation
In this post, we follow the approach from [Fix1955] to get various Edgeworth expansions for the Mann-Whitney U distribution. We denote the previously considered expansion by $p_{E3}$, and the extended one by $p_{E7}$. These expansions are defined as follows:
$$ p_{E3}(z) = \Phi(z) + e^{(3)} \varphi^{(3)}(z), $$$$ p_{E7}(z) = \Phi(z) + e^{(3)} \varphi^{(3)}(z) + e^{(5)} \varphi^{(5)}(z) + e^{(7)} \varphi^{(7)}(z). $$The Edgeworth coefficients $e^{(3)}$, $e^{(5)}$, $e^{(7)}$ are given by
$$ e^{(3)} = \frac{1}{4!}\left( \frac{\mu_4}{\mu_2^2} - 3 \right),\quad e^{(5)} = \frac{1}{6!}\left( \frac{\mu_6}{\mu_2^3} - 15\frac{\mu_4}{\mu_2^2} + 30 \right),\quad e^{(7)} = \frac{35}{8!}\left( \frac{\mu_4}{\mu_2^2} - 3 \right)^2, $$where $\mu_k$ is the $k^\textrm{th}$ central moment of the Mann-Whitney U distribution:
$$ \mu_2 = \frac{nm(n+m+1)}{12}, $$$$ \mu_4 = \frac{mn(m+n+1)}{240} \bigl( 5(m^2 n + m n^2) - 2(m^2 + n^2) + 3mn - (2m + n) \bigr), $$$$ \begin{split} \mu_6 = \frac{mn(m+n+1)}{4032} \bigl( 35m^2 n^2 (m^2 + n^2) + 70 m^3 n^3 - 42 mn (m^3 + n^3) - 14 m^2 n^2 (m + n) +\\ + 16 (m^4 + n^4) - 52 mn (m^2 + n^2) - 43 m^2 n^2 + 32 (m^3 + n^3) +\\ + 14 mn (m + n) + 8 (m^2 + n^2) + 16 mn - 8 (m + n) \bigr). \end{split} $$The terms $\varphi^{(3)}$, $\varphi^{(5)}$, $\varphi^{(7)}$ are the derivatives of the standard normal distribution density function $\varphi$. They can be expressed using the Hermite polynomials:
$$ \varphi^{(k)}(z) = -\varphi(z) H_k(z), $$$$ H_3(z) = z^3 - 3z, $$$$ H_5(z) = z^5 - 10z^3 + 15z, $$$$ H_7(z) = z^7 - 21z^5 + 105z^3 - 105z. $$Numerical simulations
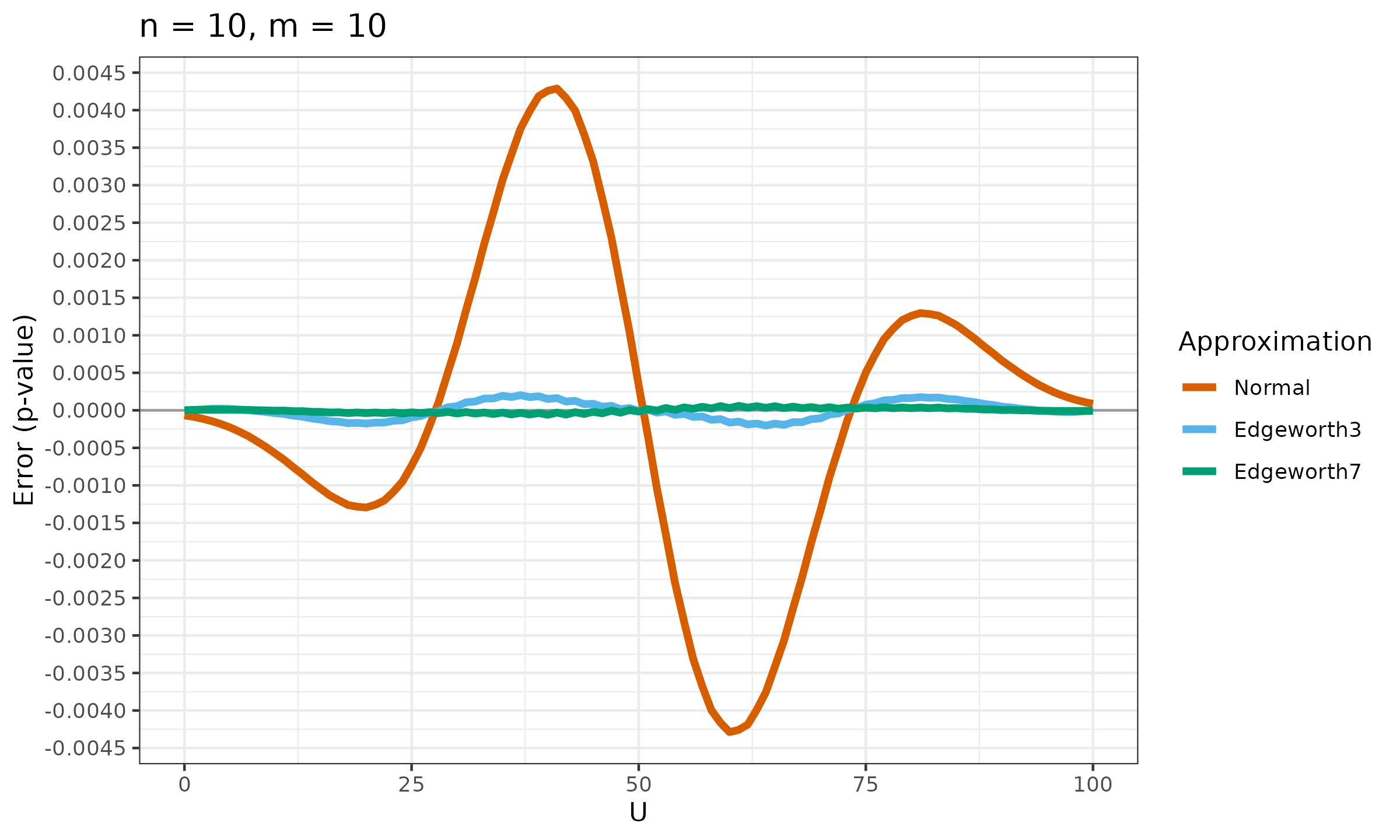
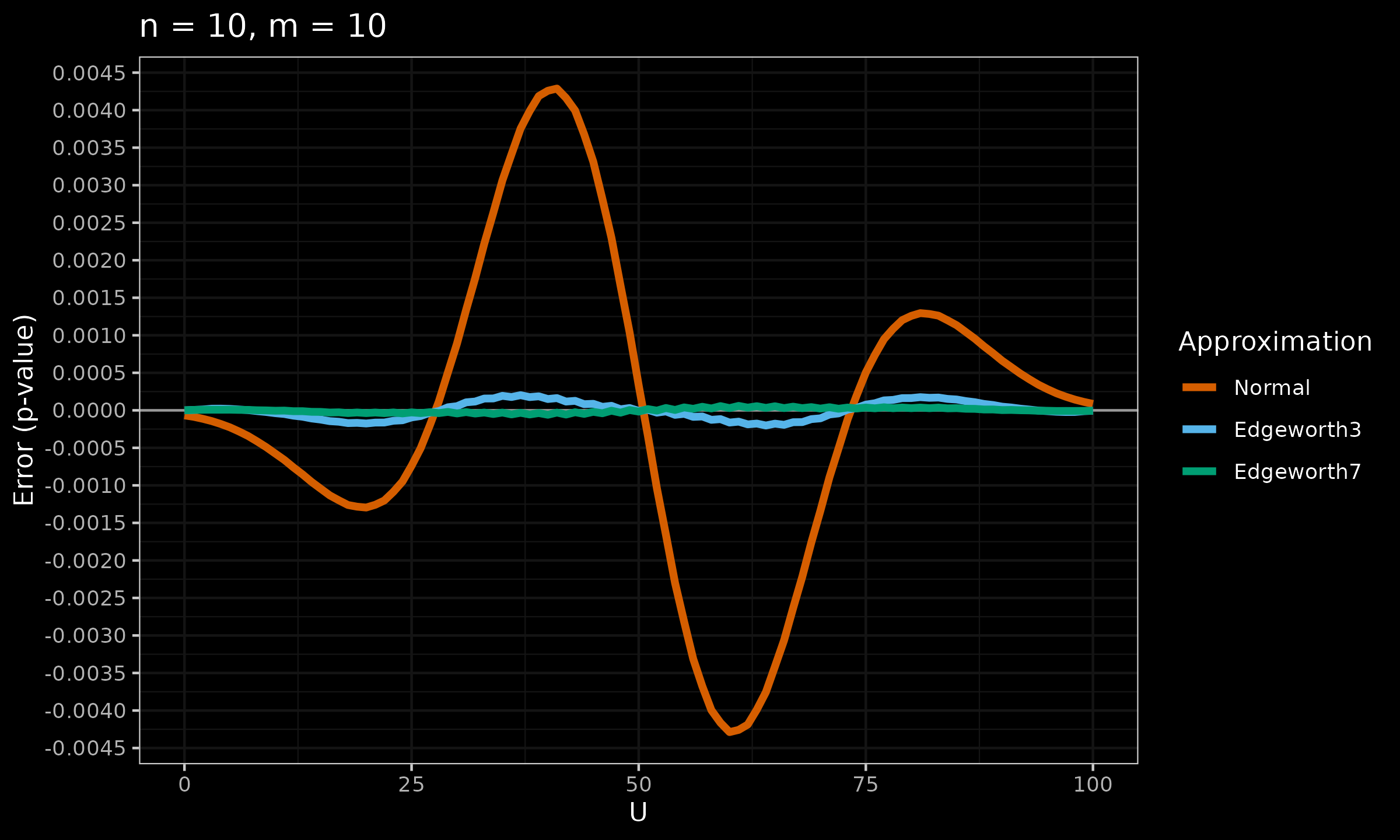
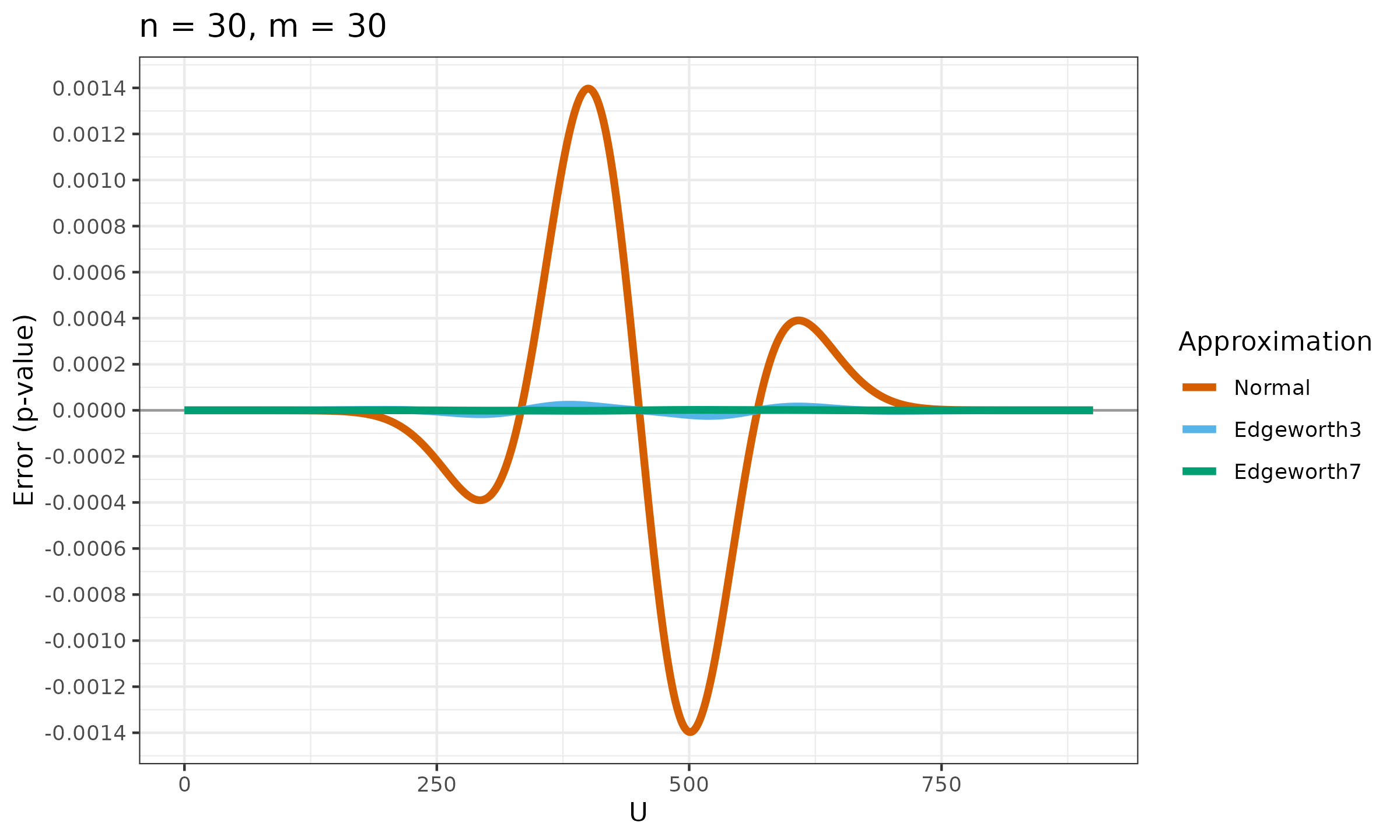
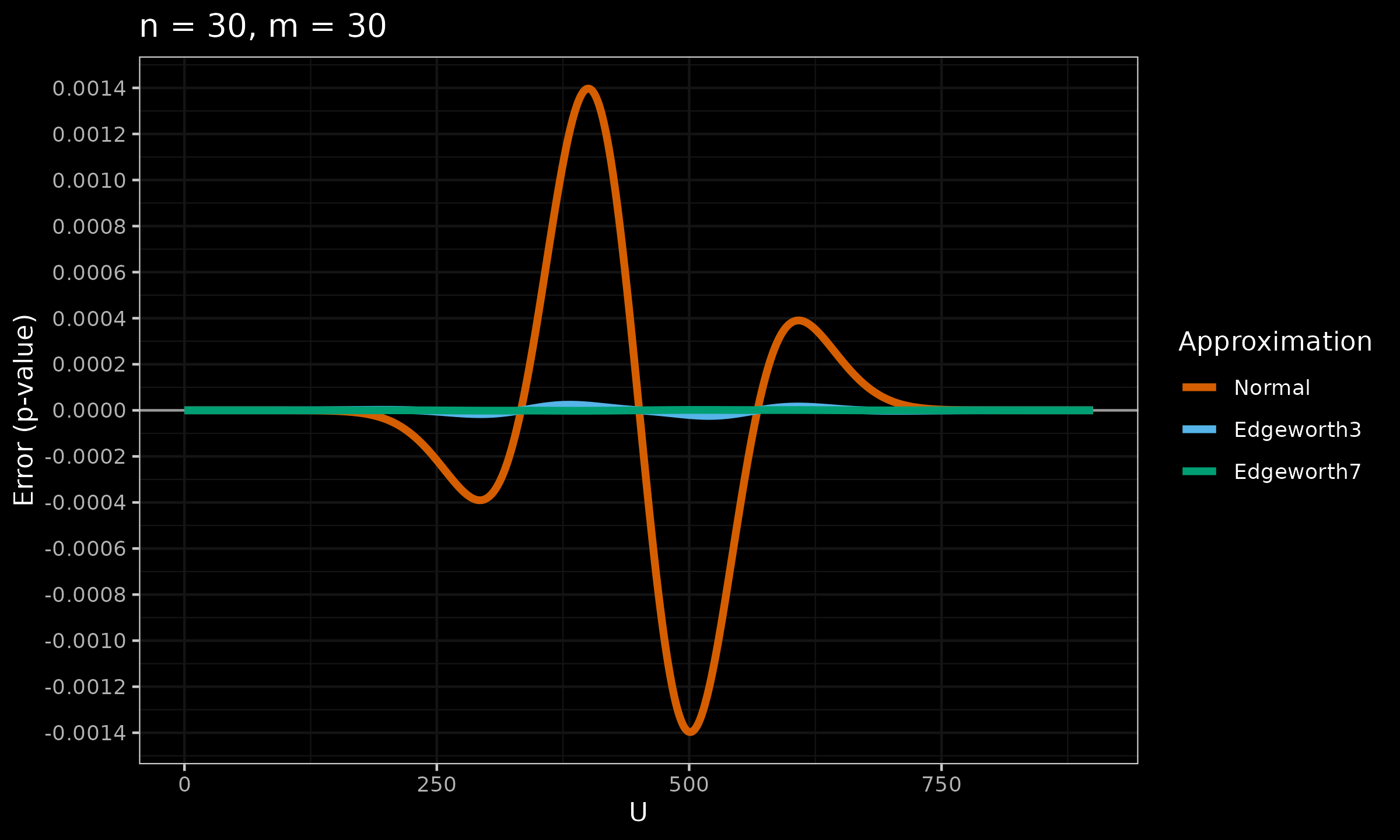
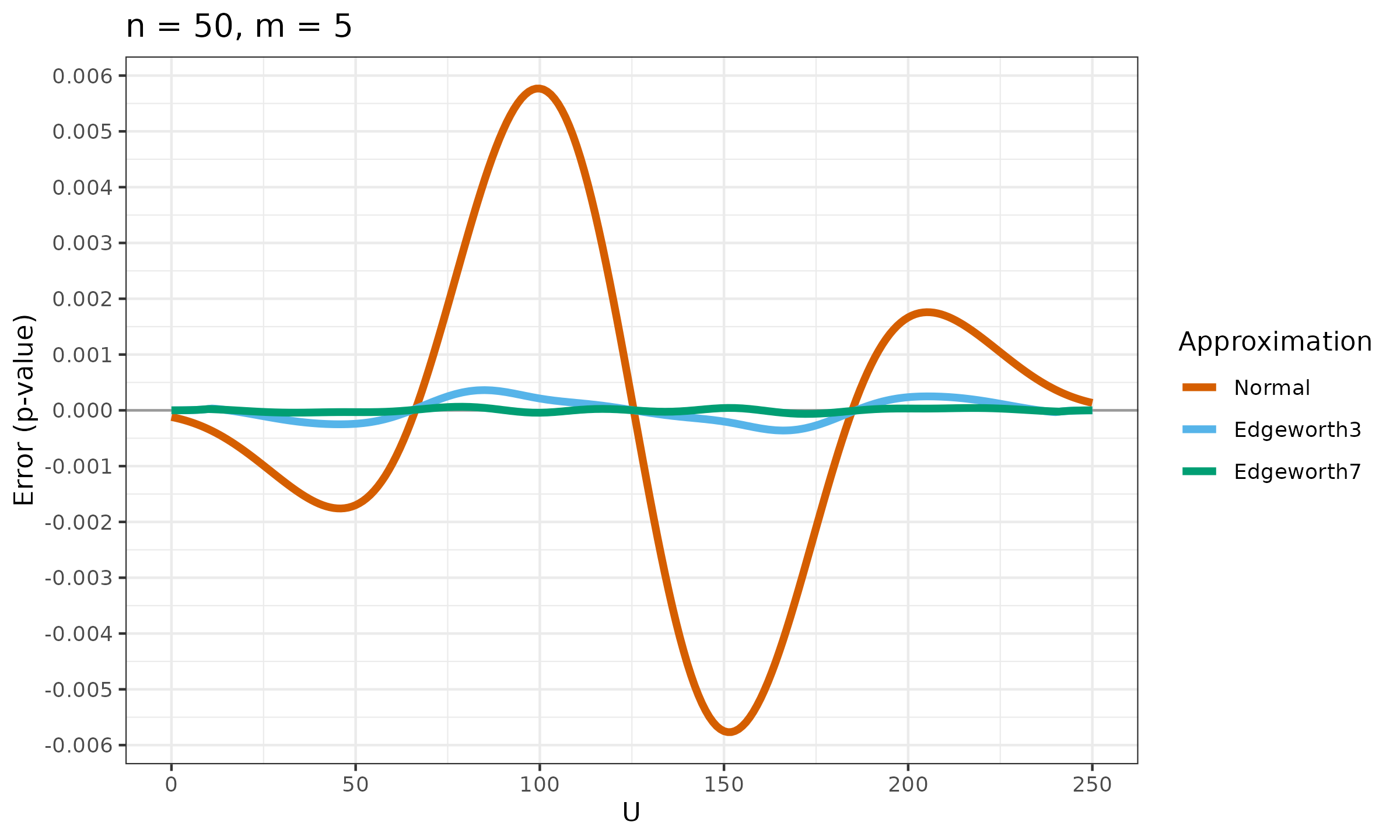
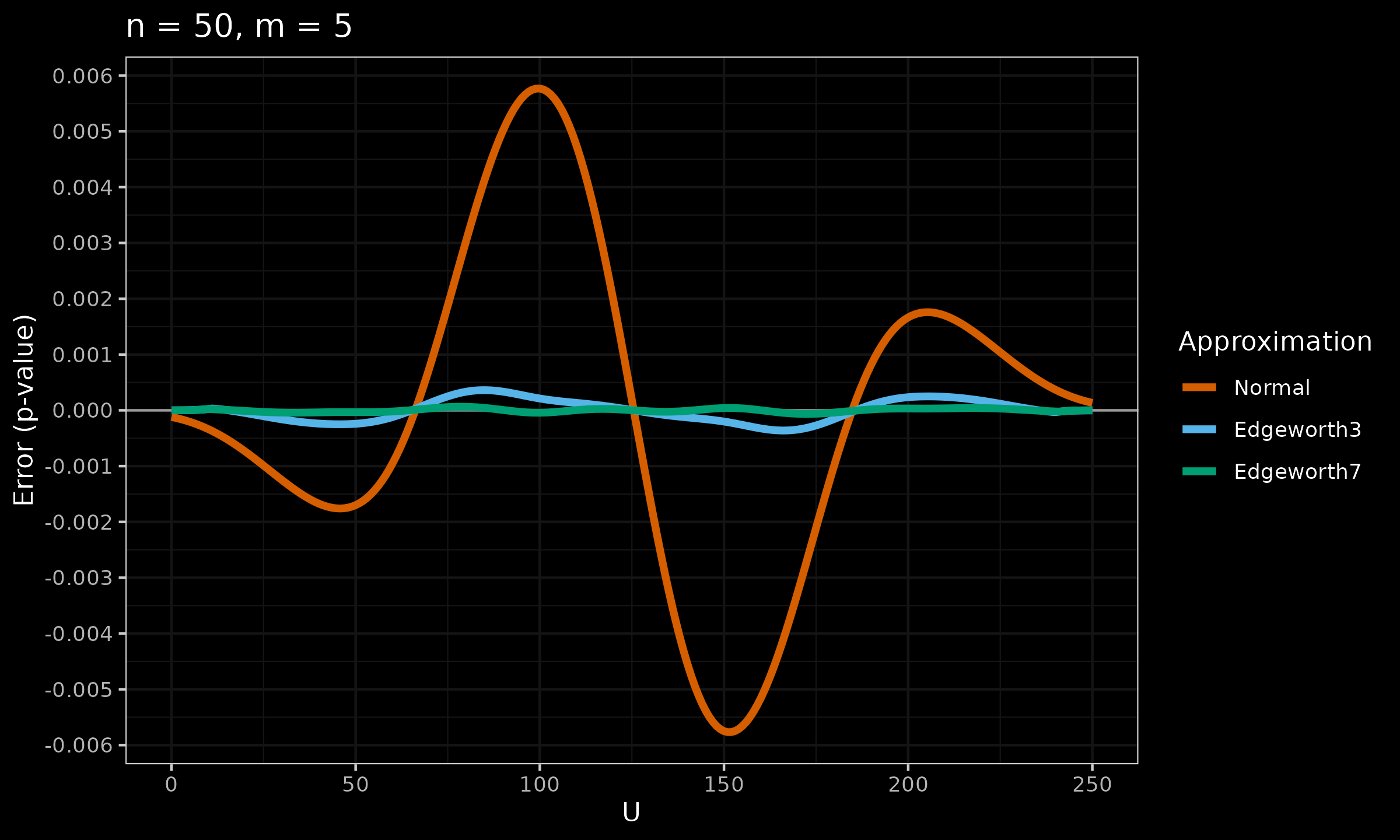
Now let’s explore the accuracy of $p_{E3}$ and $p_{E7}$ against the normal approximation:
As we can see, $p_{E7}$ looks much better than $p_{E3}$ (especially in the middle part).
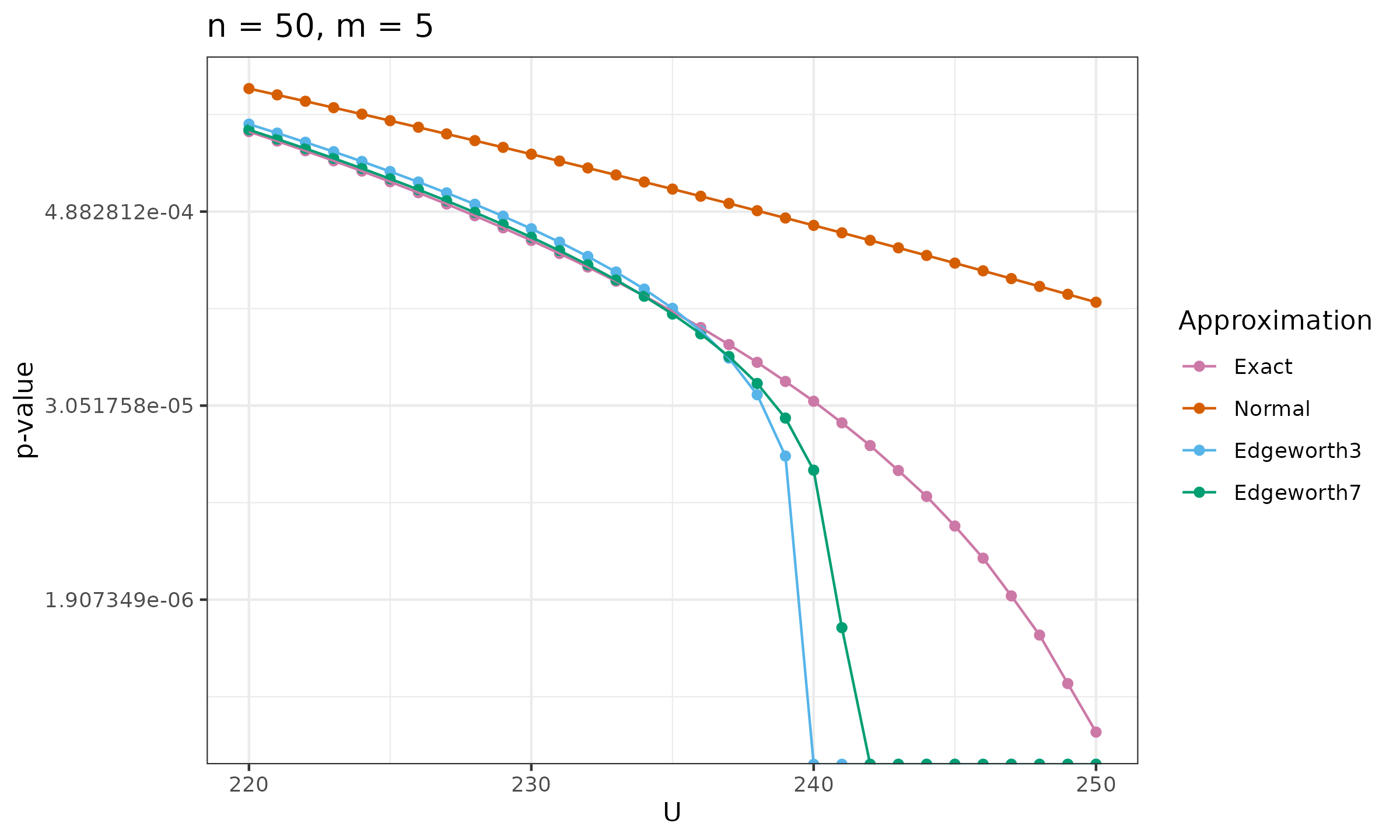
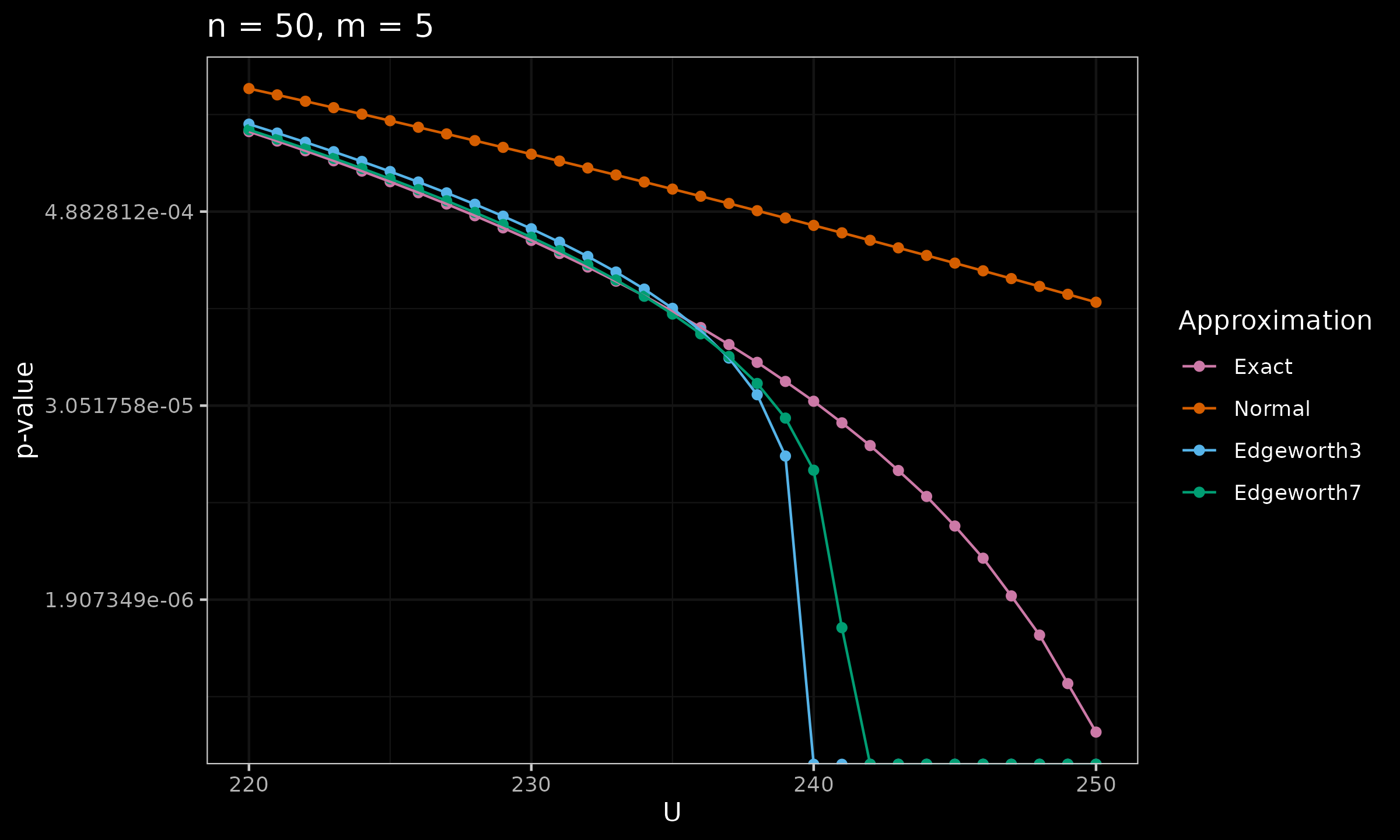
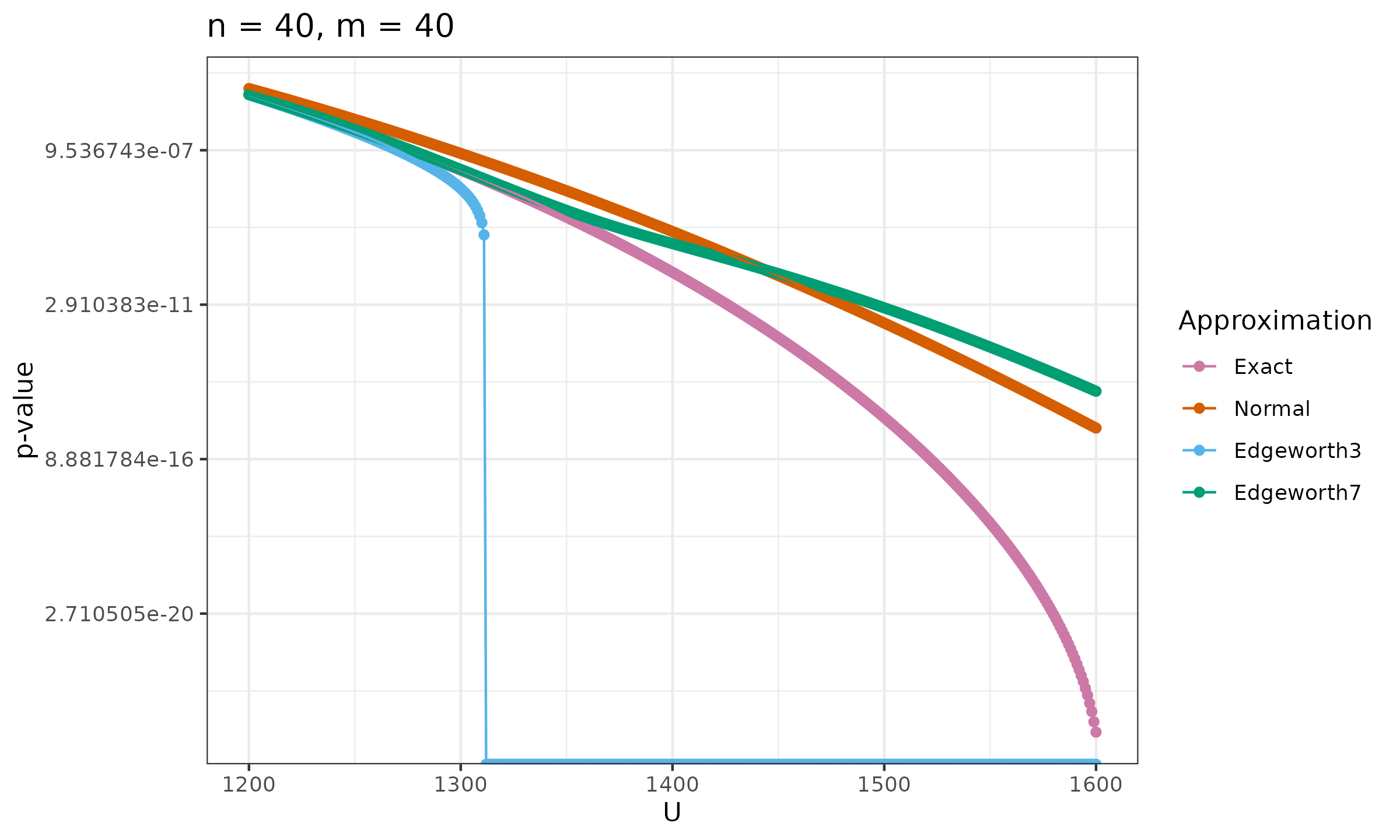
Now let’s look at the original p-values in some additional cases (logarithmic scale is used):
As we can see, $p_{E7}$ has a broader range of values, for which it produces more accurate results. However, it can behave worse than the normal distribution at the distribution tails.
References
- [Bean2004]
Raphaël Bean, Sorana Froda, and Constance Van Eeden. “The Normal, Edgeworth, Saddlepoint and Uniform Approximations to the Wilcoxon–Mann–Whitney Null-Distribution: A Numerical Comparison.” Journal of Nonparametric Statistics 16, no. 1–2 (February 2004): 279–88.
DOI: 10.1080/10485250310001622677 - [Fix1955]
Fix, Evelyn, and J. L. Hodges Jr. “Significance probabilities of the Wilcoxon test.” The Annals of Mathematical Statistics (1955): 301-312.
DOI:10.1214/aoms/1177728547 - [Mann1947]
Mann, H., and D. Whitney. “Controlling the false discovery rate: A practical and powerful approach to multiple testing.” Ann. Math. Stat 18, no. 1 (1947): 50-60.
DOI:10.1214/aoms/1177730491 - [Hodges1990]
Hodges Jr, J. L., Philip H. Ramsey, and Sergio Wechsler. “Improved significance probabilities of the Wilcoxon test.” Journal of Educational Statistics 15, no. 3 (1990): 249-265.
DOI:10.3102/10769986015003249 - [Ury1997]
Ury, Hans K. “A comparison of some approximations to the Wilcoxon-Mann-Whitney distribution.” Communications in Statistics-Simulation and Computation 6, no. 2 (1977): 181-197.
DOI:10.1080/03610917708812038 - [Zhong2021]
Zhong, Dewei, and John Kolassa. “Moments and Cumulants of the Bivariate Mann-Whitney Statistic for Two-Stage Trials.” Biomedical Journal of Scientific & Technical Research 35, no. 1 (2021): 27353-27358.
DOI:10.26717/BJSTR.2021.35.005654 - [Wiel1998]
van de Wiel, M. A. Edgeworth expansions with exact cumulants for two-sample linear rank statistics. TU, 1998.
https://pure.tue.nl/ws/files/1580743/513894.pdf - [Harremoes2005]
Harremoës, Peter. “Maximum entropy and the Edgeworth expansion.” In IEEE Information Theory Workshop, 2005., pp. 4-pp. IEEE, 2005.
DOI:10.1109/ITW.2005.1531858 - [Hall2013]
Hall, Peter. The bootstrap and Edgeworth expansion. Springer Science & Business Media, 2013.
DOI:10.1007/978-1-4612-4384-7 - [Hwang2019]
Hwang, Jungbin. “Note on Edgeworth Expansions and Asymptotic Refinements of Percentile t-Bootstrap Methods.” (2019).
https://hwang.econ.uconn.edu/wp-content/uploads/sites/1837/2020/08/Edgeworth_Expansion_Dec_05_2019_b.pdf - [Porter1972]
Ralph Edwin Porter Jr (1972) “Normal and Edgeworth approximations to the distribution of the Wilcoxon-Mann-Whitney statistic”
https://shareok.org/bitstream/handle/11244/24151/Thesis-1974-P847n.pdf