Mann-Whitney U test and heteroscedasticity

Mann-Whitney U test is a good nonparametric test, which mostly targets changes in locations. However, it doesn’t properly support all types of differences between the two distributions. Specifically, it poorly handles changes in variance. In this post, I briefly discuss its behavior in reaction to scaling a distribution without introducing location changes.

Let us consider two random variables $X$ and $Y$ from two different distributions. $X$ follows the standard normal distribution, $Y$ follows a normal distribution with customizable variance:

$$ X \sim \mathcal{N}(0, 1); \quad Y \sim \mathcal{N}(0, \sigma^2). $$

Now let us recall the hypothesis of the classic Mann-Whitney U test:

• $H_0$: the distributions are identical;
• $H_1$: one distribution is stochastically larger/smaller than another.

In our case, both hypotheses are wrong. Indeed, if $\sigma \neq 1$, the distributions are not identical. Meanwhile, they are stochastically equal for any value of $\sigma$:

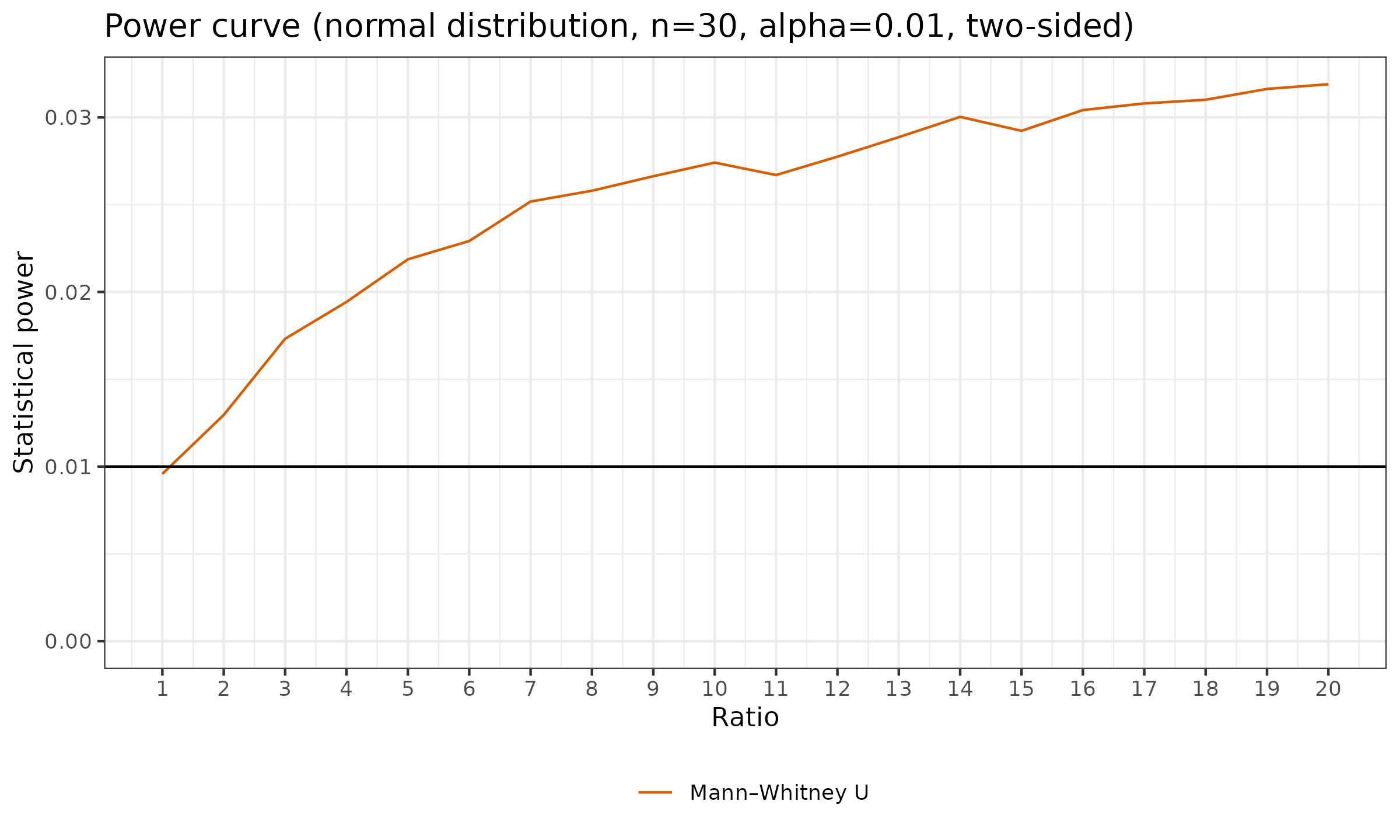
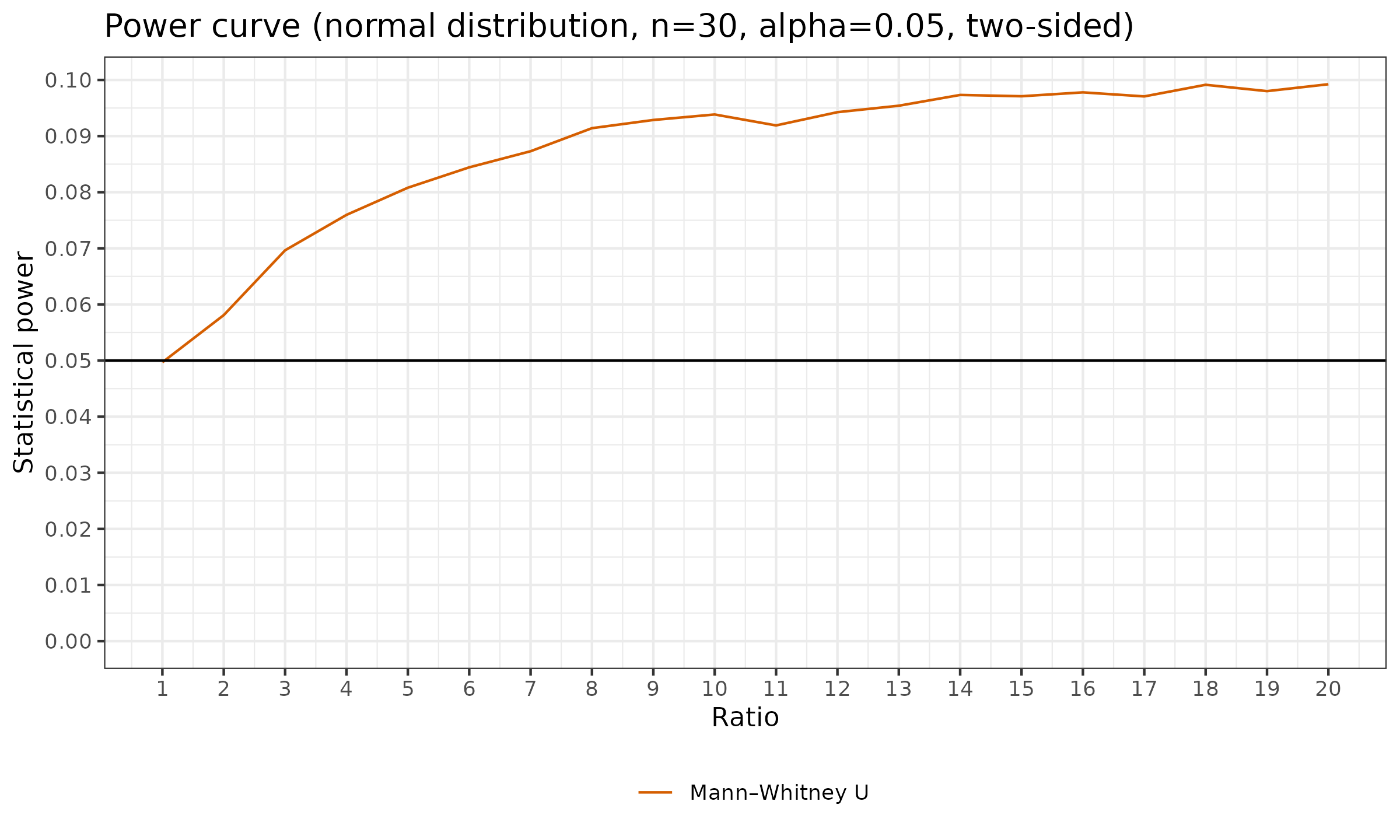
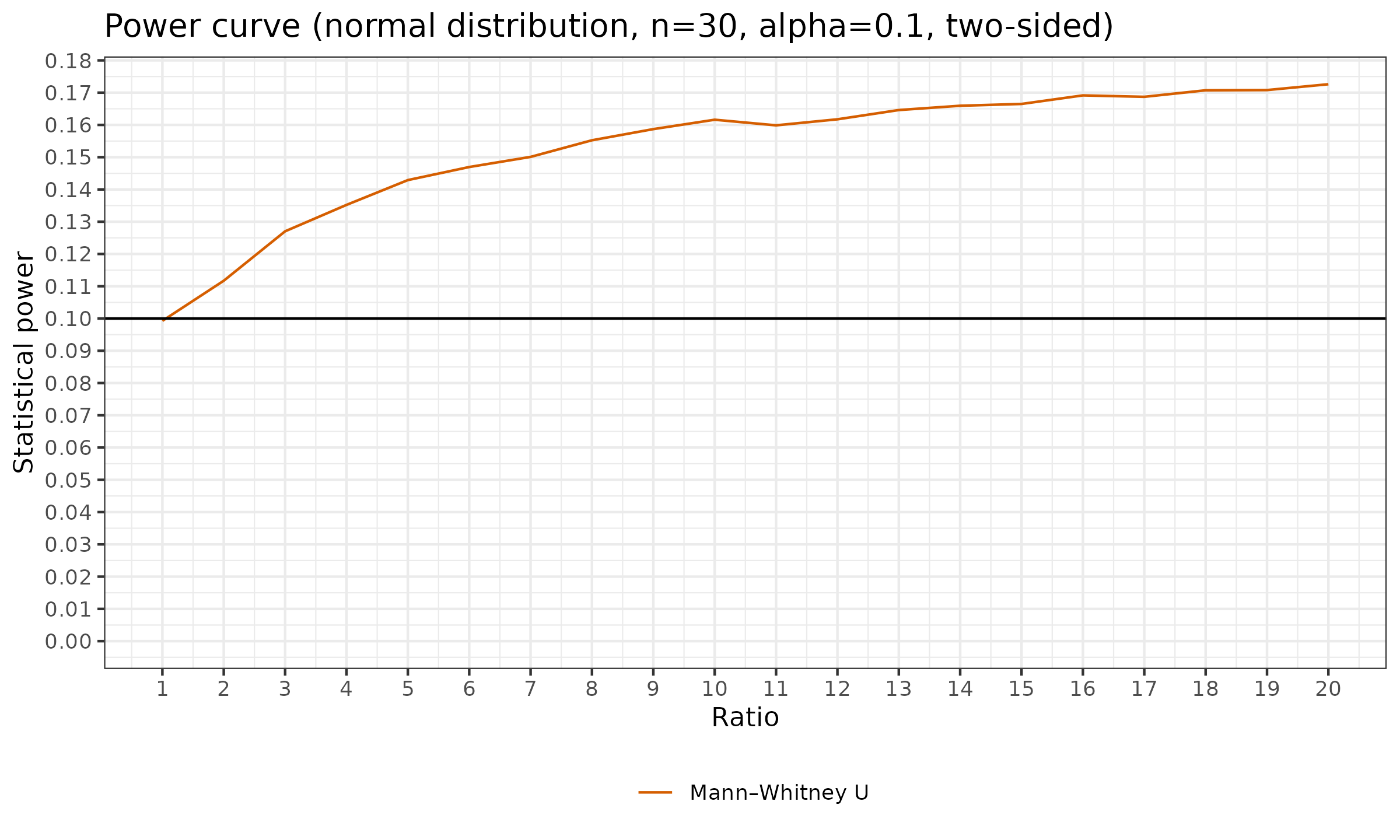
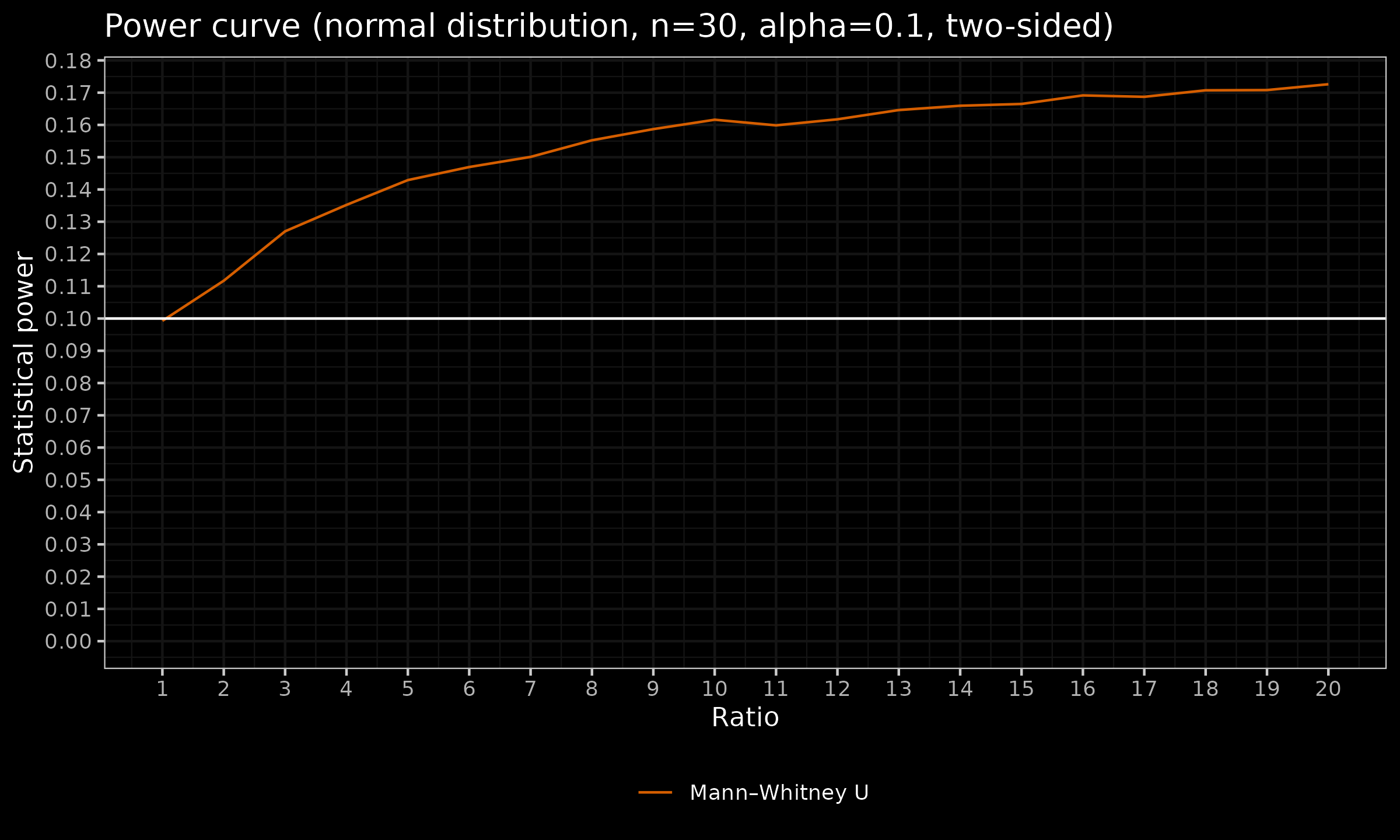
$$ \forall \sigma: \quad \mathbb{P}(X < Y) = \mathbb{P}(X > Y) = 0.5. $$

Let us explore the power curves of the two-sided Mann-Whitney U test, $n=30$, $\alpha \in \{ 0.01, 0.05, 0.10 \}$:

These are quite interesting pictures: while $H_1$ is false and the distributions are stochastically equal, the Mann-Whitney U test is sensitive to changes in $\sigma$. While we increase $\sigma$ (the X axis), we observe a small increase in statistical power. However, it seems that the power values are bounded, and they do not converge to $1$ while we increase $\sigma$ or the sample size $n$. With reasonable values of the statistical significance level $\alpha$, it is impossible to achieve reasonable values of the statistical power. Therefore, the Mann-Whitney U test is not suitable to detect changes in the variance. A better option for such a situation is the Ansari-Bradley test.