Optimal quantile absolute deviation

We consider the quantile absolute deviation around the median defined as follows:

$$ \newcommand{\E}{\mathbb{E}} \newcommand{\PR}{\mathbb{P}} \newcommand{\Q}{\operatorname{Q}} \newcommand{\OQAD}{\operatorname{OQAD}} \newcommand{\QAD}{\operatorname{QAD}} \newcommand{\median}{\operatorname{median}} \newcommand{\Exp}{\operatorname{Exp}} \newcommand{\SD}{\operatorname{SD}} \newcommand{\V}{\mathbb{V}} \QAD(X, p) = K_p \Q(|X - \median(X)|, p), $$

where $\Q$ is a quantile estimator, and $K_p$ is a scale constant which we use to make $\QAD(X, p)$ an asymptotically consistent estimator for the standard deviation under the normal distribution.

In this post, we get the exact values of the $K_p$ values, derive the corresponding equation for the asymptotic Gaussian efficiency of $\QAD(X, p)$, and find the point in which $\QAD(X, p)$ achieves the highest Gaussian efficiency.

Asymptotic consistency constants for QAD

Let us assume that $X$ follows the standard normal distribution $\mathcal{N}(0, 1)$. Since we want to achieve $\lim_{n \to \infty} \E[\QAD(X, p)] = 1$, we have

$$ \lim_{n \to \infty} \E[\QAD(X, p)] = \frac{1}{K_p}. $$

Using the exact equation for the $\QAD(X, p)$ of the normal distribution, we get the exact value for the asymptotic consisency constant value:

$$ K_p = \dfrac{1}{\Phi^{-1}((p+1)/2)}. $$

Asymptotic Gaussian efficiency of QAD

In this section, we consider the asymptotic relative statistical efficiency of the $\QAD$ against the standard deviation under the normal distribution (Gaussian efficiency).

We have already derived the equation for the Gaussian efficiency in the non-scaled case. Using the value of $K_p$, it is easy to update the obtained equation for the scaled case:

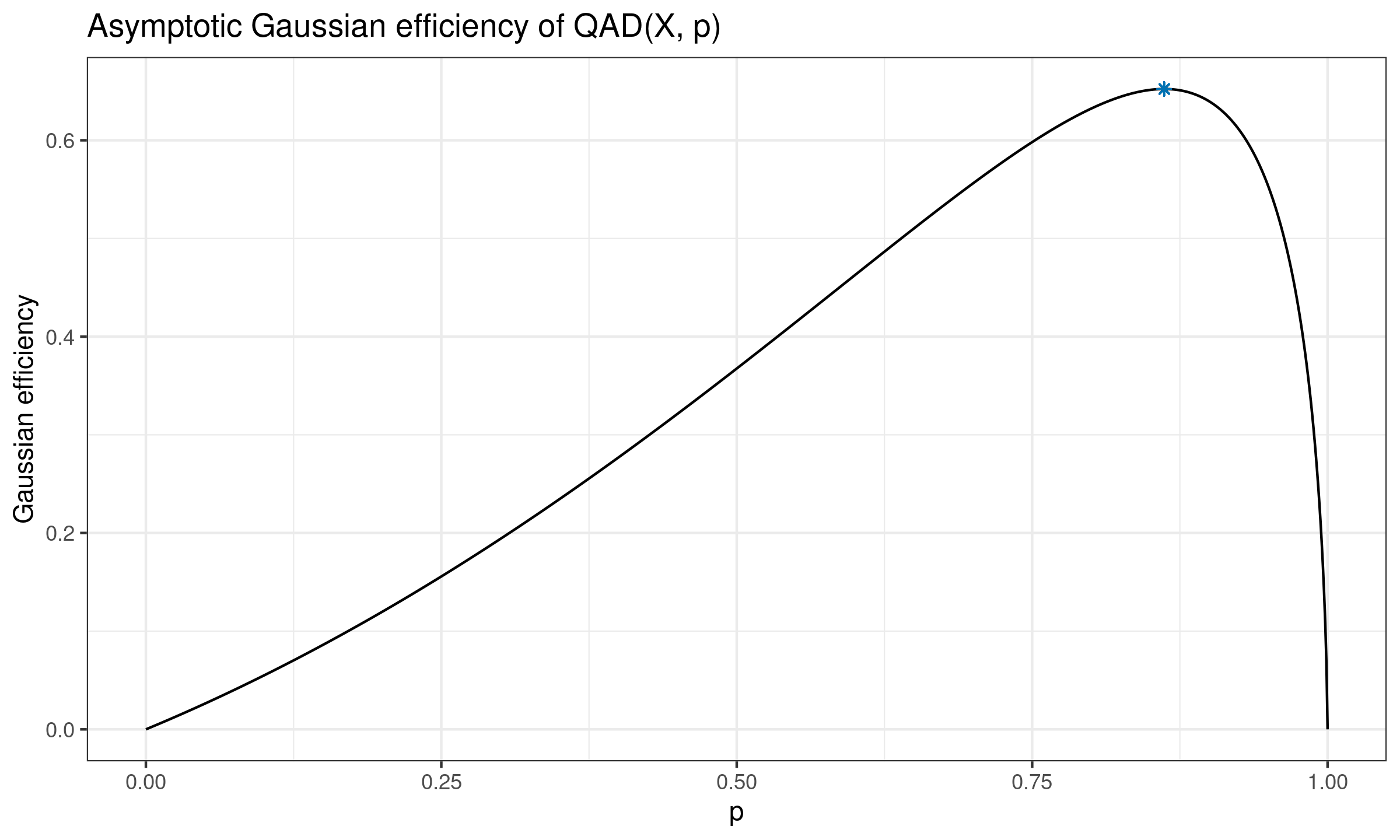
$$ \begin{split} \lim_{n \to \infty} e(\QAD_n(X, p),\; \SD_n(X)) = \lim_{n \to \infty} \frac{\V[\SD_n(X)]}{\V[\QAD_n(X, p)]} = \\ = \Bigg( \frac{1}{\big(\Phi^{-1}((p+1)/2)\big)^2} \pi p(1-p) \exp\Big(\big(\Phi^{-1}((p+1)/2)\big)^2 \Big) \Bigg)^{-1} = \\ = \frac{\big(\Phi^{-1}((p+1)/2)\big)^2}{\pi p(1-p) \exp\Big(\big(\Phi^{-1}((p+1)/2)\big)^2 \Big)}. \end{split} $$

Here is the corresponding plot:

We can see that the presented function is unimodal with a single maximum point. Let us denote the location of this point as $\rho_o$. This value can be obtained numerically:

$$ \rho_o \approx 0.861678977787423 \approx 86.17\%. $$

Optimal quantile absolute deviation

We define the optimal quantile absolute deviation by $\OQAD(X) = QAD(X, \rho_o)$. It can be interested to consider this measure of dispersion since it gives the highest Gaussian efficiency across all $\QAD(X, p)$ estimators ($65.22\%$). The corresponding breakdown point is $1 - \rho_o \approx 13.83\%$.