Fast implementation of the moving quantile based on the partitioning heaps

by Andrey Akinshin · 2020-12-29

Imagine you have a time series. Let’s say, after each new observation, you want to know an “average” value across the last $L$ observations. Such a metric is known as a moving average (or rolling/running average).

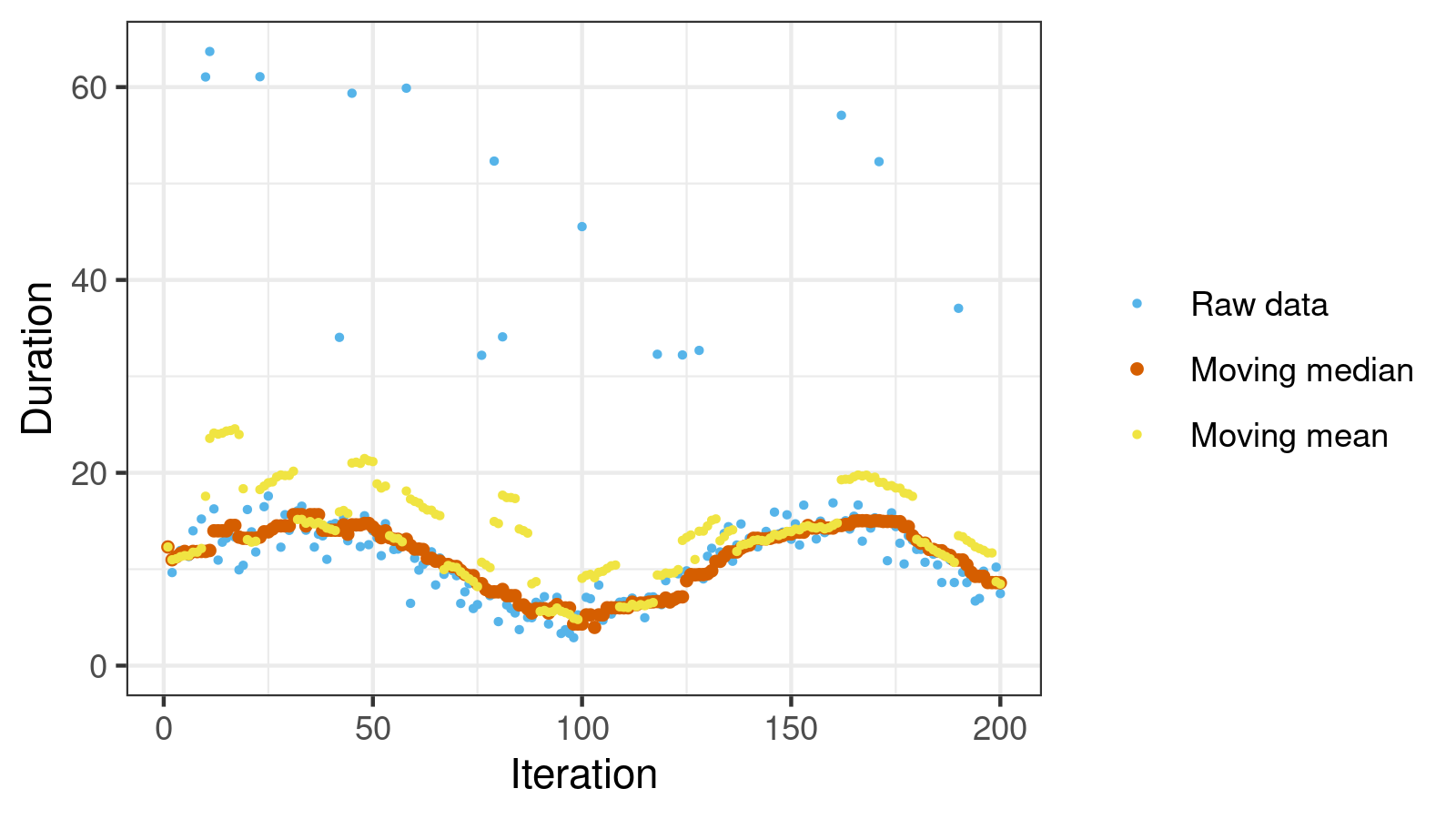
The most popular moving average example is the moving mean. It’s easy to efficiently implement this metric. However, it has a major drawback: it’s not robust. Outliers can easily spoil the moving mean and transform it into a meaningless and untrustable metric.

Fortunately, we have a good alternative: the moving median. Typically, it generates a stable and smooth series of values. In the below figure, you can see the difference between the moving mean and the moving median on noisy data.

The moving median also has a drawback: it’s not easy to efficiently implement it. Today we going to discuss the Hardle-Steiger method to estimate the median (memory: $O(L)$, element processing complexity: $O(log(L))$, median estimating complexity: $O(1)$). Also, we will learn how to calculate the moving quantiles based on this method.

In this post, you will find the following:

  • An overview of the Hardle-Steiger method
  • A simple way to implement the Hardle-Steiger method
  • Moving quantiles inspired by the Hardle-Steiger method
  • How to process initial elements
  • Reference C# implementation

An overview of the Hardle-Steiger method

This method is described in [Hardle1995]. The core idea is based on a data structure that contains two joined heaps:


In this figure, you see an example for $L=21$. It contains:

  • $H_1 .. H_{10}$: min heap
  • $H_{-1} .. H_{-10}$: max heap
  • $H_0$: a node that joins two heaps

The $H$ array contain the last $L$ elements of the time series and satisfy the following conditions:

  • $\max(H_{-2i},\; H_{-2i-1}) \leq H_{-i} \leq H_0$
  • $\min(H_{2i},\; H_{2i+1}) \geq H_{i} \geq H_0$

Thus, $H_0$ is less than all elements in the upper heap (positive indexes) and greater than all elements in the lower heap (negative indexes). Since we have an equal number of elements in both heaps, $H_0$ represents the median value.

That’s all! If we want to know the current value of the moving median, we should just take the value of $H_0$. The suggested algorithm has the following characteristics:

  • Amount of memory: $O(L)$
  • Element processing complexity: $O(log(L))$
  • Median estimating complexity: $O(1)$

Now we should learn how to invalidate this data structure for new observations.

A simple way to implement the Hardle-Steiger method

The most famous implementation of the Hardle-Steiger method is the Turlach implementation in C. It’s used in the R’s function runmed. This implementation doesn’t look simple, so it’s not easy to replicate it using another language (you can find a few StackOverflow discussion about this implementation here and here). So, I looked at the above picture and came up with my own way to implement this algorithm (you can find a reference C# implementation at the end of this post). It differs from the Turlach implementation and from the suggested approach in the original paper, but it still uses the same idea.

We are going to keep three array with numbers:

  • double[] h: the elements of the partitioning heaps
  • int[] heapToElementIndex: returns the original element index for the given heap element
  • int[] elementToHeapIndex: returns the heap index for the given element index

The swap routine is trivial:

private void Swap(int heapIndex1, int heapIndex2)
{
    int elementIndex1 = heapToElementIndex[heapIndex1];
    int elementIndex2 = heapToElementIndex[heapIndex2];
    double value1 = h[heapIndex1];
    double value2 = h[heapIndex2];

    h[heapIndex1] = value2;
    h[heapIndex2] = value1;
    heapToElementIndex[heapIndex1] = elementIndex2;
    heapToElementIndex[heapIndex2] = elementIndex1;
    elementToHeapIndex[elementIndex1] = heapIndex2;
    elementToHeapIndex[elementIndex2] = heapIndex1;
}

To simplify the calculations, we take all the element indexes by modulo $L$. Since we have exactly $L$ subsequent indexes at each moment, there are no index collisions.

When we get a new element x[i], we should replace the h[i % L] value by x[i]. Next, we should do a series of swaps to repair the heap conditions. In the classic heap implementation, we usually have two Sift methods: SiftUp and SiftDown. To reduce the number of cases, we are going to implement a generic Sift routine according to the following scheme:

  • Consider the current heap node and lower neighbor nodes. If we have any lower neighbor nodes that are larger than the current node, we swap the current node with the node that has the maximum value (across considered nodes).
  • Otherwise, we consider the current heap node and the upper neighbor nodes. Repeat the previous step with an opposite sign.
  • If we swapped the current node with a lower or upper neighbor node, we repeat two previous steps with the new node location. Otherwise, we stop.

This logic still have a lot of cases that should be handled, but it’s not so hard to implement it. See the reference implementation at the end of this post for details.

Moving quantiles inspired by the Hardle-Steiger method

The original algorithm was designed only for the moving median. Let’s generalize it to calculate any moving quantile.

We can express the Hardle-Steiger method in terms of order statistics. For the given odd $L$, we can define $k = (L-1)/2$. The median element across the last $L$ numbers is the $(k+1)^\textrm{th}$ smallest element (assuming one-base indexing). $H_0$ is the request number because it’s larger than all of the elements in the lower heap (which contains exactly $k$ elements) and smaller than all of the elements in the upper heap (which also contains $k$ elements).

Now let’s change the heap sizes! For any $k \in [0; L-1]$, we can consider the lower heap of size $k$ and the upper heap of size $L-k-1$. In this case, $H_0$ will represent the $(k+1)^\textrm{th}$ smallest element. The $p^\textrm{th}$ quantile ($p \in [0; 1]$) can be estimated as the $\lfloor p(L-1) \rfloor^\textrm{th}$ smallest element! Note that now the window size can be an arbitrary positive number (unlike the original approach which supports only odd $L$ values).

It looks simple, so I was surprised that I didn’t manage to find this idea anywhere. If you find any references where this approach is explained, please let me know.

How to process initial elements

Let’s say that the windows size $L=21$, we estimate the median $k=10$, but we are at the beginning of our time series, and we have only 13 elements. What should we return? There two possible strategies here:

  • Order Statistics
    Since the $k^\textrm{th}$ smallest element was requested, we should return it. In the above example, it would be the $10^\textrm{th}$ smallest element from the 13 observed numbers.
  • Quantile Approximation
    Since the median was requested, we should return it. In the above example, it would be $7^\textrm{th}$ smallest element from the 13 observed numbers.

Also, there are other strategies (e.g., repeating the first element). However, in my opinion, other approaches don’t satisfy the principle of least astonishment, so we are not going to discuss them.

The two presented strategy define the way of the heap initialization (how we process $x[i]$ for $i < L$). We start with two empty heaps. Once we got the first element, we always put it into $H_0$. Next, we should add subsequent elements to the lower or upper heap depending on the chosen strategy:

  • Order Statistics
    We add elements to the lower heap until it’s full. After that, we add elements to the upper heap.
  • Quantile Approximation
    We choose the lower or upper heap trying to keep the ratio $\textrm{LowerHeapSize} / (\textrm{LowerHeapSize} + \textrm{UpperHeapSize})$ close to the target quantile.

Reference C# implementation

Below you can find a full C# implementation of the moving quantile according to the above approach. You can also use it with the latest nightly version (0.3.0-nightly.86+) of Perfolizer (you need PartitioningHeapsMovingQuantileEstimator).

/// <summary>
/// A moving selector based on a partitioning heaps.
/// Memory: O(windowSize).
/// Add complexity: O(log(windowSize)).
/// GetValue complexity: O(1).
/// 
/// <remarks>
/// Based on the following paper:
/// Hardle, W., and William Steiger. "Algorithm AS 296: Optimal median smoothing." Journal of the Royal Statistical Society.
/// Series C (Applied Statistics) 44, no. 2 (1995): 258-264.
/// </remarks>
/// </summary>
public class PartitioningHeapsMovingQuantileEstimator
{
    private readonly int windowSize, k;
    private readonly double[] h;
    private readonly int[] heapToElementIndex;
    private readonly int[] elementToHeapIndex;
    private readonly int rootHeapIndex, lowerHeapMaxSize;
    private readonly MovingQuantileEstimatorInitStrategy initStrategy;
    private int upperHeapSize, lowerHeapSize, totalElementCount;

    public PartitioningHeapsMovingQuantileEstimator(int windowSize, int k,
        MovingQuantileEstimatorInitStrategy initStrategy = MovingQuantileEstimatorInitStrategy.QuantileApproximation)
    {
        this.windowSize = windowSize;
        this.k = k;
        h = new double[windowSize];
        heapToElementIndex = new int[windowSize];
        elementToHeapIndex = new int[windowSize];

        lowerHeapMaxSize = k;
        this.initStrategy = initStrategy;
        rootHeapIndex = k;
    }

    private void Swap(int heapIndex1, int heapIndex2)
    {
        int elementIndex1 = heapToElementIndex[heapIndex1];
        int elementIndex2 = heapToElementIndex[heapIndex2];
        double value1 = h[heapIndex1];
        double value2 = h[heapIndex2];

        h[heapIndex1] = value2;
        h[heapIndex2] = value1;
        heapToElementIndex[heapIndex1] = elementIndex2;
        heapToElementIndex[heapIndex2] = elementIndex1;
        elementToHeapIndex[elementIndex1] = heapIndex2;
        elementToHeapIndex[elementIndex2] = heapIndex1;
    }

    private void Sift(int heapIndex)
    {
        int SwapWithChildren(int heapCurrentIndex, int heapChildIndex1, int heapChildIndex2, bool isUpperHeap)
        {
            bool hasChild1 = rootHeapIndex - lowerHeapSize <= heapChildIndex1 && heapChildIndex1 <= rootHeapIndex + upperHeapSize;
            bool hasChild2 = rootHeapIndex - lowerHeapSize <= heapChildIndex2 && heapChildIndex2 <= rootHeapIndex + upperHeapSize;

            if (!hasChild1 && !hasChild2)
                return heapCurrentIndex;

            if (hasChild1 && !hasChild2)
            {
                if (h[heapIndex] < h[heapChildIndex1] && !isUpperHeap || h[heapIndex] > h[heapChildIndex1] && isUpperHeap)
                {
                    Swap(heapIndex, heapChildIndex1);
                    return heapChildIndex1;
                }
                return heapCurrentIndex;
            }

            if (hasChild1 && hasChild2)
            {
                if ((h[heapIndex] < h[heapChildIndex1] || h[heapIndex] < h[heapChildIndex2]) && !isUpperHeap ||
                    (h[heapIndex] > h[heapChildIndex1] || h[heapIndex] > h[heapChildIndex2]) && isUpperHeap)
                {
                    int heapChildIndex0 =
                        h[heapChildIndex1] > h[heapChildIndex2] && !isUpperHeap ||
                        h[heapChildIndex1] < h[heapChildIndex2] && isUpperHeap
                            ? heapChildIndex1
                            : heapChildIndex2;
                    Swap(heapIndex, heapChildIndex0);
                    return heapChildIndex0;
                }
                return heapCurrentIndex;
            }

            throw new InvalidOperationException();
        }

        while (true)
        {
            if (heapIndex != rootHeapIndex)
            {
                bool isUpHeap = heapIndex > rootHeapIndex;
                int heapParentIndex = rootHeapIndex + (heapIndex - rootHeapIndex) / 2;
                if (h[heapParentIndex] < h[heapIndex] && !isUpHeap || h[heapParentIndex] > h[heapIndex] && isUpHeap)
                {
                    Swap(heapIndex, heapParentIndex);
                    heapIndex = heapParentIndex;
                    continue;
                }
                else
                {
                    int heapChildIndex1 = rootHeapIndex + (heapIndex - rootHeapIndex) * 2;
                    int heapChildIndex2 = rootHeapIndex + (heapIndex - rootHeapIndex) * 2 + Math.Sign(heapIndex - rootHeapIndex);
                    int newHeapIndex = SwapWithChildren(heapIndex, heapChildIndex1, heapChildIndex2, isUpHeap);
                    if (newHeapIndex != heapIndex)
                    {
                        heapIndex = newHeapIndex;
                        continue;
                    }
                }
            }
            else // heapIndex == rootHeapIndex
            {
                if (lowerHeapSize > 0)
                {
                    int newHeapIndex = SwapWithChildren(heapIndex, heapIndex - 1, -1, false);
                    if (newHeapIndex != heapIndex)
                    {
                        heapIndex = newHeapIndex;
                        continue;
                    }
                }

                if (upperHeapSize > 0)
                {
                    int newHeapIndex = SwapWithChildren(heapIndex, heapIndex + 1, -1, true);
                    if (newHeapIndex != heapIndex)
                    {
                        heapIndex = newHeapIndex;
                        continue;
                    }
                }
            }

            break;
        }
    }

    public void Add(double value)
    {
        int elementIndex = totalElementCount % windowSize;

        int Insert(int heapIndex)
        {
            h[heapIndex] = value;
            heapToElementIndex[heapIndex] = elementIndex;
            elementToHeapIndex[elementIndex] = heapIndex;
            return heapIndex;
        }

        if (totalElementCount++ < windowSize) // Heap is not full
        {
            if (totalElementCount == 1) // First element
            {
                Insert(rootHeapIndex);
            }
            else
            {
                bool quantileApproximationCondition =
                    initStrategy == MovingQuantileEstimatorInitStrategy.QuantileApproximation &&
                    lowerHeapSize < k * totalElementCount / windowSize ||
                    initStrategy == MovingQuantileEstimatorInitStrategy.OrderStatistics;
                if (lowerHeapSize < lowerHeapMaxSize && quantileApproximationCondition)
                {
                    lowerHeapSize++;
                    int heapIndex = Insert(rootHeapIndex - lowerHeapSize);
                    Sift(heapIndex);
                }
                else
                {
                    upperHeapSize++;
                    int heapIndex = Insert(rootHeapIndex + upperHeapSize);
                    Sift(heapIndex);
                }
            }
        }
        else
        {
            // Replace old element
            int heapIndex = elementToHeapIndex[elementIndex];
            Insert(heapIndex);
            Sift(heapIndex);
        }
    }

    public double GetQuantile()
    {
        if (totalElementCount == 0)
            throw new IndexOutOfRangeException("There are no any values");
        if (initStrategy == MovingQuantileEstimatorInitStrategy.OrderStatistics && k >= totalElementCount)
            throw new IndexOutOfRangeException($"Not enough values (n = {totalElementCount}, k = {k})");
        return h[rootHeapIndex];
    }
}

/// <summary>
/// Defines how a moving quantile estimator calculates the target quantile value
/// when the total number of elements is less than the window size
/// </summary>
public enum MovingQuantileEstimatorInitStrategy
{
    /// <summary>
    /// Approximate the target quantile.
    ///
    /// <example>
    /// windowSize = 5, k = 2 (the median)
    /// If the total number of elements equals 3, the median (k = 1) will be returned 
    /// </example> 
    /// </summary>
    QuantileApproximation,

    /// <summary>
    /// Return the requested order statistics
    ///
    /// <example>
    /// windowSize = 5, k = 2
    /// If the total number of elements equals 3, the largest element (k = 2) will be returned 
    /// </example> 
    /// </summary>
    OrderStatistics
}

Conclusion

In this post, we discussed the Hardle-Steiger method to estimate the moving median. Also, we built a generalization of this method to estimate any moving quantile. This approach is useful in monitoring when you want to get the average value of your time series using only recent elements. It’s optimal in terms of performance and memory footprint for medium-size windows. In future blog posts, I will show other approaches that estimate the moving quantile (that are optimal for small-size and big-size windows).

References