Performance exercise: Minimum
Performance is tricky. Especially, if you are working with very fast operations. In today benchmarking exercise, we will try to measure performance of two simple methods which calculate minimum of two numbers. Sounds easy? Ok, let’s do it, here are our guinea pigs for today:
int MinTernary(int x, int y) => x < y ? x : y;
int MinBitHacks(int x, int y) => x & ((x - y) >> 31) | y & (~(x - y) >> 31);
And here are some results:
| Random | Const | |||
|---|---|---|---|---|
| Ternary | BitHacks | Ternary | BitHacks | |
| LegacyJIT-x86 | ≈643µs | ≈227µs | ≈160µs | ≈226µs |
| LegacyJIT-x64 | ≈450µs | ≈123µs | ≈68µs | ≈123µs |
| RyuJIT-x64 | ≈594µs | ≈241µs | ≈180µs | ≈241µs |
| Mono-x64 | ≈203µs | ≈283µs | ≈204µs | ≈282µs |
What’s going on here? Let’s discuss it in detail.
Bit hacks
The first implementation looks obvious, but it has one significant problem: it could suffer from branch mispredictions because of a condition in the expression. Fortunately, it is possible to rewrite it without a branch with the help of bit hacks:
int MinBitHacks(int x, int y) => x & ((x - y) >> 31) | y & (~(x - y) >> 31);
Here we calculate (x-y), the sign of this expression depends on which number is less. Then, (x-y) >> 31 gives a bit mask which contains only zeros or ones. Next, we calculate an inverted mask: ~(x - y) >> 31. Now we and our operands and the corresponded bit masks (the minimum number get the 11...11 mask). That’s all: the or operator returns the correct result.
Here is an example for x=8 and y=3:
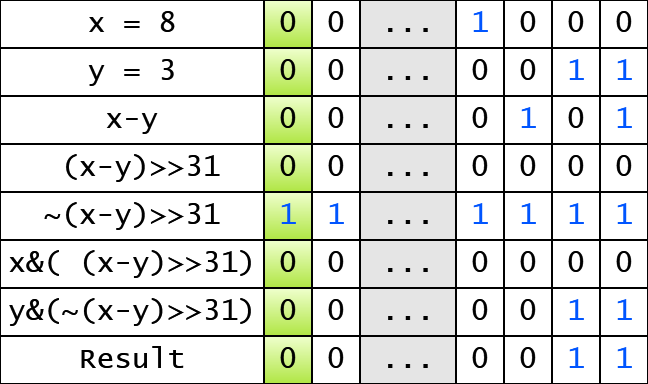
As you can see, here is no a branch here: we compute the minimum using only bit operations.
Performance spaces
It’s wrong to discuss the performance of some operations in general; we always should think about a space of the performance results (I call it performance space). Simplifying, you have to consider the following:
- Source code: there are different ways to write a benchmark which includes the
Minmethods. Today we will take twointarraysaandbwith some data and calculate the third arrayint[] cwherec[i] = Min(a[i], b[i])for eachi. - Data: we always should check different data patterns. In our case, we are analyzing the branch predictor, so it makes sense to check const and random input patterns.
- Environment: there are many different environments, today we will check only Full .NET Framework 4.6.2 (with 3 main JIT compilers:
LegacyJIT-x86,LegacyJIT-x64,RyuJIT-x64) and Mono 4.6.2 on Windows.
Benchmarks
Here the source code of my benchmarks (based on BenchmarkDotNet v0.10.1):
[LegacyJitX86Job, LegacyJitX64Job, RyuJitX64Job, MonoJob]
public class MinBench
{
const int N = 100001;
private int[] a, b, c;
public enum StrategyKind
{
Const, Random
}
[Params(StrategyKind.Const, StrategyKind.Random)]
public StrategyKind Strategy;
[Setup]
public void Setup()
{
a = new int[N];
b = new int[N];
c = new int[N];
var rnd = new Random(42);
for (int i = 0; i < N; i++)
{
switch (Strategy)
{
case StrategyKind.Const:
{
a[i] = 42;
b[i] = 42;
}
break;
case StrategyKind.Random:
{
a[i] = rnd.Next();
b[i] = rnd.Next();
}
break;
}
}
}
[Benchmark]
public void Ternary()
{
for (int i = 0; i < N; i++)
{
int x = a[i], y = b[i];
c[i] = x < y ? x : y;
}
}
[Benchmark]
public void BitHacks()
{
for (int i = 0; i < N; i++)
{
int x = a[i], y = b[i];
c[i] = x & ((x - y) >> 31) | y & (~(x - y) >> 31);
}
}
}
Raw results:
BenchmarkDotNet=v0.10.1, OS=Microsoft Windows NT 6.2.9200.0
Processor=Intel(R) Core(TM) i7-4702MQ CPU 2.20GHz, ProcessorCount=8
Frequency=2143475 Hz, Resolution=466.5321 ns, Timer=TSC
[Host] : Clr 4.0.30319.42000, 32bit LegacyJIT-v4.6.1586.0
LegacyJitX64 : Clr 4.0.30319.42000, 64bit LegacyJIT/clrjit-v4.6.1586.0;compatjit-v4.6.1586.0
LegacyJitX86 : Clr 4.0.30319.42000, 32bit LegacyJIT-v4.6.1586.0
Mono : Mono 4.6.2 (Visual Studio built mono), 64bit
RyuJitX64 : Clr 4.0.30319.42000, 64bit RyuJIT-v4.6.1586.0
| Method | Job | Strategy | Mean | StdDev |
|---|---|---|---|---|
| Ternary | LegacyJitX86 | Random | 643.9113 us | 2.8095 us |
| BitHacks | LegacyJitX86 | Random | 227.1344 us | 1.3270 us |
| Ternary | LegacyJitX86 | Const | 160.0779 us | 0.9276 us |
| BitHacks | LegacyJitX86 | Const | 225.7077 us | 0.7597 us |
| Ternary | LegacyJitX64 | Random | 450.7977 us | 1.1618 us |
| BitHacks | LegacyJitX64 | Random | 123.3894 us | 0.3052 us |
| Ternary | LegacyJitX64 | Const | 68.6997 us | 0.7440 us |
| BitHacks | LegacyJitX64 | Const | 123.0449 us | 0.7931 us |
| Ternary | RyuJitX64 | Random | 594.5310 us | 1.1537 us |
| BitHacks | RyuJitX64 | Random | 241.1466 us | 1.1446 us |
| Ternary | RyuJitX64 | Const | 179.7262 us | 0.4236 us |
| BitHacks | RyuJitX64 | Const | 240.8385 us | 0.7296 us |
| Ternary | Mono | Random | 203.6173 us | 1.7580 us |
| BitHacks | Mono | Random | 283.5624 us | 2.2254 us |
| Ternary | Mono | Const | 204.5277 us | 1.5814 us |
| BitHacks | Mono | Const | 282.5178 us | 1.9491 us |
Results in a nice form:
| Random | Const | |||
|---|---|---|---|---|
| Ternary | BitHacks | Ternary | BitHacks | |
| LegacyJIT-x86 | ≈643µs | ≈227µs | ≈160µs | ≈226µs |
| LegacyJIT-x64 | ≈450µs | ≈123µs | ≈68µs | ≈123µs |
| RyuJIT-x64 | ≈594µs | ≈241µs | ≈180µs | ≈241µs |
| Mono-x64 | ≈203µs | ≈283µs | ≈204µs | ≈282µs |
Analysis
First, let’s look at the right part of the table with const input. Here Ternary is always faster than BitHacks because it takes a small amount of instruction and the branch predictor works perfectly. For the random input on Full .NET Framework the BitHacks is faster for all JIT compilers. And there is an explanation for this: Ternary has a big performance penalty because it’s hard to predict the correct branch. Performance of BitHacks is the same for both input patterns and it also makes sense: this method doesn’t depend on branch predictor. However, we could also make a few interesting observation about Mono:
Ternaryworks faster thanBitHackseven on the random input.- Mono version of
Ternaryon the random input works much quicker than the same code on Full .NET Framework. - Mono shows the same performance for
TernaryandBitHacksfor both input arrays.
How is it possible? Let’s look at the asm. Here is the asm code for RyuJIT-x64:
; RyuJIT-x64
cmp ecx,edx ; check x < y
jl LESS
mov eax,edx ; return y
ret
LESS:
mov eax,ecx ; return x
ret
It looks very simple. How does it possible to rewrite this code and make it faster? Let’s think. The bottleneck here is the jl instruction which has a significant penalty because of the high-value misprediction rate. Is it possible to rewrite it without conditional jumps? Yes! Conditional move to the rescue!
; Mono4.6.2-x64
sub $0x18,%rsp
mov %rsi,(%rsp)
mov %rdi,0x8(%rsp)
mov %rcx,%rdi
mov %rdx,%rsi
cmp %esi,%edi
mov %rsi,%rax
cmovl %rdi,%rax ; Move if less (SF<>OF).
mov (%rsp),%rsi
mov 0x8(%rsp),%rdi
add $0x18,%rsp
retq
Here Mono uses the cmovl instruction (0F4C). So, it will not suffer from branch mispredictions because there is no branch on the asm level (despite we have a condition in the source C# code).
Conclusion
Thus, we can’t make a conclusion about MinTernary and MinBitHacks performance in general. It’s impossible to say which implementation is better for your problem without additional measurements because it depends on different conditions (like input data pattern and target runtime).
Is it a complete performance investigation? Of course, it’s not. We miss something in each component of our performance space:
- Source: We considered synthetic methods which calculate minimums in a special way. We easily can do small changes which significantly affect results.
- Data: We checked only two input patterns: a const pattern and a random pattern with a particular seed. If we take another input array (e.g. some data from real life), we get another performance picture.
- Environment: We didn’t check Linux and MacOS, CoreCLR, different versions of Mono, and so on. Also, we checked only Intel Core i7 Haswell; another processor micro-architectures have own characteristics of the branch predictor which is the bottleneck in this benchmark.
However, we get a good result: we have shown a part of performance space for target operations, and we have found relevant conditions which could affect the speed of our program. Note that it was just a benchmarking exercise, I wanted to show that there are a lot of troubles with benchmarking even in this simple case. Be careful with your performance measurements.