Finite-sample Gaussian efficiency: Quantile absolute deviation vs. Rousseeuw-Croux scale estimators
In this post, we discuss the finite-sample Gaussian efficiency of various robust dispersion estimators. The classic standard deviation has the highest possible Gaussian efficiency of $100\%$, but it is not robust: a single outlier can completely destroy the estimation. A typical robust alternative to the standard deviation is the Median Absolute Deviation ($\operatorname{MAD}$). While the $\operatorname{MAD}$ is highly robust (the breakdown point is $50\%$), it is not efficient: its asymptotic Gaussian efficiency is only $37\%$. Common alternative to the $\operatorname{MAD}$ is the Rousseeuw-Croux $S_n$ and $Q_n$ scale estimators that provide higher efficiency, keeping the breakdown point of $50\%$. In one of my recent preprints, I introduced the concept of the Quantile Absolute Deviation ($\operatorname{QAD}$) and its specific cases: the Standard Quantile Absolute Deviation ($\operatorname{SQAD}$) and the Optimal Quantile Absolute Deviation ($\operatorname{OQAD}$). Let us review the finite-sample and asymptotic values of the Gaussian efficiency for these estimators.
We start with reviewing the asymptotic Gaussian efficiency values:
| $\operatorname{SD}$ | $\operatorname{MAD}$ | RC $S_n$ | RC $Q_n$ | $\operatorname{SQAD}$ | $\operatorname{OQAD}$ | |
|---|---|---|---|---|---|---|
| Gaussian efficiency | $100\%$ | $37\%$ | $58\%$ | $82\%$ | $54\%$ | $65\%$ |
| Breakdown point | $0\%$ | $50\%$ | $50\%$ | $50\%$ | $32\%$ | $14\%$ |
As we can see, $Q_n$ looks like the best estimator: it has the efficiency of $82\%$ while its breakdown is $50\%$. In the asymptotic case, $\operatorname{SQAD}$ and $\operatorname{OQAD}$ do not look interesting: they are less efficient and less robust.
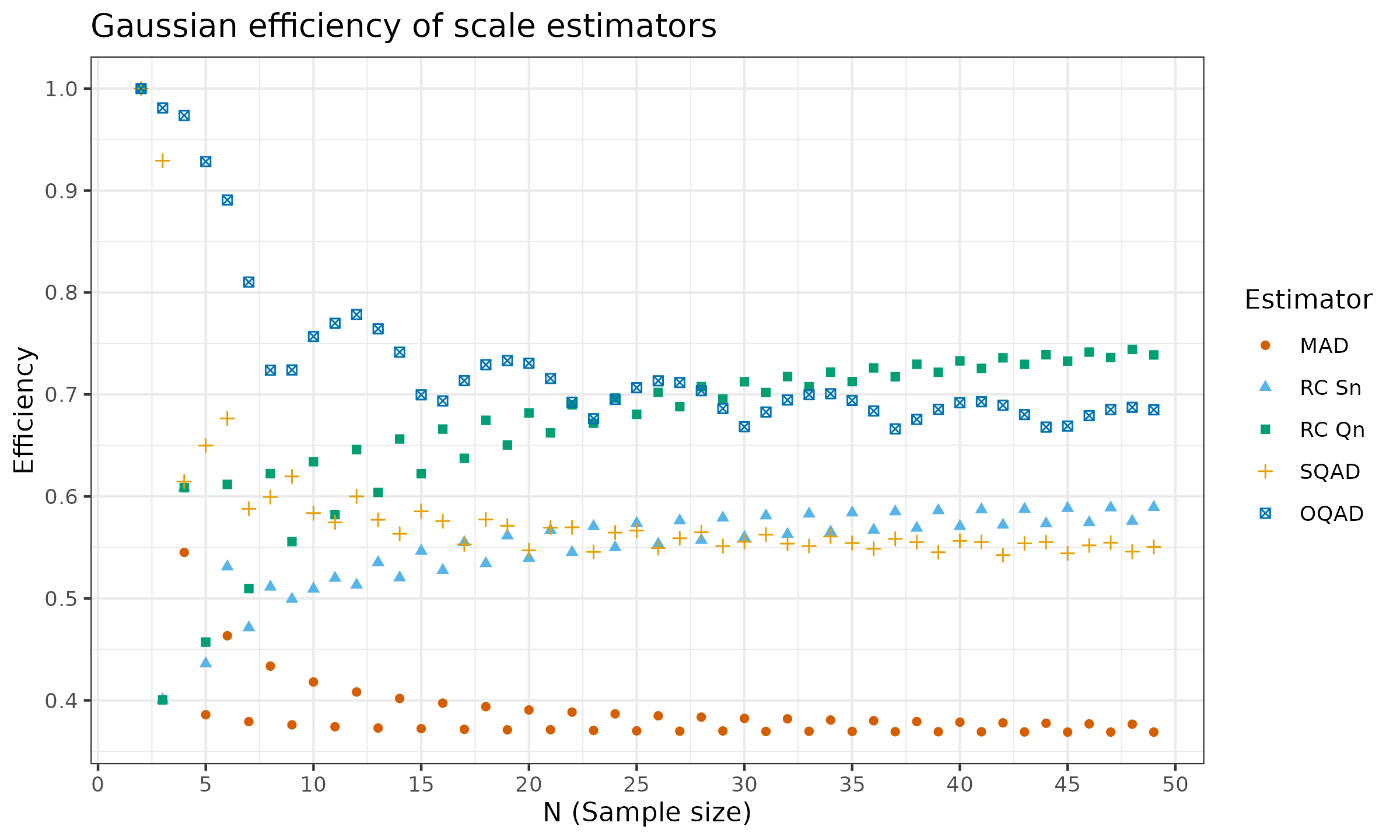
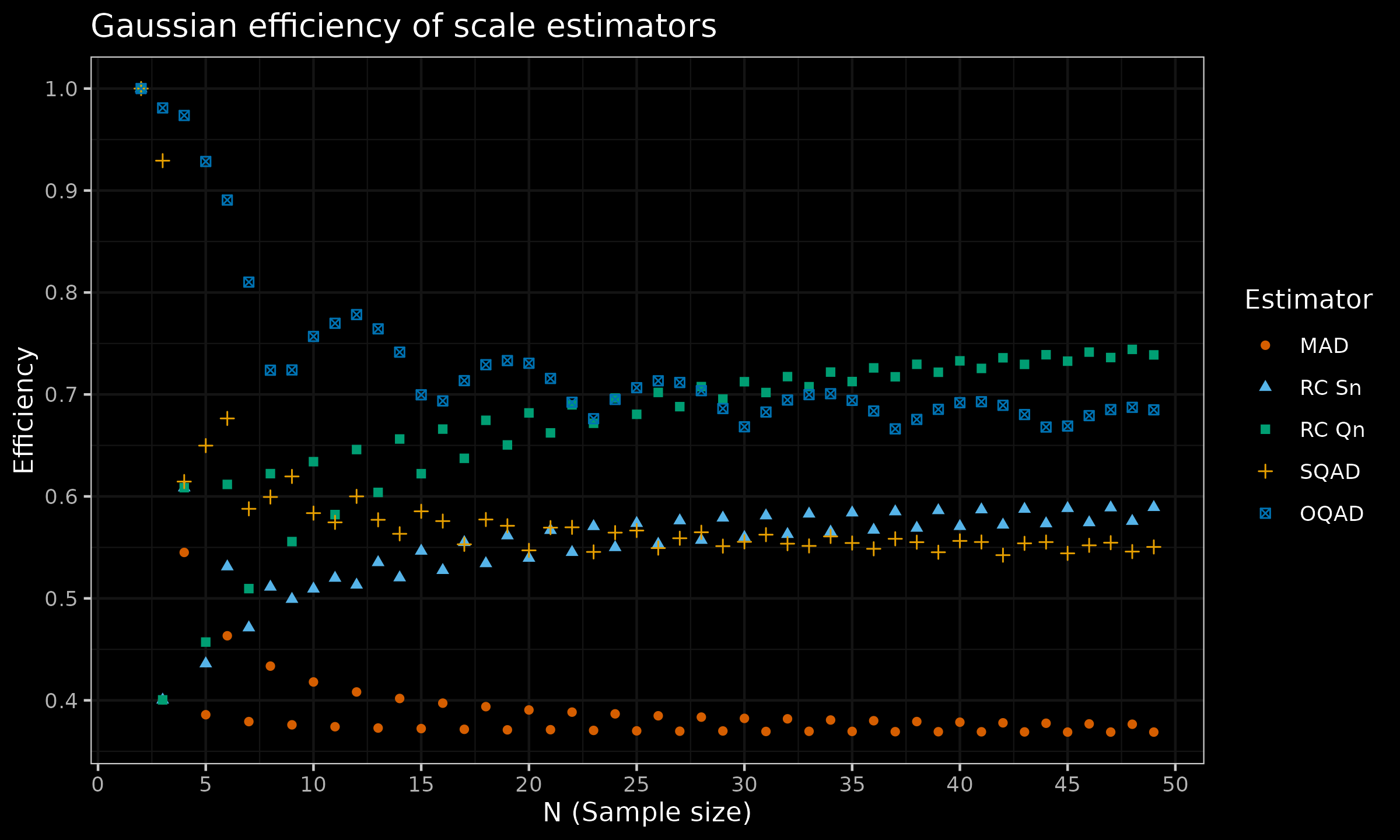
Now, let us check the finite-sample Gaussian efficiency values:
From this picture, we can see that $S_n$ and $Q_n$ are not so efficient in the case of a small sample. Meanwhile, $\operatorname{OQAD}$ is the most efficient estimator in this context for $n \leq 20$.
When we choose an estimator, it is important to check out not only its asymptotic properties, but also finite-sample properties that are evaluated for the target sample size.
References
- Andrey Akinshin (2022) “Quantile absolute deviation” arXiv:2208.13459
- Andrey Akinshin (2022) “Finite-sample Rousseeuw-Croux scale estimators” arXiv:2209.12268