Quantile-Respectful Density Estimation and Trimming
Update: this blog post is a part of research that aimed to build a quantile-respectful density estimation based on the Harrell-Davis quantile estimator. A preprint with the final results is available on arXiv: arXiv:2404.03835 [stat.ME]. Some information in this blog post can be obsolete: please, use the preprint as the primary reference.
I continue the topic of Quantile-Respectful Density Estimation in the context of Multimodality Detection. In this post, we briefly discuss the handling of the QRDE boundary spikes in order to correctly detect the near-border modes.
QRDE-HD has an issue in the form of boundary spikes, which may distort the multimodality detection procedure. Let us review two examples: the first one describes the problem, and the second one suggests a solution.
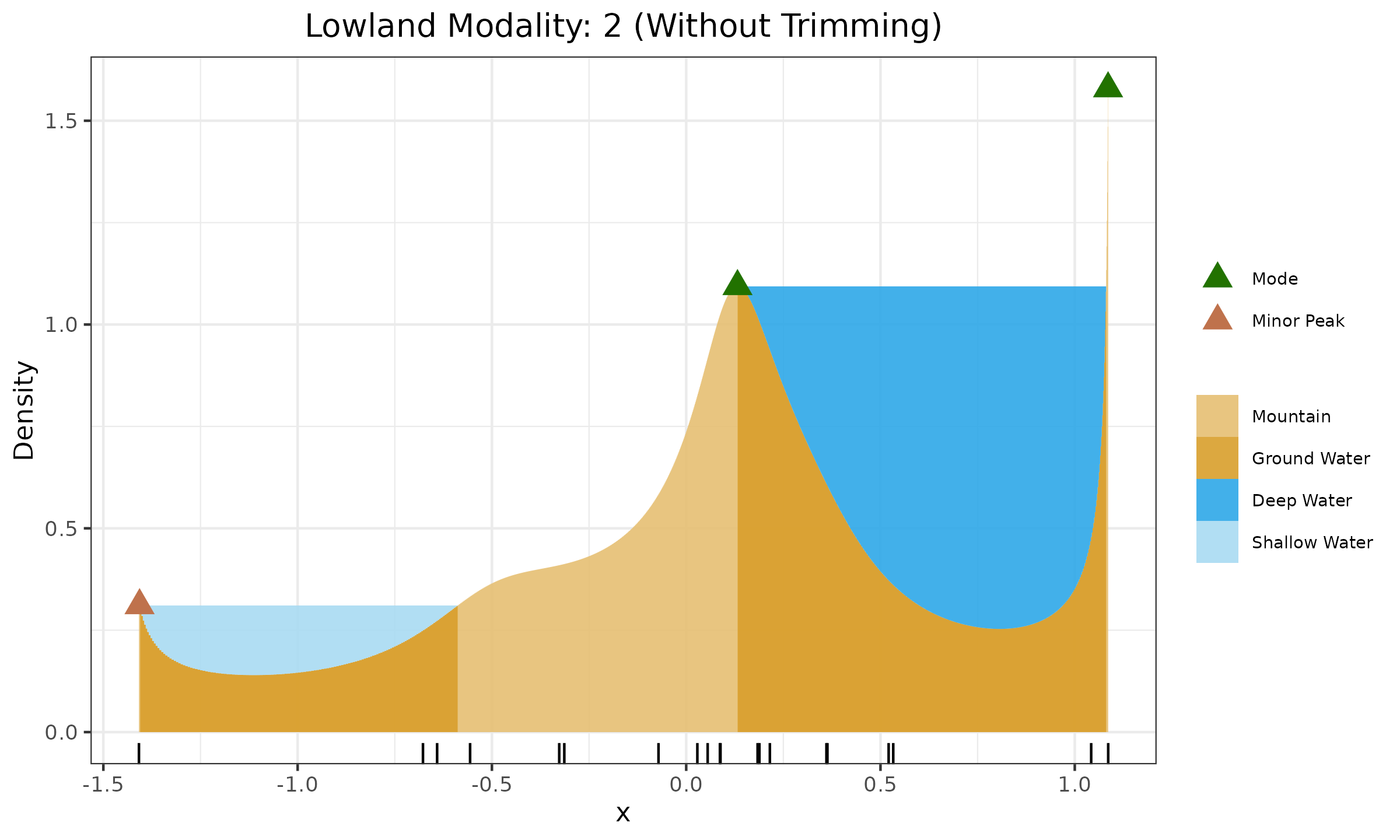
Let us review the lowland view for a sample of 20 elements from the standard normal distribution presented in the below figure:
As we can see, the right boundary spike was “recognized” as a mode, which leads to an incorrect insight into the number of modes.
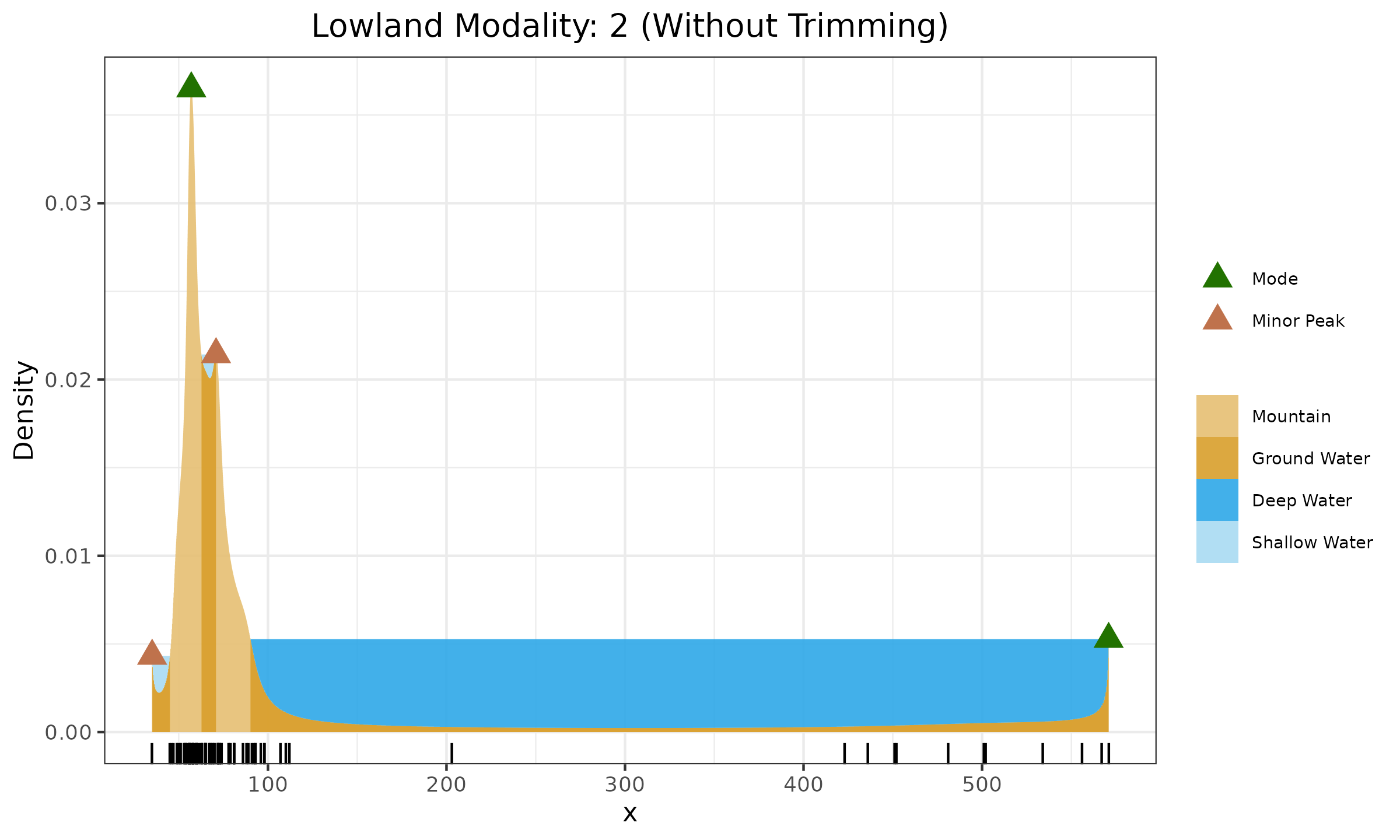
One may suggest just ignoring the boundary spikes. However, the boundary spikes may represent the actual modes. In the next figure, we can see a bimodal distribution with a right boundary spike.
In this case, two modes are detected correctly. If we always silently ignore the boundary spikes, it would distort the multimodality analysis for this case.
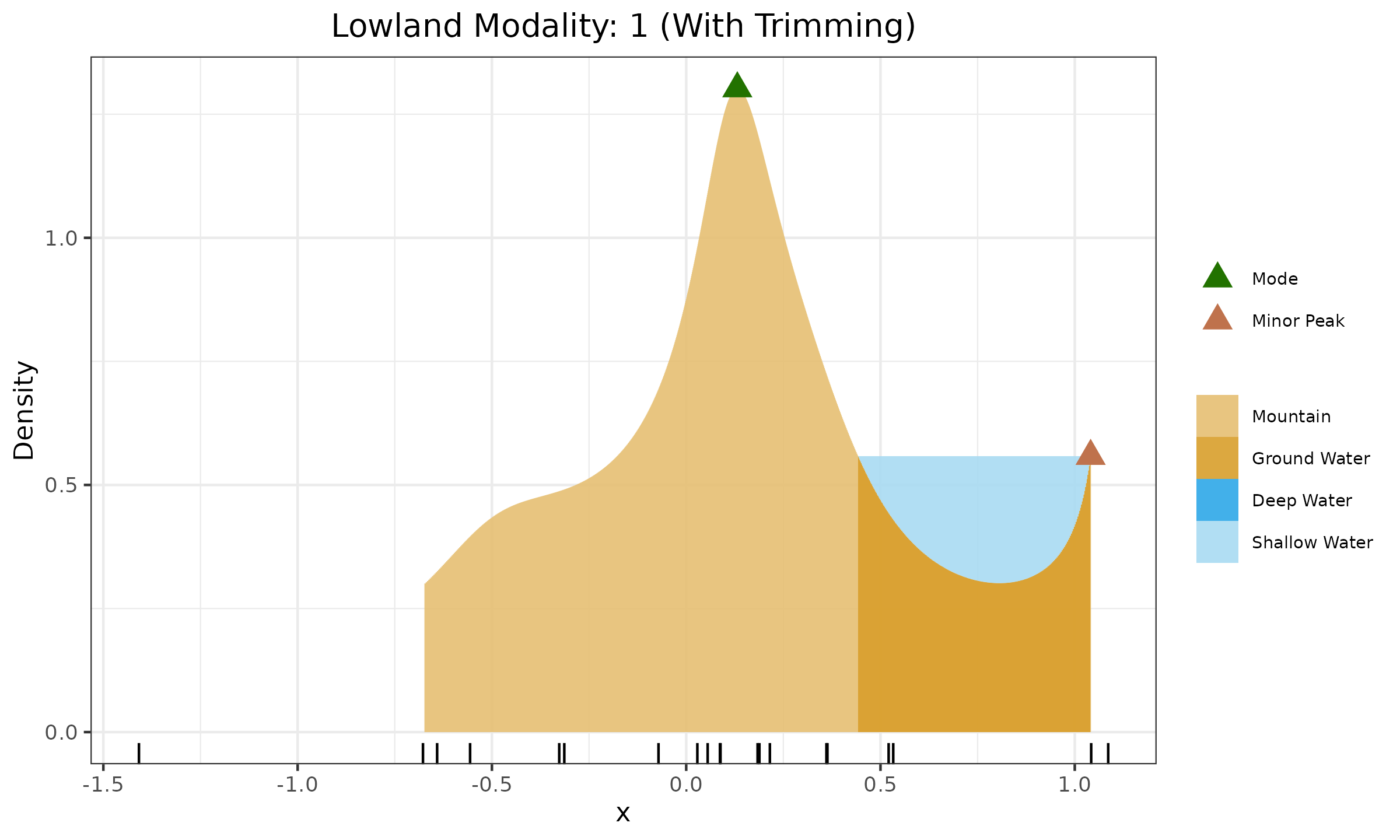
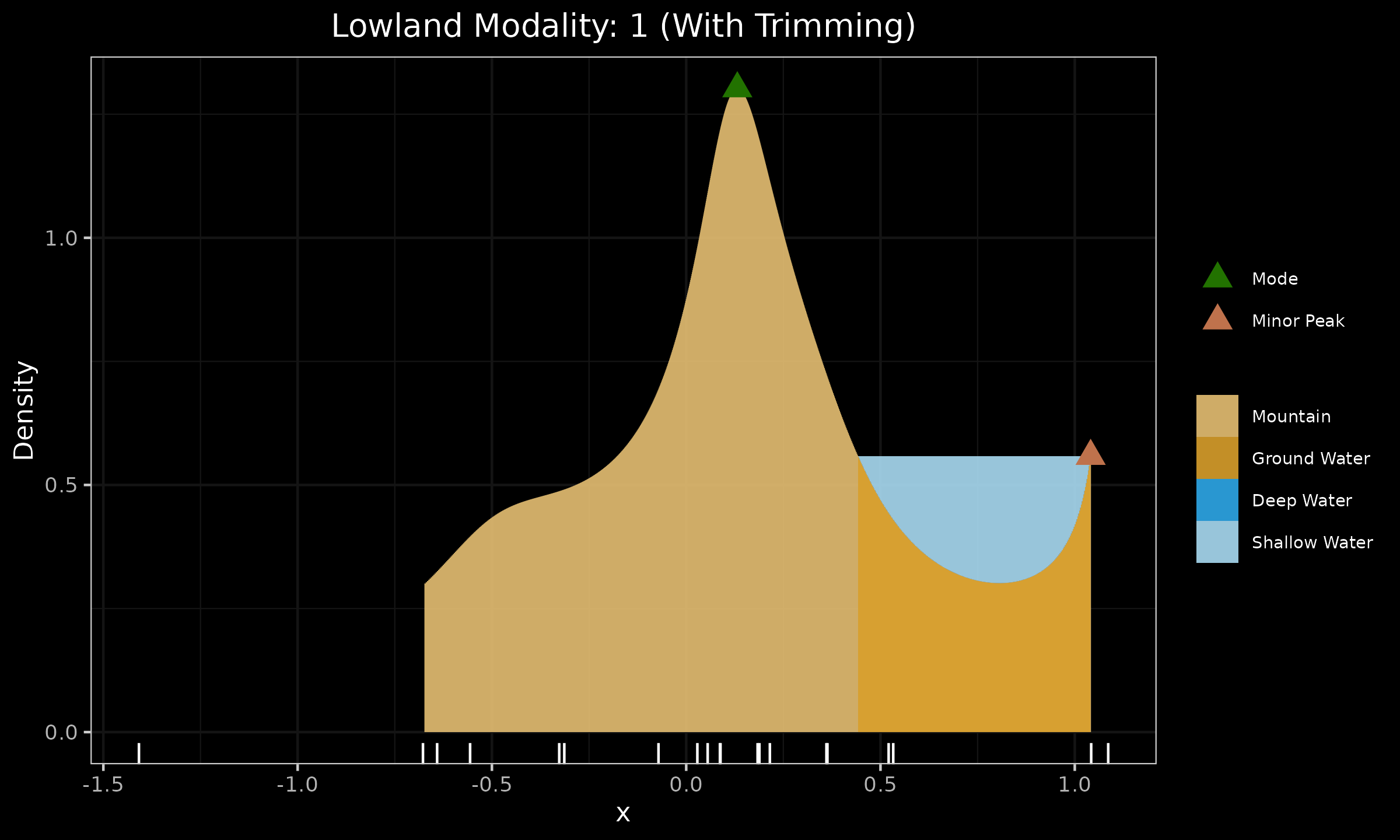
Instead of ignoring the boundary spikes, we suggest the trimming procedure. The “false” boundary spikes arise only in close proximity to the boundary elements due to the nature of the Harrell-Davis quantile estimator. If we exclude the minimum and the maximum sample element from the histogram range (while QRDE-HD is still built based on the full sample), the “false” boundary spikes will be suppressed. In the below figure, we can see that such a trimming procedure eliminates the false mode at the right boundary of the plot:
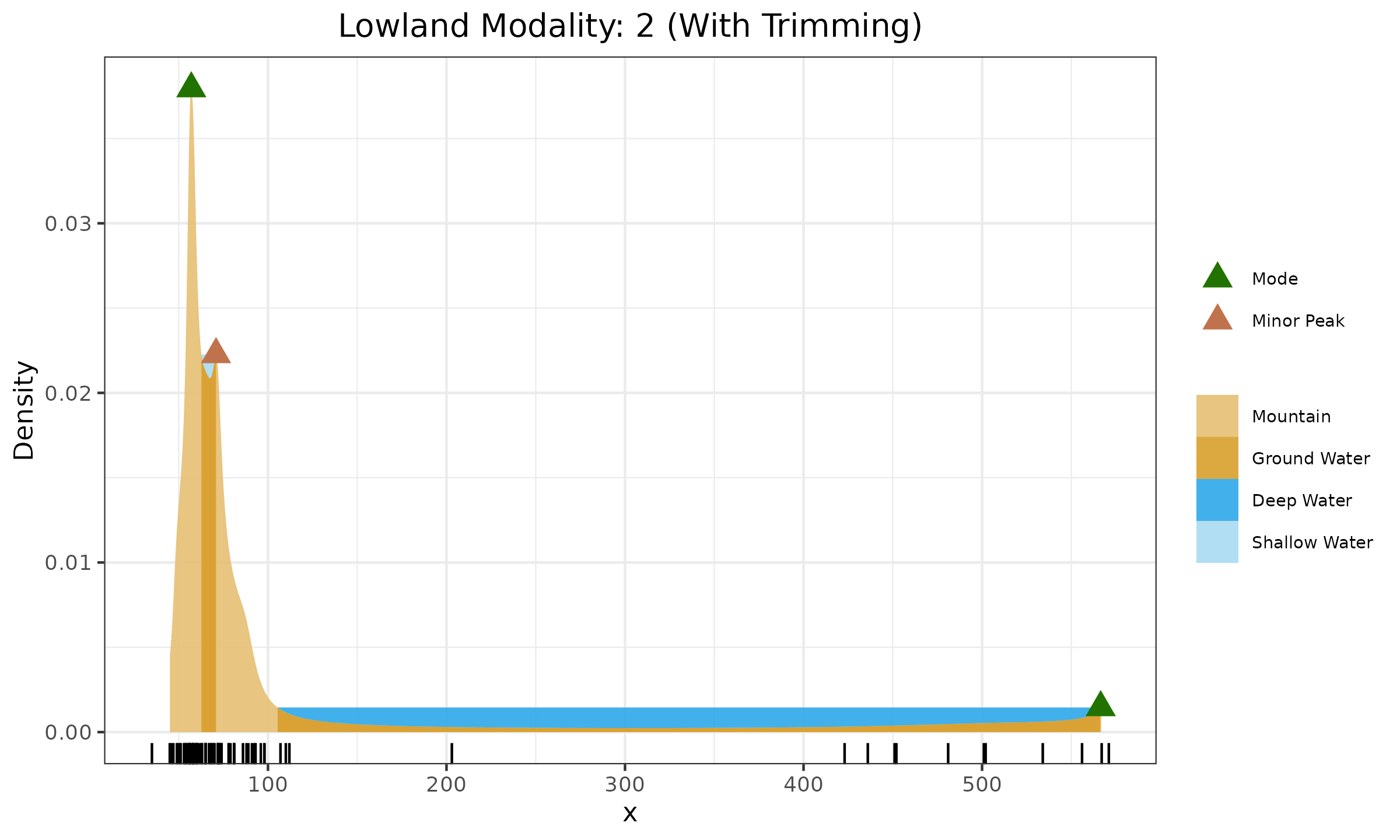
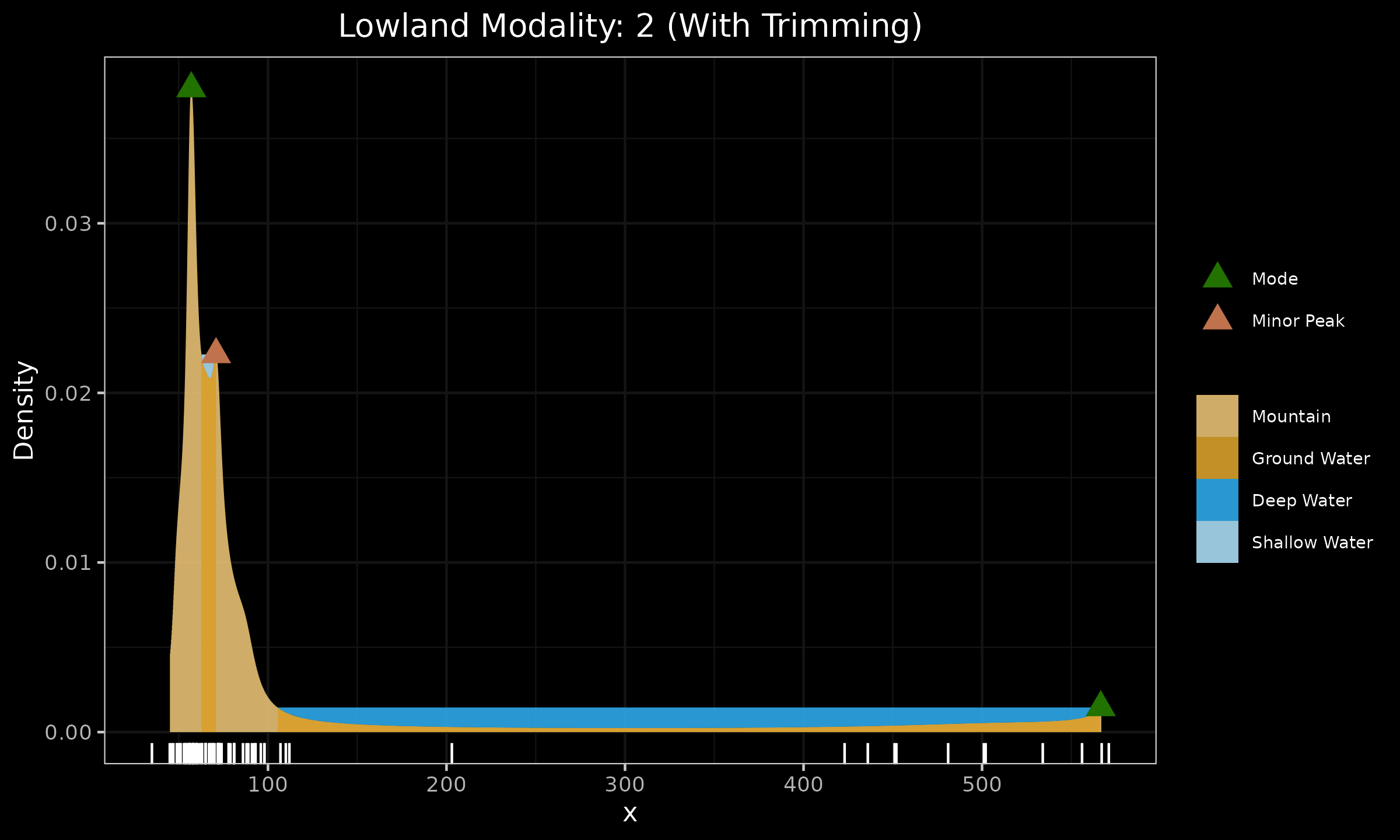
In the next figure, we can see that the trimming procedure does not affect the correct detection of the two modes in the bimodal case:
We believe that trimming a single element from each side is enough for the majority of cases. However, the number of trimmed elements may be increased if needed.