Four main books on robust statistics

Robust statistics is a practical and pragmatic branch of statistics. If you want to design reliable and trustworthy statistical procedures, the knowledge of robust statistics is essential. Unfortunately, it’s a challenging topic to learn.

In this post, I share my favorite books on robust statistics. I cannot pick my favorite one: each book is good in its own way, and all of them complement each other. I am returning to these books periodically to reinforce and expand my understanding of the topic.

Robust Statistics

Huber, Peter J., and Elvezio Ronchetti. Robust Statistics. 2nd ed. Wiley Series in Probability and Statistics. Hoboken, N.J: Wiley, 2009.
GoodReads Link Robust Statistics

It is one of the pioneer books in the field: the first edition was published in 1981. In this book (and his multiple other works), Peter J. Huber created a foundation for the further development of robust methods.

While I definitely recommend this book to everyone who wants to become an expert in robust statistics, I do not recommend it as the first book on this topic. The book is quite advanced and written for people with a strong mathematical background. For example, the first topic that is discussed just right after the introduction chapter is “The Weak Topology and its Metrization” (Levy, Prohorov, and the bounded Lipschitz metrics; Frechet and Gateaux derivatives; Hampel’s Theorem). This is an interesting and peculiar way to start discussing robust statistics. Most of the terms and notation symbols are assumed to be known by the reader, so the author doesn’t disturb you by providing definitions and explanations. The second edition has multiple improvements, but the book structure and style are the same.

Conclusion: the book is great but only for advanced readers; not for beginners.

Robust Statistics: The Approach Based on Influence Functions

Hampel, Frank R., Elevezio M. Ronchetti, Peter J. Rousseeuw, and Werner A. Stahel, eds. Robust Statistics: The Approach Based on Influence Functions. Digital print. Wiley Series in Probability and Mathematical Statistics Probability and Mathematical Statistics. New York: Wiley, 1986.
GoodReads Link Robust Statistics

This is another wonderful book about statistics. While it is also an advanced one, it is not as advanced as Huber’s book.

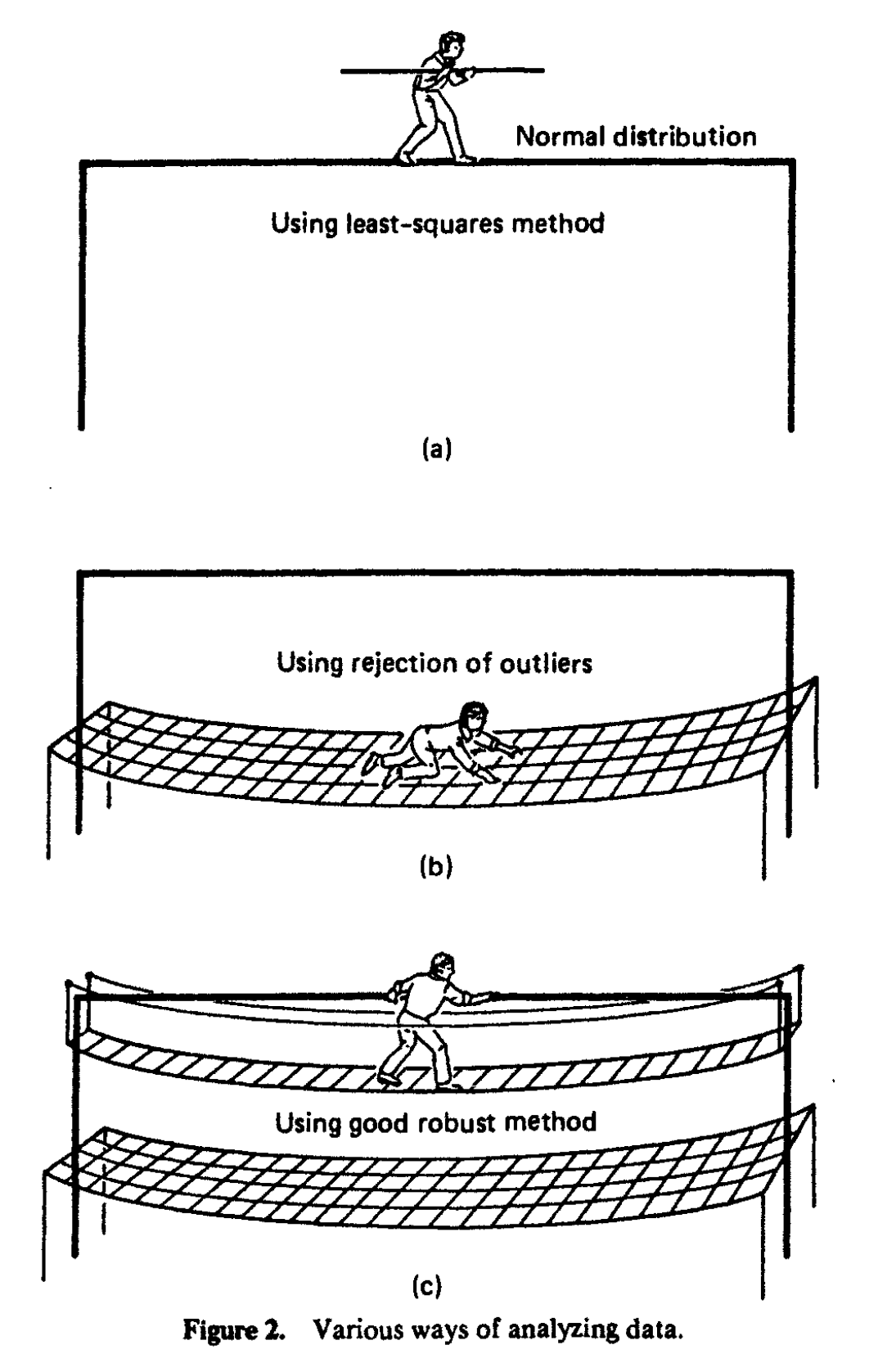
My favorite chapter is the first one: “Introduction and Motivation.” This is a 77-page read in which Hampel et al. set up the right mindset of using robust statistics. Just look at this picture from page 3 (click to enlarge):

The drawing is quite simple, but I feel so much love for the topic here. The authors had a valid option of writing a book without such illustrations (like most other mathematical books). But they deliberately decided to include such a picture in the book. The writing style is also quite friendly: sometimes it feels like a chat with a friend rather than like a mathematical textbook.

As you may guess from the title, the primary topic of the book is the influence functions. While these functions are discussed in most books on robust statistics, Frank R. Hampel is the person who introduced them. Unfortunately, not so many researchers nowadays actually use the influence functions to evaluate the properties of the selected estimators. I have to admit that this approach may be challenging to apply in some practical applications. If you, like me, do not always feel confident with using the influence functions, reading (or rereading) Hampel’s book is a great way to improve relevant skills!

Conclusion: the first chapter is recommended for everyone; the rest of the book is recommended for advanced readers.

Robust Statistics: Theory and Methods (with R)

Maronna, Ricardo A., R. Douglas Martin, Victor J. Yohai, and Matías Salibián-Barrera. Robust statistics: theory and methods (with R). Second edition. John Wiley & Sons, 2019. GoodReads Link Robust Statistics

The previous two books are great, but it is not an easy read for people who only start learning robust statistics. If you find the content of these books challenging to understand, I highly recommend “Robust Statistics: Theory and Methods (with R).” It is the most accessible book on the topic I know. Of course, the topic itself is an advanced one, so some mathematical background is still required. However, most not-so-trivial (and some trivial) things are well-explained.

Conclusion: recommended as the first book for beginners in robust statistics.

Introduction to Robust Estimation and Hypothesis Testing

Wilcox, Rand R. Introduction to Robust Estimation and Hypothesis Testing. 5th edition. Waltham, MA: Elsevier, 2021.
GoodReads Link Introduction to Robust Estimation and Hypothesis Testing

The topic of robust statistics claims to be practical. However, the three previous books may look too theoretical. While they discuss how to adapt mathematical tools to bizarre real-life data, they are too focused on the theoretical aspects of the suggested approaches. Sometimes, another reading session of another chapter leaves me in a confusing state. I think: “OK, all of this sounds fascinating and marvelous, but how do I solve my particular problem? Which method/approach/estimator/etc should I choose?”

At this moment, I open “Introduction to Robust Estimation and Hypothesis Testing” by Rand R. Wilcox. This is the most practical book about robust statistics. The theoretical part is reduced to the minimum: only the essential equations are presented. Instead of presenting the advanced stuff, references to relevant books and papers are provided. Such a format may be challenging for beginners: the knowledge of theoretical basis significantly simplifies the reading process.

However, if you know the basics, this is a wonderful handbook. It contains a broad overview of robust statistical tools. And it is not just a plain enumeration. For me, the most precious feature of this book is a plethora of small remarks regarding the real-life experience of suggested approaches. What kinds of pitfalls should we expect, what are the corner cases, which estimator is more efficient and when, and so on. The second most precious feature of this book is a set of reference R implementations for almost all the presented methods. If I’m curious about the actual behavior of the suggested estimator, I should not spend time implementing it from scratch: I can just take the ready implementation and start my experiments. In most cases, I use this book to get a brief overview of available approaches for the task I am working on.

Conclusion: recommended to engineers who are using robust statistics in real life.

Conclusion

In addition to multiple statistical papers, these four books have been key to my study of robust statistics. I find it beneficial to revisit sections of these texts every several months. Each reading deepens the understanding and uncovers nuances that might have been missed during previous readings.

I hope these resources will be as valuable to you in your study of robust statistics as they have been to me.