Finite-sample efficiency of the Rousseeuw-Croux estimators

The Rousseeuw-Croux $S_n$ and $Q_n$ estimators are robust and efficient measures of scale. Their breakdown points are equal to $0.5$ which is also the breakdown point of the median absolute deviation (MAD). However, their statistical efficiency values are much better than the efficiency of MAD. To be specific, the MAD asymptotic relative Gaussian efficiency against the standard deviation is about $37\%$, whereas the corresponding values for $S_n$ and $Q_n$ are $58\%$ and $82\%$ respectively. Although these numbers are quite impressive, they are only asymptotic values. In practice, we work with finite samples. And the finite-sample efficiency could be much lower than the asymptotic one. In this post, we perform a simulation study in order to obtain the actual finite-sample efficiency values for these two estimators.

Introduction

The $S_n$ and $Q_n$ estimators are presented in rousseeuw1993. For a sample $x = \{ x_1, x_2, \ldots, x_n \}$, they are defined as follows:

$$ S_n = c_n \cdot 1.1926 \cdot \operatorname{lowmed}_i \; \operatorname{highmed}_j \; |x_i - x_j|, $$$$ Q_n = d_n \cdot 2.2191 \cdot \{ |x_i-x_j|; i < j \}_{(k)}, $$

where

• $\operatorname{lowmed}$ is the $\lfloor (n+1) / 2 \rfloor^\textrm{th}$ order statistic out of $n$ numbers,
• $\operatorname{highmed}$ is the $(\lfloor n / 2 \rfloor + 1)^\textrm{th}$ order statistic out of $n$ numbers,
• $c_n$, $d_n$ are bias-correction factors for finite samples (some approximation can be found in [Rousseeuw1993]),
• $k = \binom{\lfloor n / 2 \rfloor + 1}{2}$,
• ${}_{(k)}$ is the $k^\textrm{th}$ order statistic.

In this post, we also use the unbiased standard deviation which is defined as follows:

$$ s_n = \sqrt{\frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^2} \bigg/ c_4(n), \quad c_4(n) = \sqrt{\frac{2}{n-1}}\frac{\Gamma(\frac{n}{2})}{\Gamma(\frac{n-1}{2})}. $$

The median absolute deviation uses the bias-correction factors presented in [Akinshin2022].

Relative efficiency

In order to evaluate the relative statistical efficiency against the standard deviation under normality, we perform the following simulation study:

• Enumerate various sample sizes $n$ between $3$ and $200$.
• For each sample size $n$, generate $300\,000$ random samples from the standard normal distribution.
• For each sample, estimate $s_n$, $\operatorname{MAD}_n$, $S_n$, $Q_n$.
• For each $n$, calculate the relative statistical efficiency of $\operatorname{MAD}_n$, $S_n$, $Q_n$ against $s_n$ as $e(T_n) = \mathbb{V}(s_n) / \mathbb{V}(T_n)$.

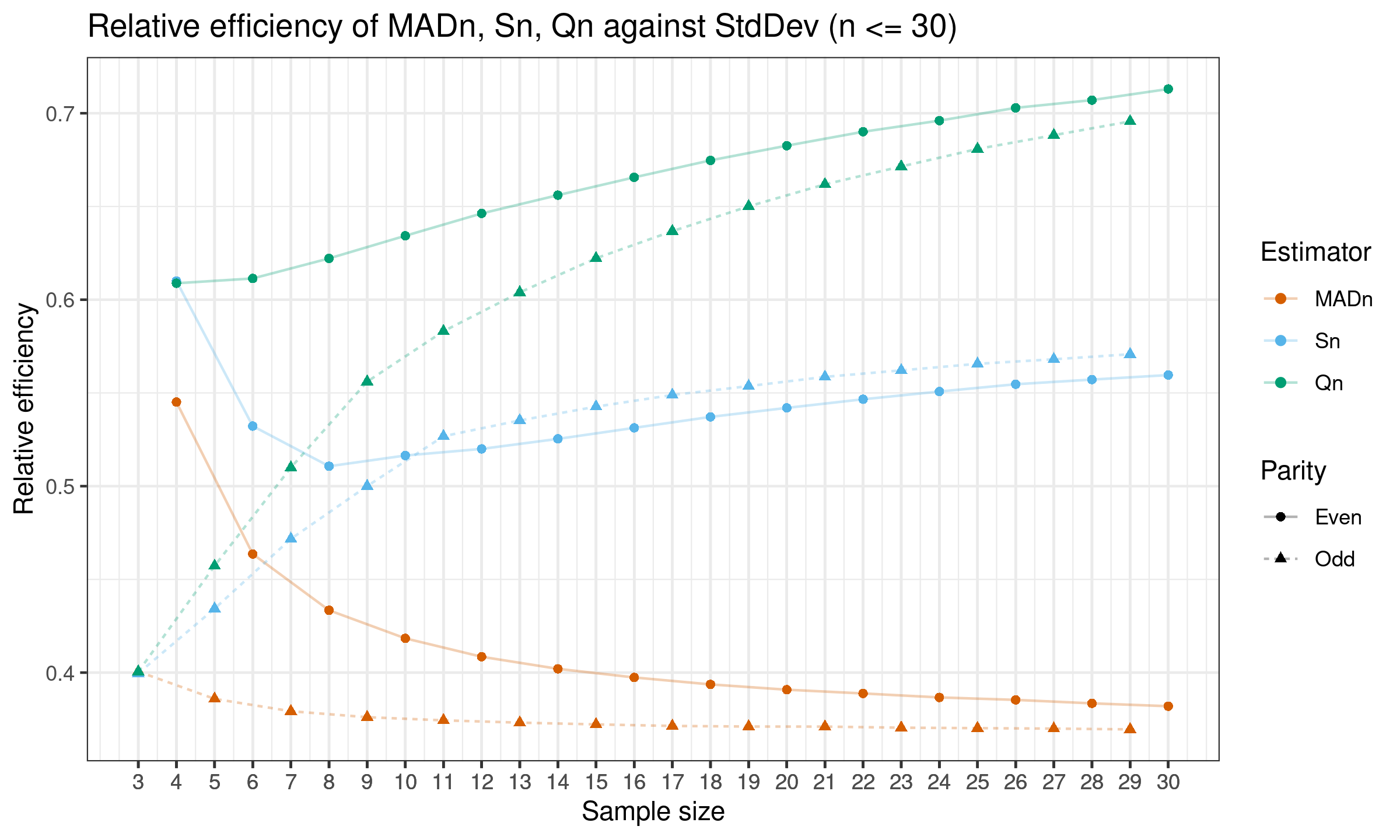
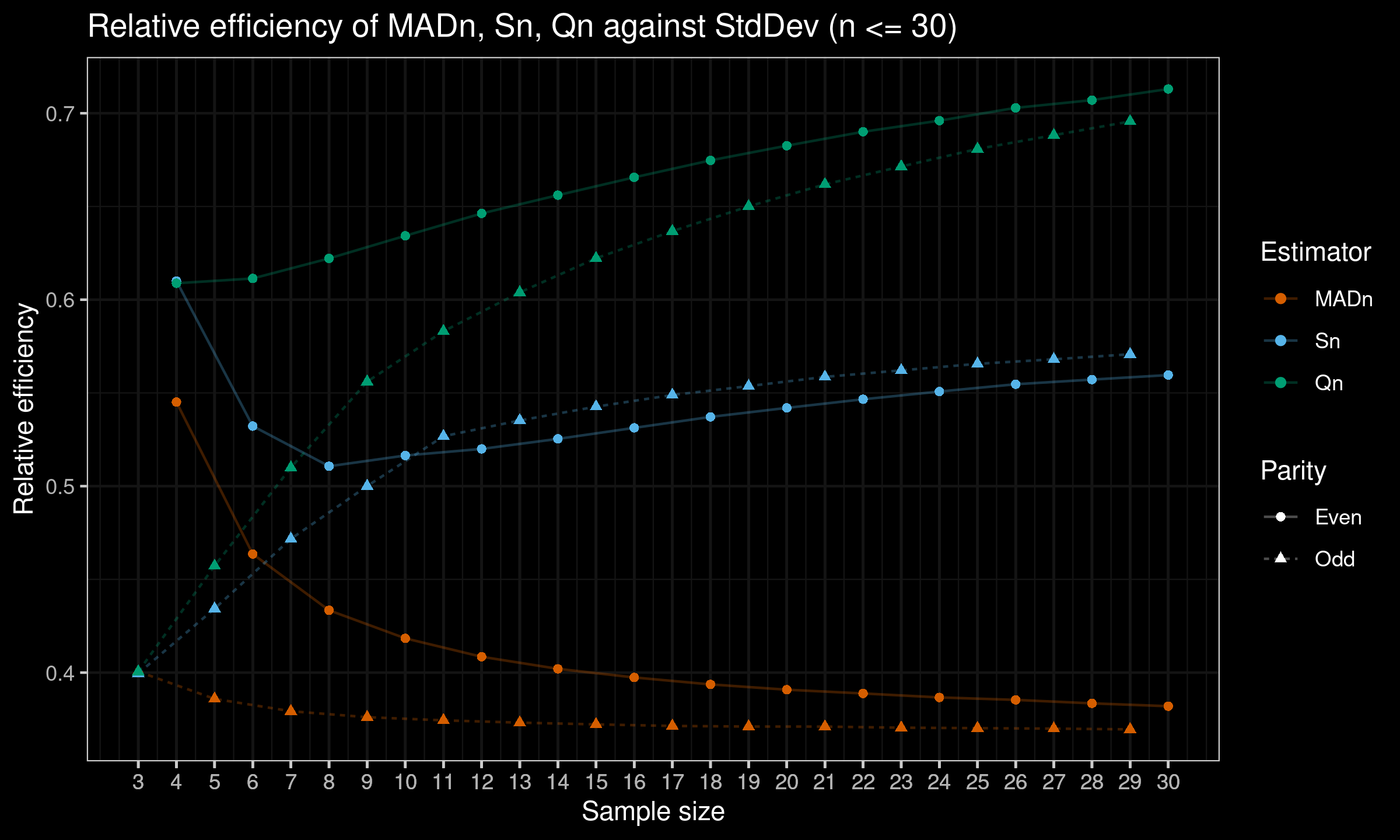
Here is the plot with results for $n \leq 30$:

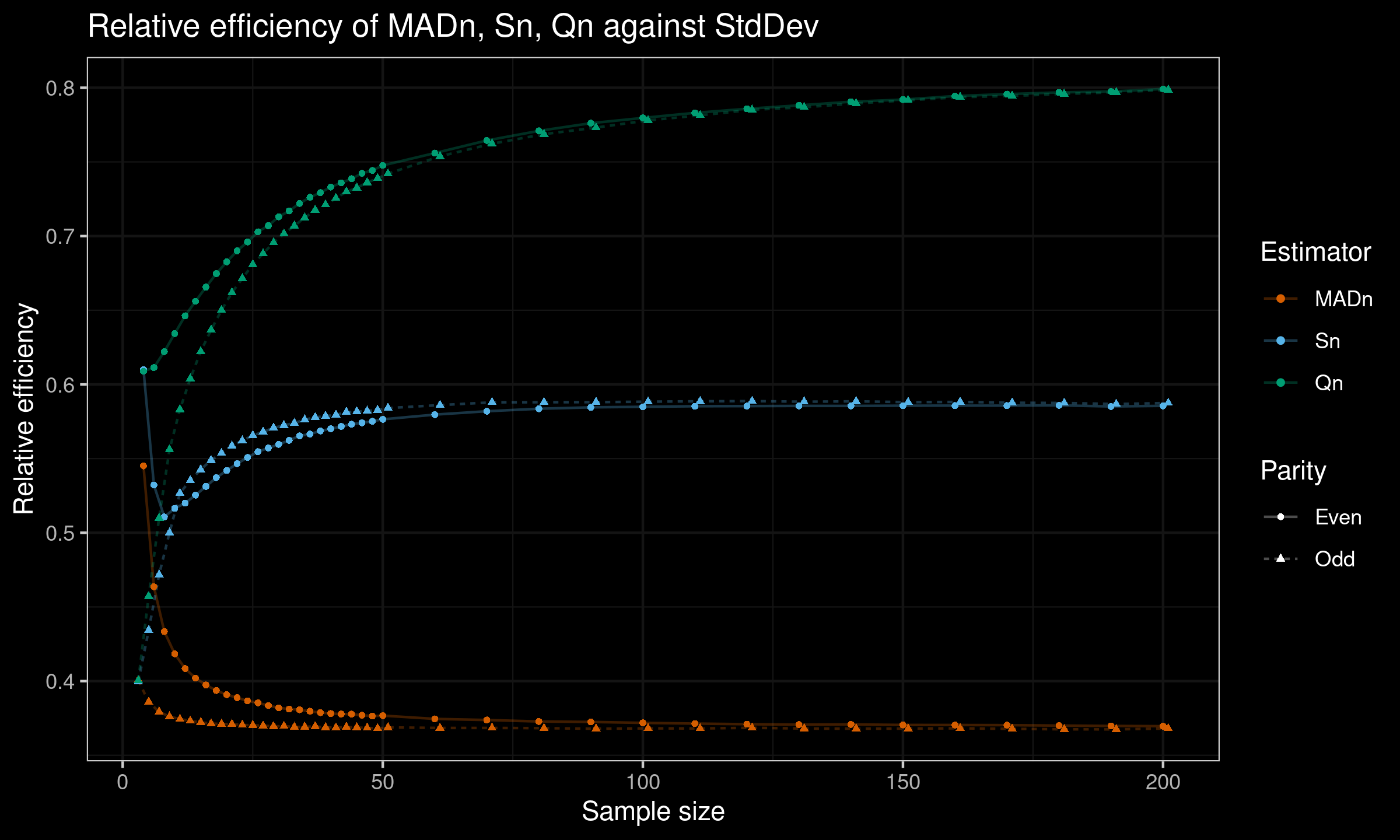
Here is the plot with all the results:

And here is a table with raw results:

n	MADn	Sn	Qn
3	0.40056	0.39961	0.40050
4	0.54508	0.61005	0.60883
5	0.38591	0.43430	0.45723
6	0.46360	0.53221	0.61139
7	0.37928	0.47172	0.50996
8	0.43342	0.51068	0.62214
9	0.37609	0.50004	0.55606
10	0.41836	0.51644	0.63429
11	0.37439	0.52677	0.58308
12	0.40849	0.51998	0.64626
13	0.37316	0.53525	0.60392
14	0.40201	0.52536	0.65607
15	0.37222	0.54263	0.62221
16	0.39739	0.53126	0.66562
17	0.37139	0.54889	0.63675
18	0.39366	0.53715	0.67473
19	0.37107	0.55365	0.65006
20	0.39082	0.54198	0.68261
21	0.37103	0.55860	0.66187
22	0.38881	0.54660	0.69007
23	0.37045	0.56210	0.67145
24	0.38668	0.55075	0.69604
25	0.37021	0.56561	0.68085
26	0.38536	0.55466	0.70290
27	0.36995	0.56805	0.68823
28	0.38350	0.55716	0.70705
29	0.36956	0.57074	0.69561
30	0.38197	0.55959	0.71301
31	0.36961	0.57241	0.70165
32	0.38113	0.56236	0.71696
33	0.36911	0.57396	0.70695
34	0.38071	0.56534	0.72204
35	0.36918	0.57624	0.71234
36	0.37966	0.56656	0.72613
37	0.36942	0.57783	0.71760
38	0.37876	0.56863	0.72929
39	0.36880	0.57860	0.72118
40	0.37813	0.57007	0.73307
41	0.36864	0.57944	0.72553
42	0.37778	0.57167	0.73592
43	0.36902	0.58136	0.72991
44	0.37771	0.57314	0.73867
45	0.36872	0.58165	0.73254
46	0.37698	0.57415	0.74231
47	0.36845	0.58213	0.73608
48	0.37643	0.57513	0.74428
49	0.36810	0.58270	0.73894
50	0.37673	0.57648	0.74764
51	0.36879	0.58407	0.74207
60	0.37452	0.57965	0.75597
61	0.36842	0.58606	0.75376
70	0.37376	0.58194	0.76447
71	0.36843	0.58793	0.76228
80	0.37277	0.58361	0.77094
81	0.36827	0.58799	0.76872
90	0.37247	0.58455	0.77612
91	0.36790	0.58805	0.77317
100	0.37184	0.58492	0.77968
101	0.36814	0.58838	0.77800
110	0.37137	0.58529	0.78308
111	0.36806	0.58864	0.78142
120	0.37093	0.58538	0.78582
121	0.36853	0.58878	0.78514
130	0.37063	0.58551	0.78816
131	0.36800	0.58835	0.78685
140	0.37080	0.58553	0.79057
141	0.36793	0.58861	0.78943
150	0.37045	0.58567	0.79202
151	0.36798	0.58804	0.79157
160	0.37040	0.58572	0.79443
161	0.36817	0.58822	0.79363
170	0.37031	0.58572	0.79571
171	0.36781	0.58766	0.79449
180	0.37001	0.58590	0.79686
181	0.36751	0.58749	0.79582
190	0.36977	0.58513	0.79752
191	0.36747	0.58678	0.79695
200	0.36960	0.58556	0.79917
201	0.36806	0.58749	0.79857

Conclusion

As we can see, on small samples relative efficiency of $S_n$ and $Q_n$ are still better than the efficiency of $\operatorname{MAD}_n$, but it is much lower than the asymptotic values.

References

• [Rousseeuw1992]
  Croux, Christophe, and Peter J. Rousseeuw. “Time-Efficient Algorithms for Two Highly Robust Estimators of Scale.” In Computational Statistics, edited by Yadolah Dodge and Joe Whittaker, 411–28. Heidelberg: Physica-Verlag HD, 1992.
  https://doi.org/10.1007/978-3-662-26811-7_58
• [Rousseeuw1993]
  Rousseeuw, Peter J., and Christophe Croux. “Alternatives to the Median Absolute Deviation.” Journal of the American Statistical Association 88, no. 424 (December 1, 1993): 1273–83.
  https://doi.org/10.1080/01621459.1993.10476408
• [Akinshin2022]
  Andrey Akinshin (2022) “Finite-sample bias-correction factors for the median absolute deviation based on the Harrell-Davis quantile estimator and its trimmed modification,” arXiv:2207.12005