Finite-sample Gaussian efficiency: Shamos vs. Rousseeuw-Croux Qn scale estimators
Previously, we compared the finite-sample Gaussian efficiency of the Rousseeuw-Croux scale estimators and the QAD estimator. In this post, we compare the finite-sample Gaussian efficiency of the Shamos scale estimator and the Rousseeuw-Croux $Q_n$ scale estimator. This is a particularly interesting comparison. In the famous “Alternatives to the Median Absolute Deviation” (1993) paper by Peter J. Rousseeuw and Christophe Croux, the authors presented $Q_n$ as an improved version of the Shamos estimator. Both estimators are based on the set of pairwise absolute differences between the elements of the sample. The Shamos estimator takes the median of this set and, therefore, has the asymptotic breakdown point of $\approx 29\%$ and the asymptotic Gaussian efficiency of $\approx 86\%$. $Q_n$ takes the first quartile of this set and, therefore, has the asymptotic breakdown point of $\approx 50\%$ (like the median) and the asymptotic Gaussian efficiency of $\approx 82\%$. It sounds like a good deal: we trade $4\%$ of the asymptotic Gaussian efficiency for $21\%$ of the asymptotic breakdown point. What could possibly stop us from using $Q_n$ everywhere instead of the Shamos estimator?
Well, here is a trick. The breakdown point of $29\%$ is actually a practically reasonable value. If more than $29\%$ of the sample are outliers, we should probably consider them not as outliers but as a separate mode. Such a situation should be handled by a multimodality detector and lead us to a different approach. The usage of dispersion estimators in the case of multimodal distributions is potentially misleading. When such a multimodality diagnostic scheme is used, there is no practical need for a higher breakdown point.
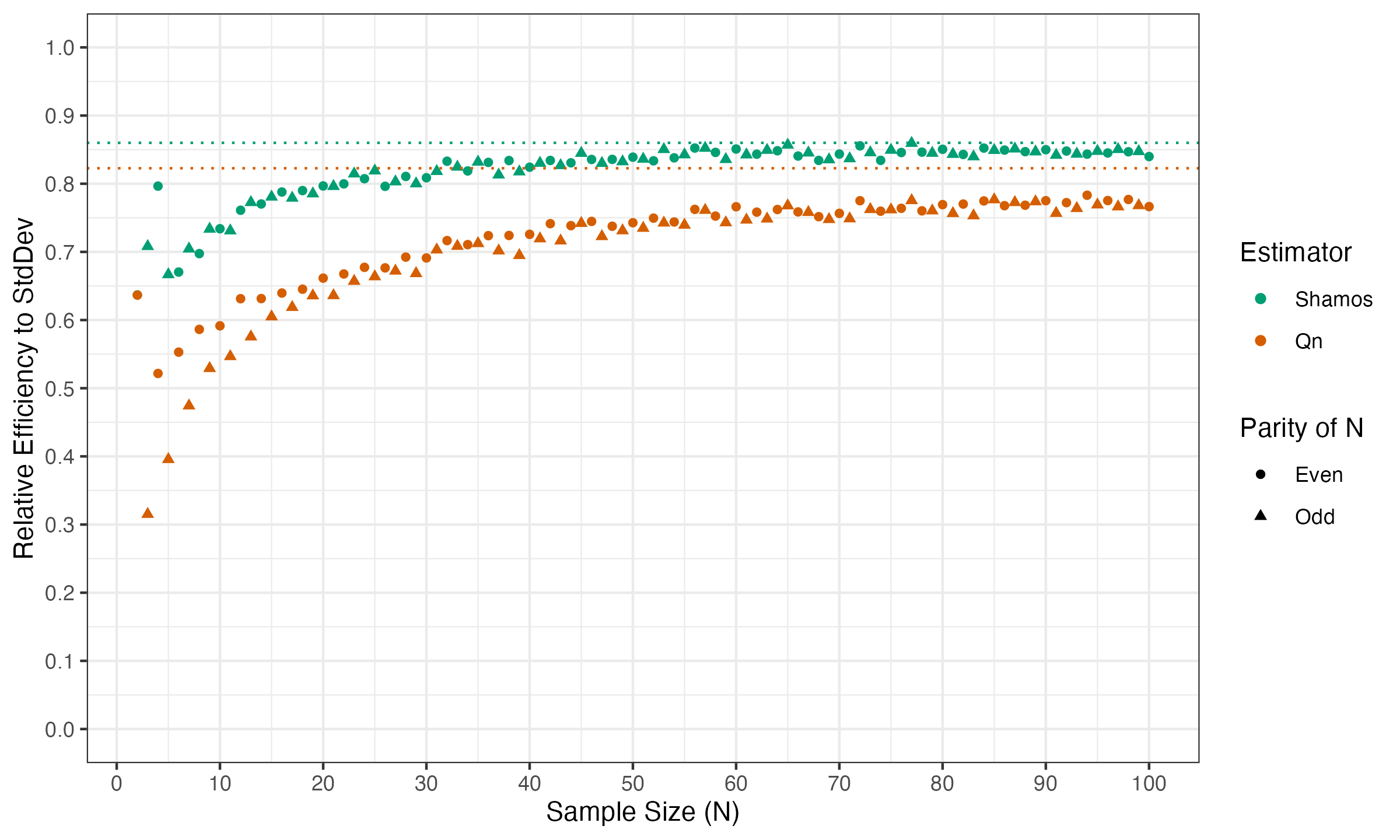
Thus, the breakdown point of $50\%$ is not so impressive property of $Q_n$. Meanwhile, the drop in Gaussian efficiency is not so enjoyable. $4\%$ may sound like a negligible difference, but it is only the asymptotic value. In real life, we typically tend to work with finite samples. Let us explore the actual finite-sample Gaussian efficiency values of these estimators.
While the asymptotic gap of $4\%$ is indeed small, the finite-sample gap is much more significant. Even for $n=4$ the gap is about $7\%$ ($84\%$ vs. $77\%$). For small samples, the gap magnitude can be quite dramatic. Here are the values for $3 \leq n \leq 20$:
| n | shamos | qn | gap |
|---|---|---|---|
| 3 | 0.708 | 0.317 | 0.392 |
| 4 | 0.790 | 0.516 | 0.273 |
| 5 | 0.656 | 0.400 | 0.256 |
| 6 | 0.680 | 0.556 | 0.124 |
| 7 | 0.704 | 0.469 | 0.235 |
| 8 | 0.710 | 0.579 | 0.130 |
| 9 | 0.732 | 0.524 | 0.208 |
| 10 | 0.741 | 0.599 | 0.141 |
| 11 | 0.737 | 0.553 | 0.184 |
| 12 | 0.755 | 0.615 | 0.140 |
| 13 | 0.765 | 0.579 | 0.186 |
| 14 | 0.764 | 0.629 | 0.134 |
| 15 | 0.774 | 0.601 | 0.174 |
| 16 | 0.780 | 0.642 | 0.138 |
| 17 | 0.778 | 0.616 | 0.163 |
| 18 | 0.786 | 0.652 | 0.134 |
| 19 | 0.791 | 0.635 | 0.157 |
| 20 | 0.794 | 0.664 | 0.130 |
Based on these observations, it seems that the Shamos estimator has a higher potential to be practically useful than $Q_n$ (especially on small samples!).