Sheather & Jones vs. unbiased cross-validation

In the post about the importance of kernel density estimation bandwidth, I reviewed several bandwidth selectors and showed their impact on the KDE. The classic selectors like Scott’s rule of thumb or Silverman’s rule of thumb are designed for the normal distribution and perform purely in non-parametric cases. One of the most significant caveats is that they can mask multimodality. The same problem is also relevant to the biased cross-validation method. Among all the bandwidth selectors available in R, only Sheather & Jones and unbiased cross-validation provide reliable results in the multimodal case. However, I always advocate using the Sheather & Jones method rather than the unbiased cross-validation approach.

In this post, I will show the drawbacks of the unbiased cross-validation method and what kind of problems we can get if we use it as a KDE bandwidth selector.

Multimodality

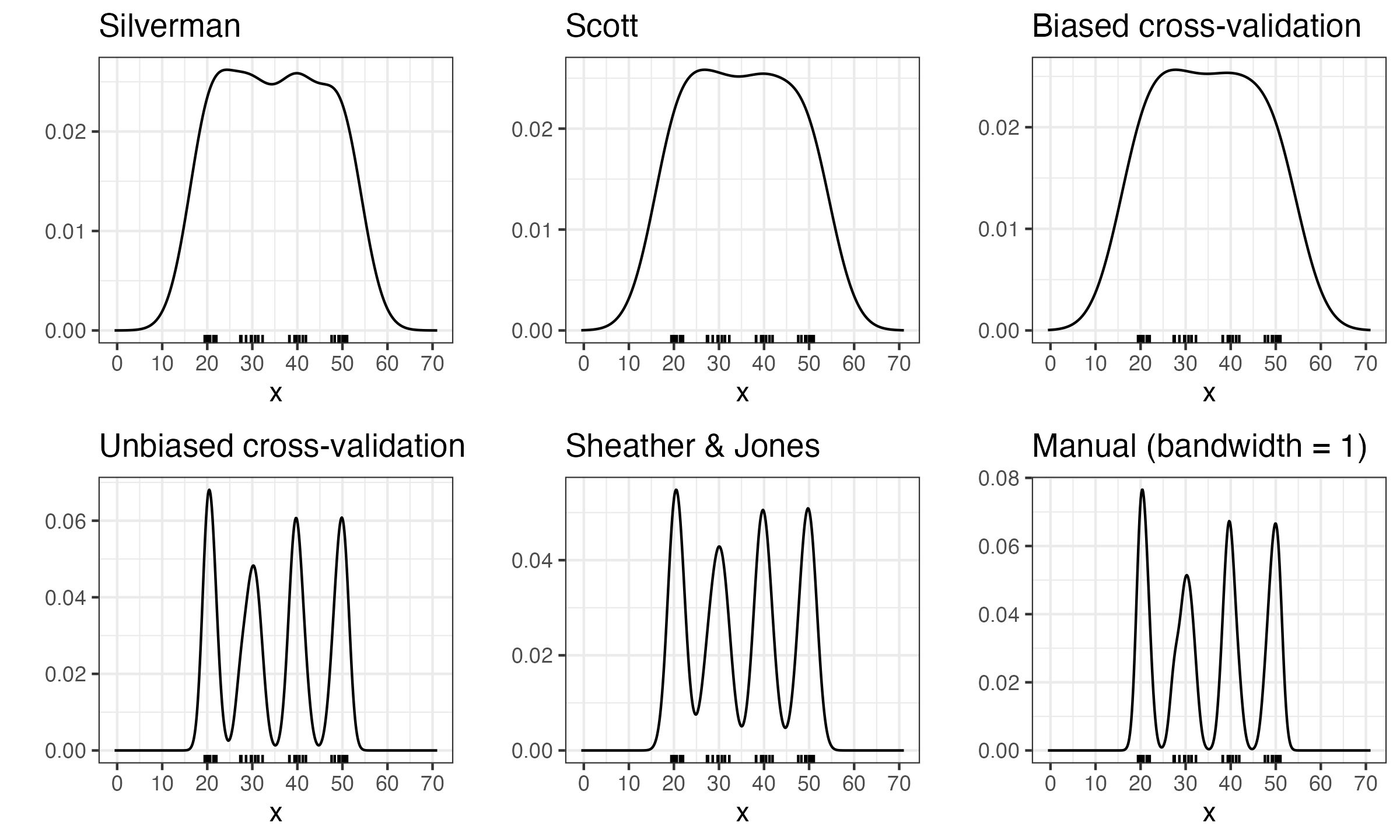
First of all, let us recall the multimodality problem. We consider a distribution with four modes:

$$ 0.25 \cdot \mathcal{N}(20, 1) + 0.25 \cdot \mathcal{N}(30, 1) + 0.25 \cdot \mathcal{N}(40, 1) + 0.25 \cdot \mathcal{N}(50, 1). $$

For this distribution, we build KDEs using various bandwidth selectors:

As we can see, only Sheather & Jones and unbiased cross-validation can present the true nature of the distribution multimodality among the presented selectors. So, how should we choose between these two selectors? Here we need one more example.

Wobbliness

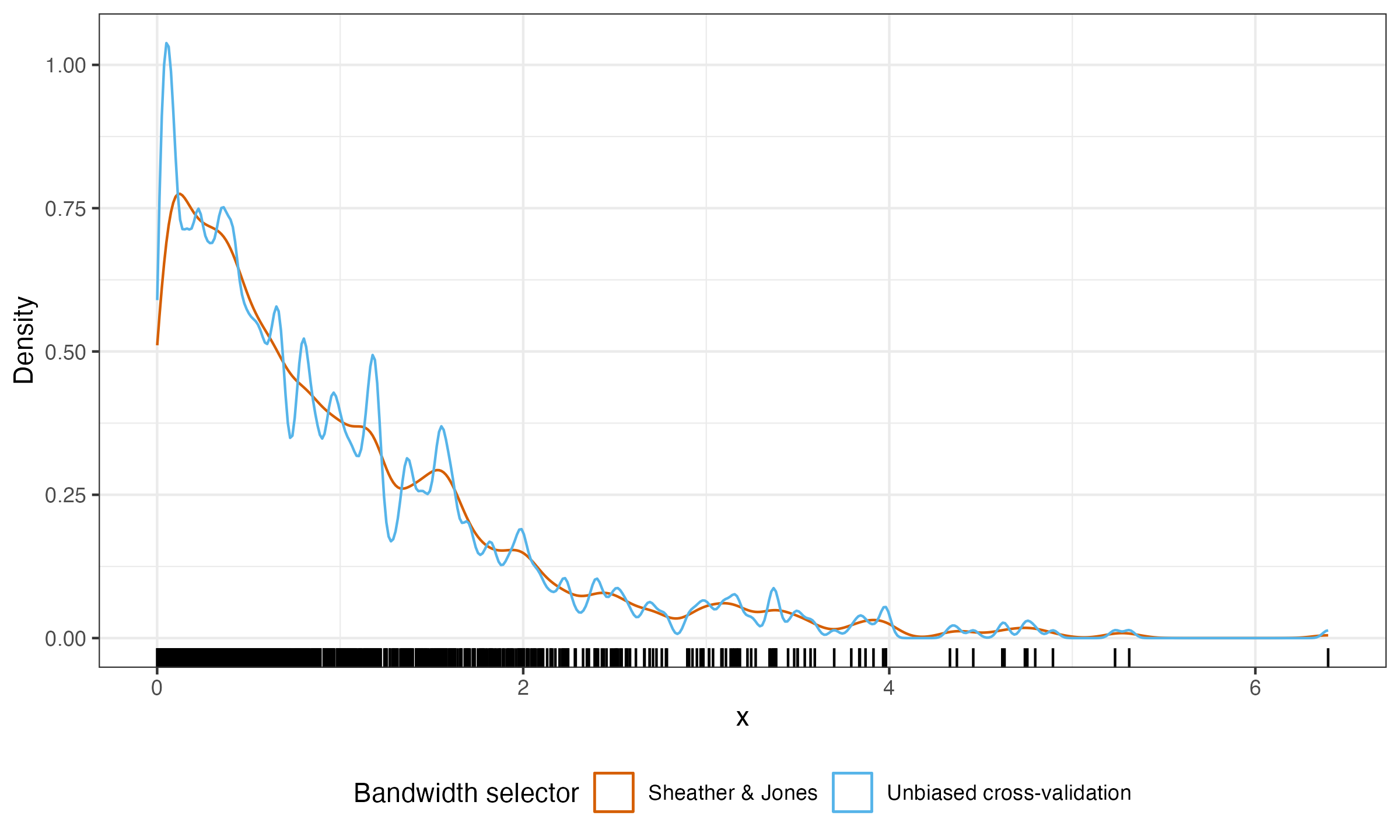
Now let us consider a random sample of size 1000 from the standard exponential distribution. Here is the KDE for this sample based on the Sheather & Jones and unbiased cross-validation bandwidth selectors:

As we can see, unbiased cross-validation gives us a wobbly line that is obviously overfitted to the data. Meanwhile, the Sheather & Jones method provides a much smoother plot.

Conclusion

The Sheather & Jones method is still one of my favorite KDE bandwidth selectors. In most cases, it correctly highlights multimodality, unlike Scott’s rule of thumb, Silverman’s rule of thumb, and the biased cross-validation method. However, it is not so overfitted to data as the unbiased cross-validation method.