Sporadic noise problem in change point detection

We consider a problem of change point detection at the end of a time series. Let us say that we systematically monitor readings of an indicator, and we want to react to noticeable changes in the measured values as fast as possible. When there are no changes in the underlying distribution, any alerts about detected change points should be considered false positives. Typically, in such problems, we consider the i.i.d. assumption that claims that in the absence of change points, all the measurements are independent and identically distributed. Such an assumption significantly simplifies the mathematical model, but unfortunately, it is rarely fully satisfied in real life. If we want to build a reliable change point detection system, it is important to be aware of possible real-life artifacts that introduce deviations from the declared model. In this problem, I discuss the problem of the sporadic noise.

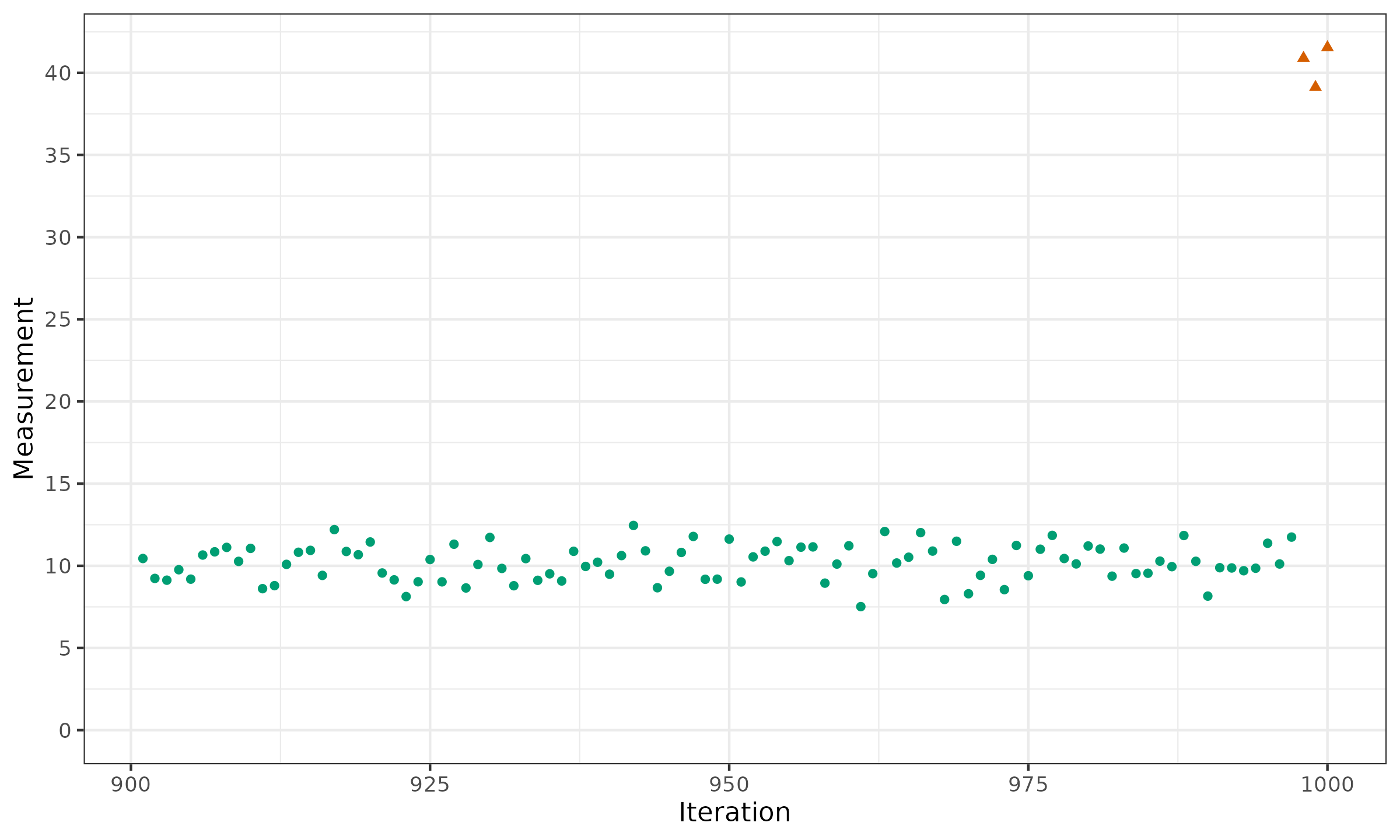
Let us look at the following time series consisting of 100 measurements:

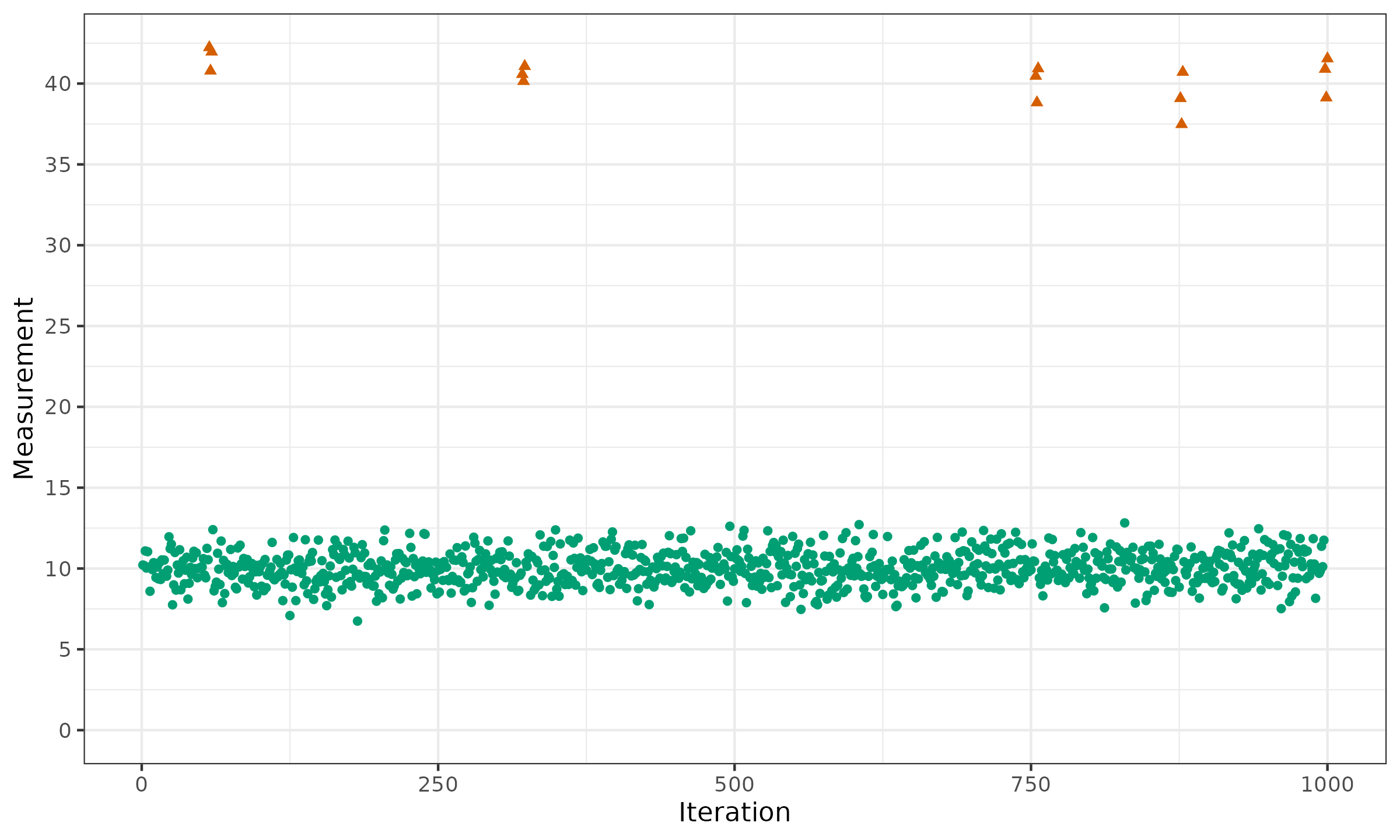
From the first look, we may assume an obvious change point at the end. Indeed, the first 97 measurements fit the interval $[5;15]$, but the last three measurements are around $40$. Should we react to such a change? Before we provide the conclusion, let us extend the time series to the past and explore the last 1000 measurements:

Here, we can see a pattern: in some random places, the time series contains a group of three extreme outliers. In the above picture, we have five such groups: $(57,58,59)$; $(321,322,323)$; $(754,755,556)$; $(876,877,878)$; $(998,999,1000)$. But these are not usual outliers! If the underlying distribution is a heavy-tailed one, we should expect occasional outliers. However, under the i.i.d. assumption, the outliers are expected to be more “uniformly distributed.” A proper robust change point detector should correctly handle such occasional outliers.

When we discuss sporadic outliers under deviations from the i.i.d. assumptions, we assume that such exceptional values occur at irregular intervals and are not representative of a true shift in the underlying process. The occurrence of these sporadic outliers can often be attributed to external factors beyond our control. These may include environmental changes, equipment malfunctions, or even data recording errors. For example, a sudden spike in temperature readings could be a result of a temporary environmental anomaly or a malfunctioning sensor, rather than a genuine climatic shift. It is crucial to differentiate these anomalies from genuine change points to avoid false alarms.

To effectively handle sporadic noise in change point detection, it is essential to incorporate robust methods that can distinguish between true distributional changes and random noise. However, it’s also important to acknowledge the limitations of these techniques. No method can perfectly filter out all noise, especially when dealing with complex real-world data. The key is to strike a balance between sensitivity to genuine changes and resilience to sporadic noise. This often involves fine-tuning parameters and thresholds based on the specific characteristics of the data and the context of the problem.