Statistical Efficiency of the Tau Measure of Location

For a sample $\mathbf{x} = (x_1, x_2, \ldots, x_n)$, the tau measure of location is defined as follows (described in Introduction to Robust Estimation and Hypothesis Testing, Edition 5, Section 3.8.1):

$$ \hat{\mu}_{\tau}(\mathbf{x}) = \left( \sum_{i=1}^n w_i x_i \right) / \left( \sum_{i=1}^n w_i \right), $$

where

$$ w_i(\mathbf{x}) = W_c \left( \frac{x_i - \operatorname{median}(\mathbf{x})}{\operatorname{MAD}(\mathbf{x})} \right), \quad W_c(x) = \left( 1 - (x/c)^2 \right)^2 \cdot I(|x| \leq c), $$

where $I$ is the indicator function, $\operatorname{MAD}$ is the median absolute deviation, $\operatorname{median}$ is the sample median, and $c$ is a constant (the proposed default value is 4.5).

In this post, we briefly check out the statistical efficiency of this measure compared to the mean, the median, and Hodges-Lehmann Estimator.

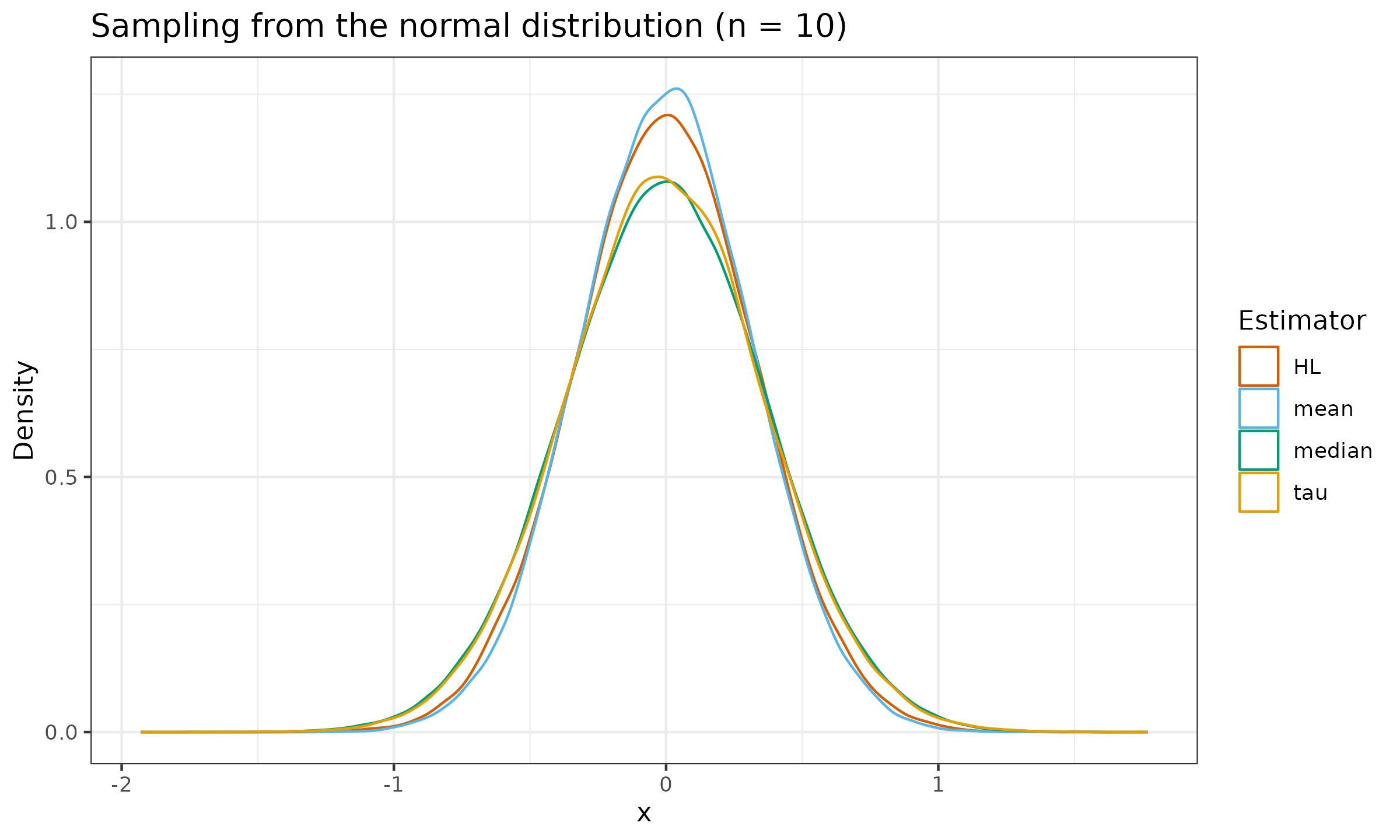
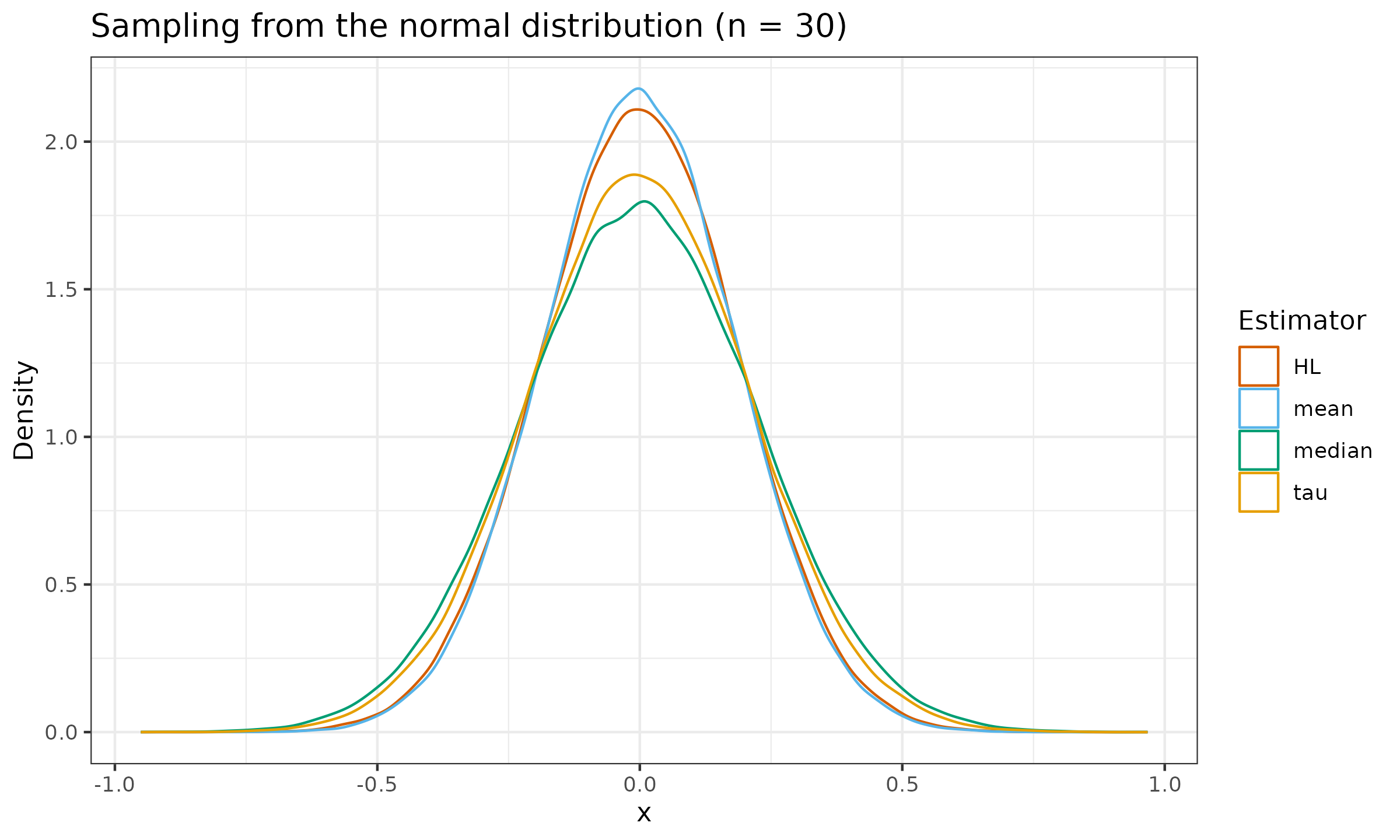
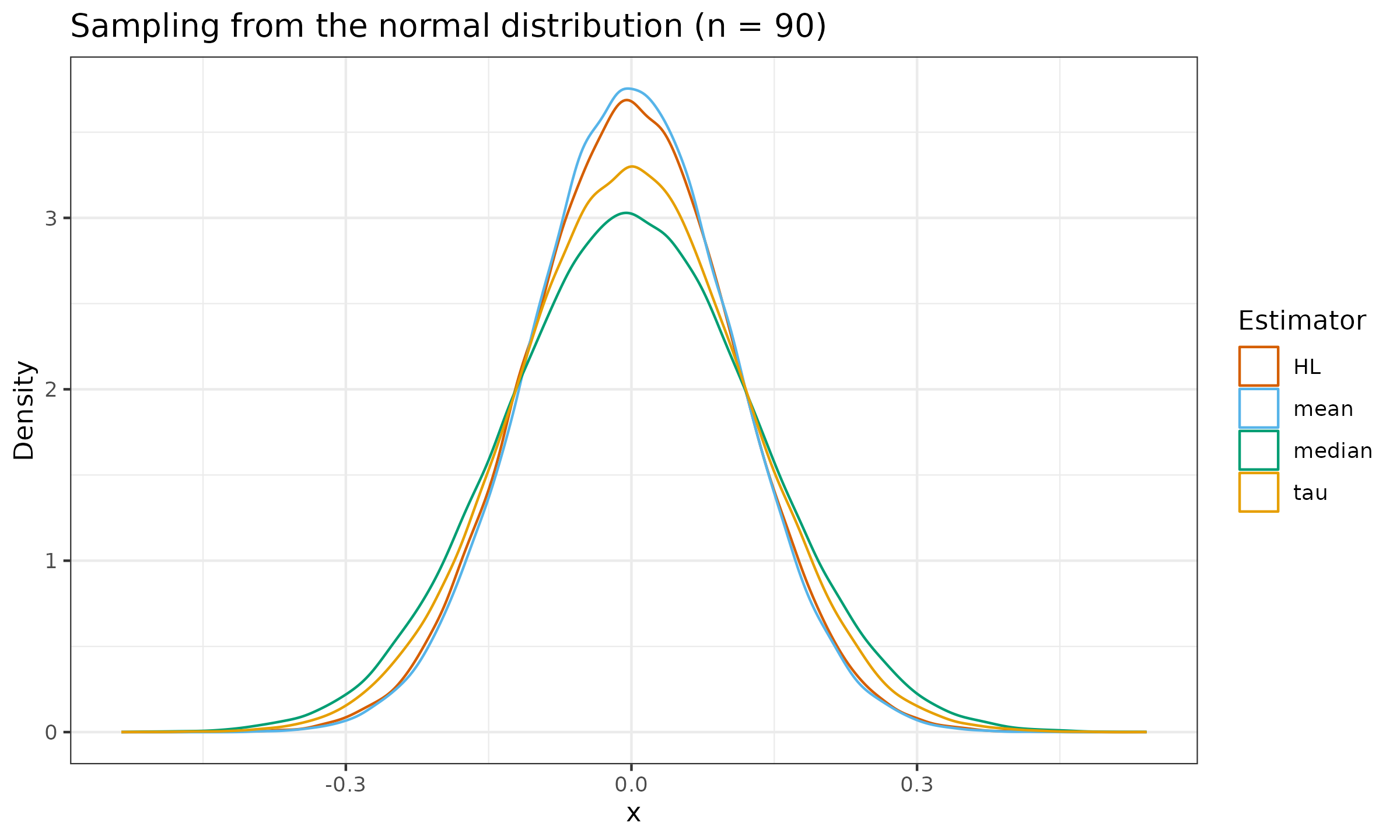
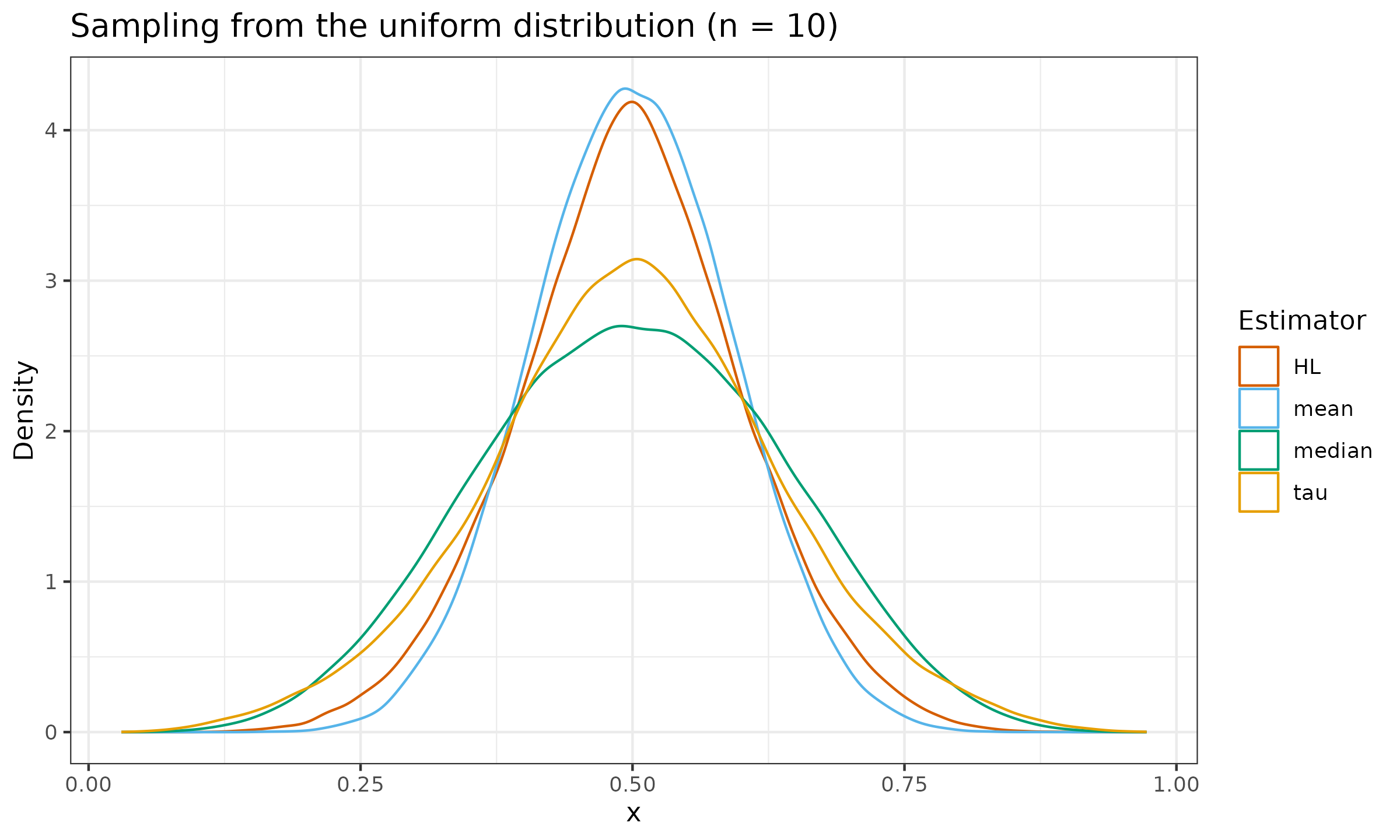
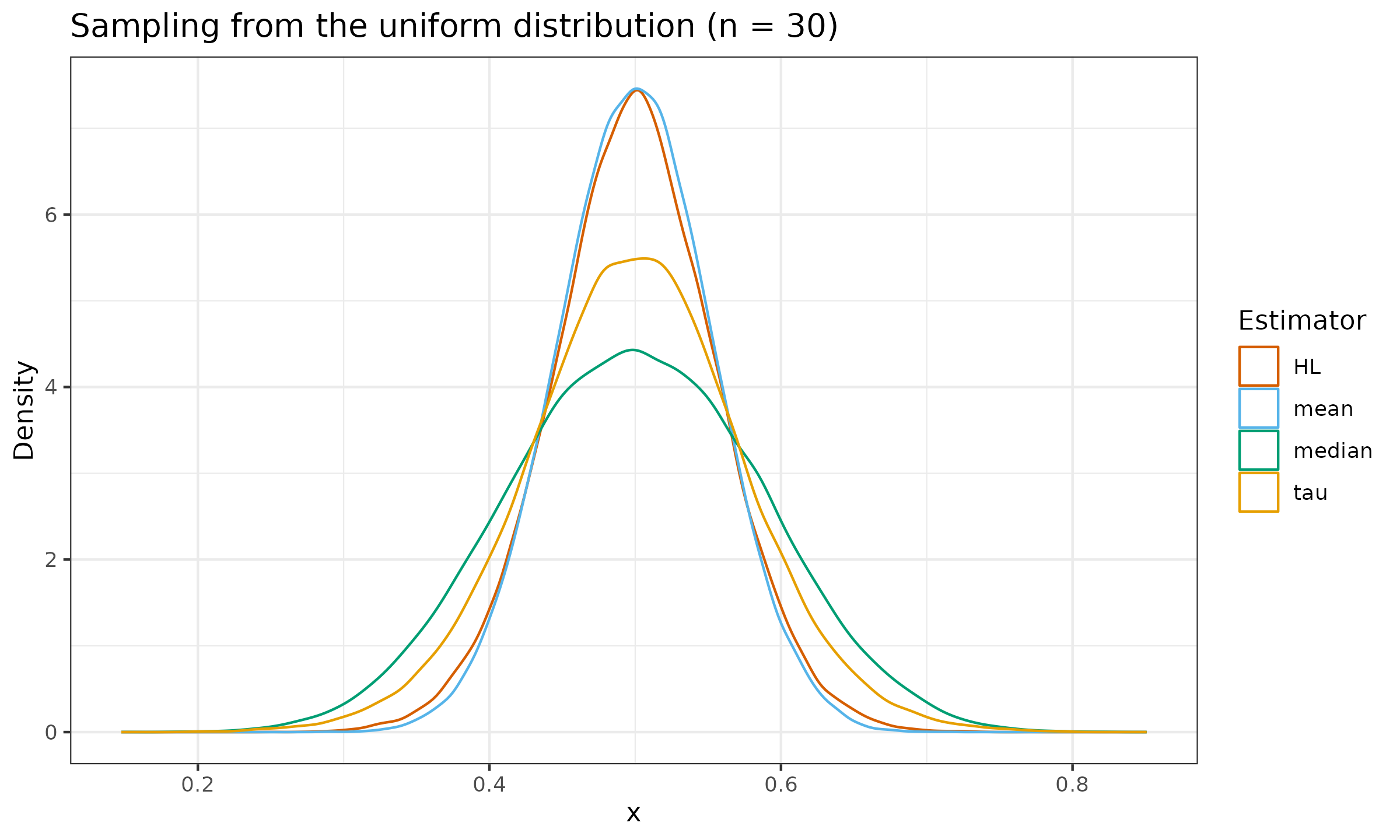
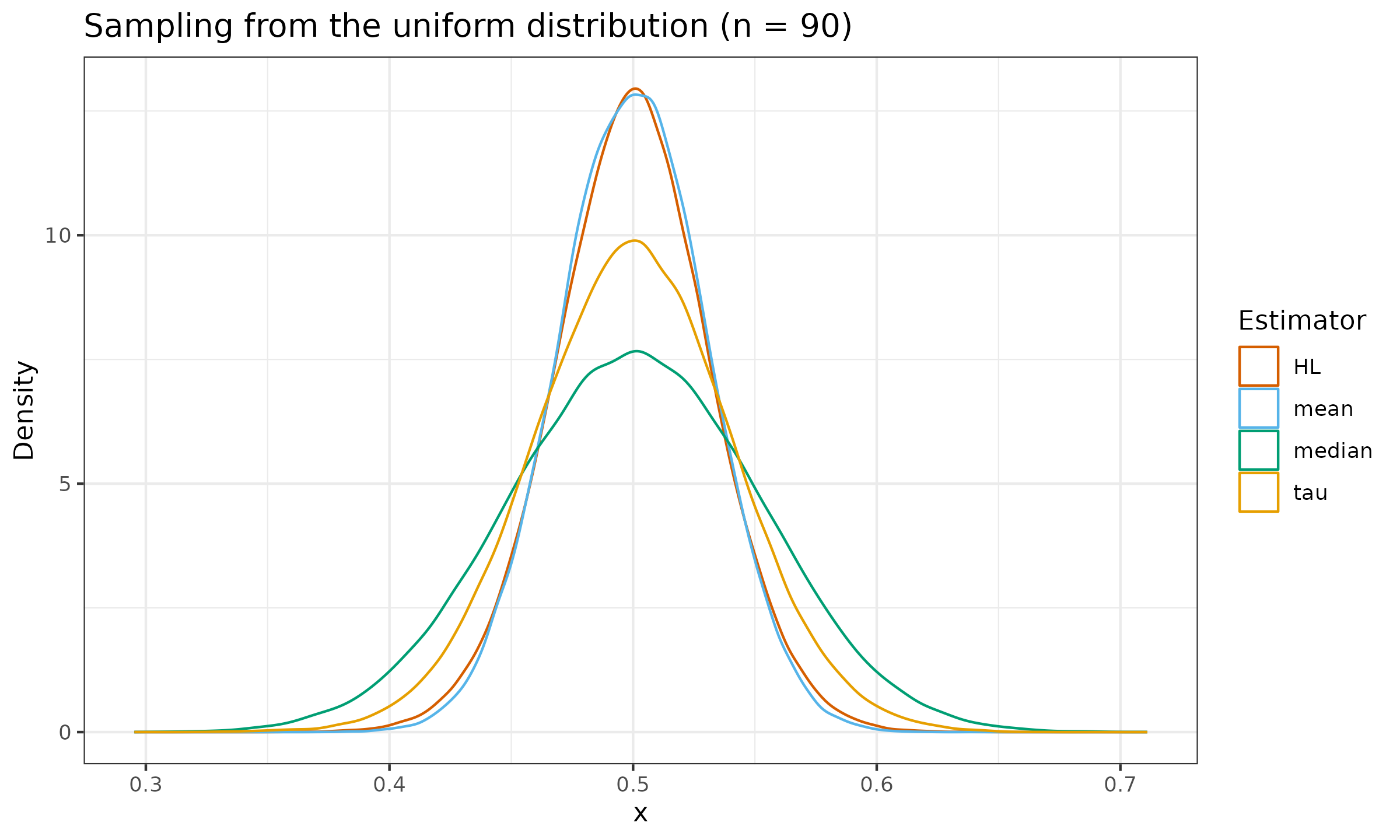
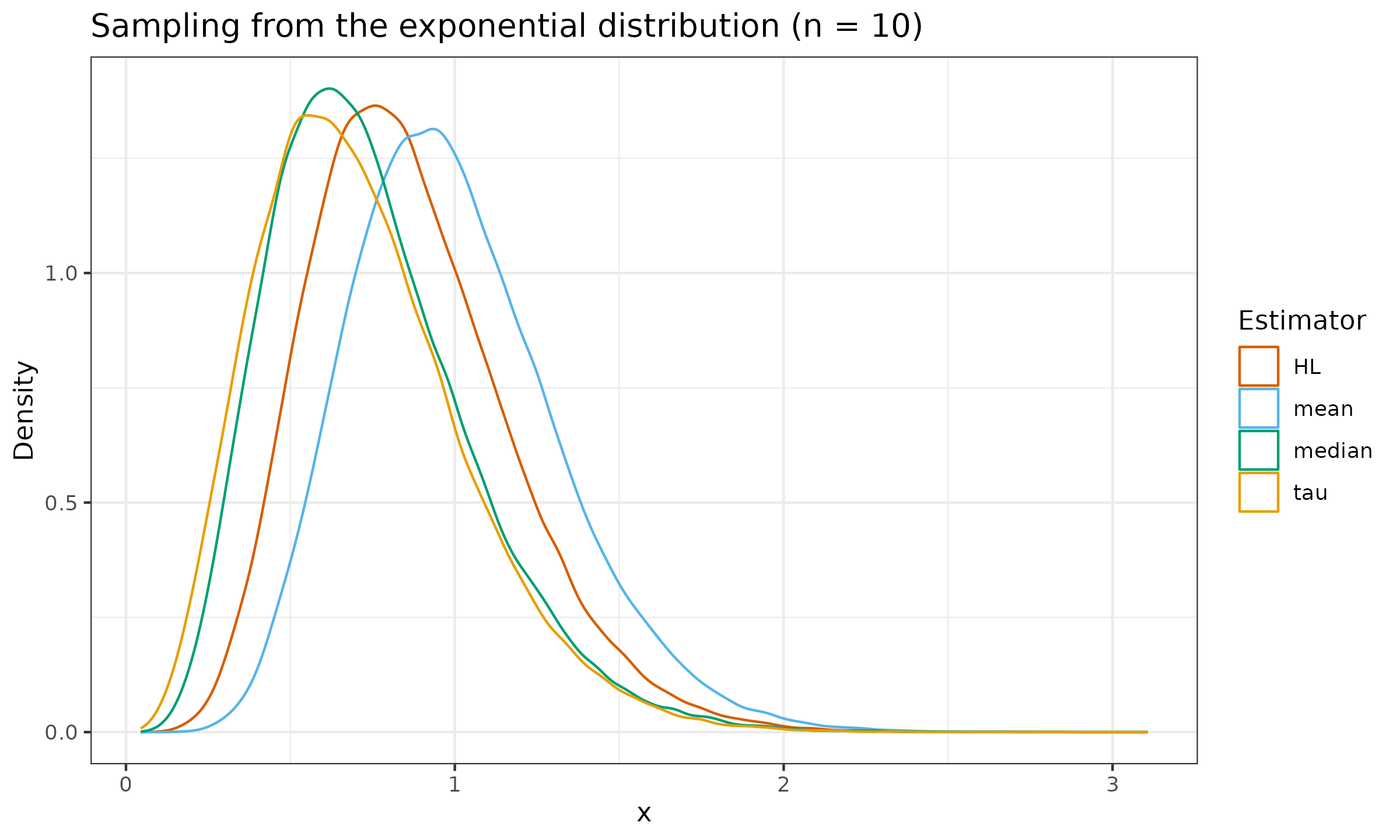
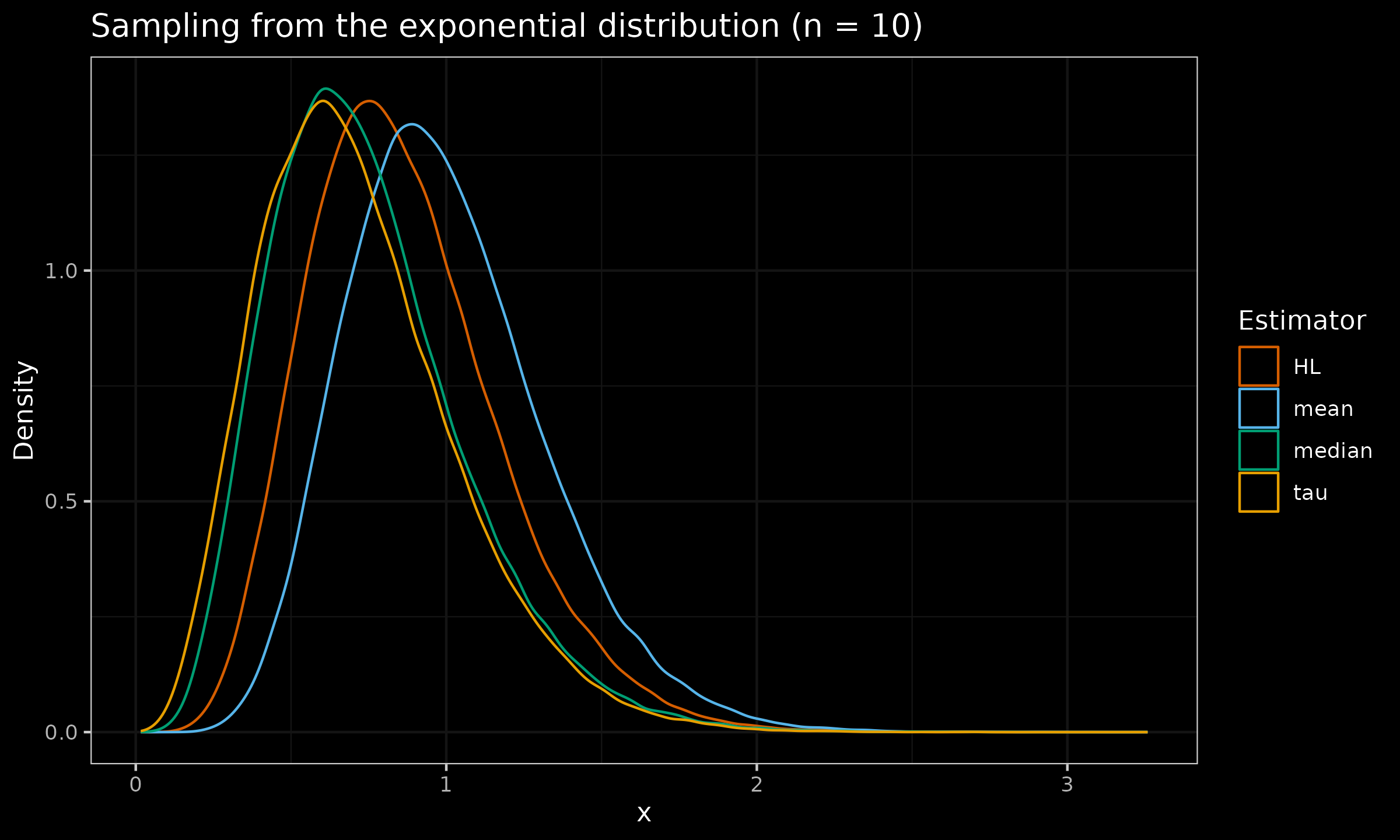
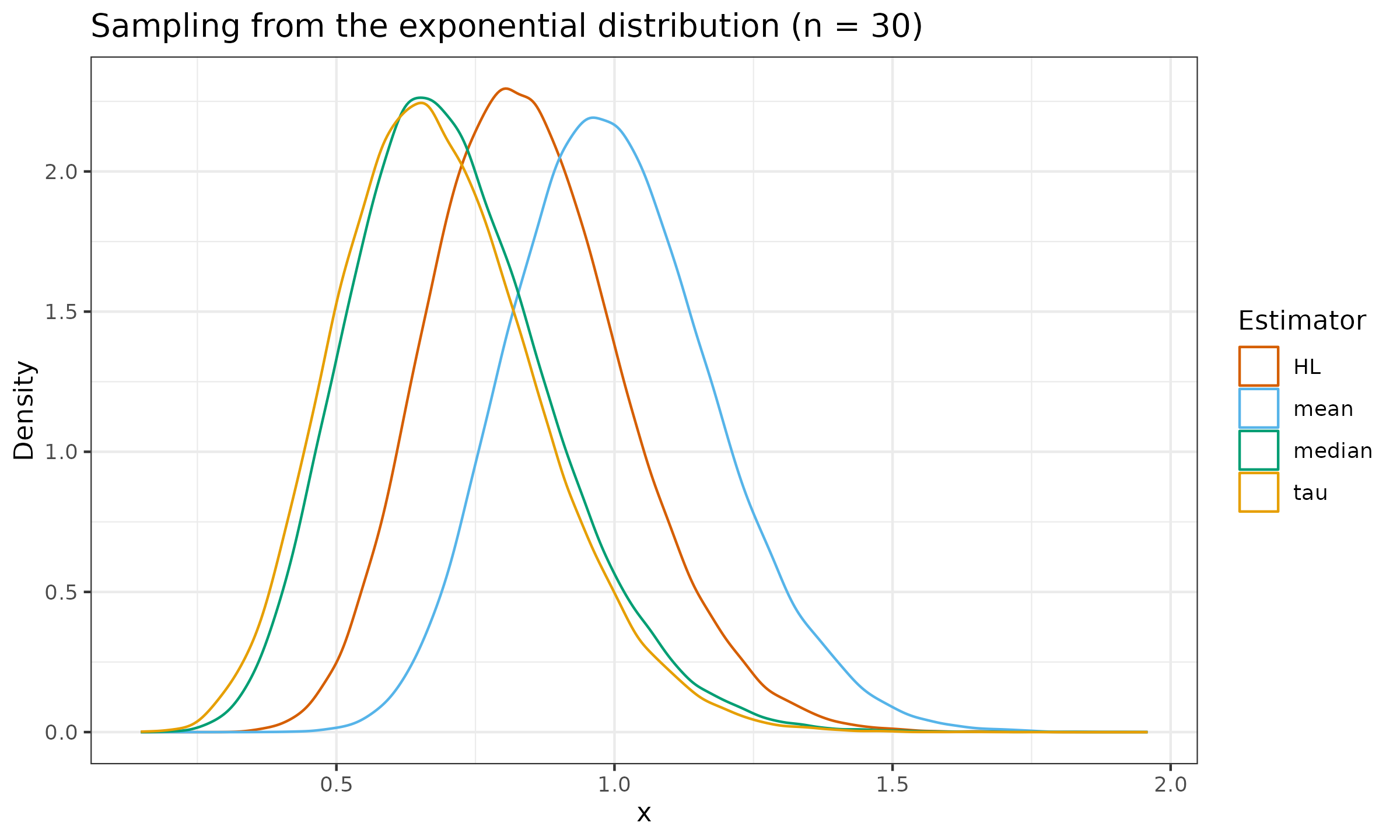
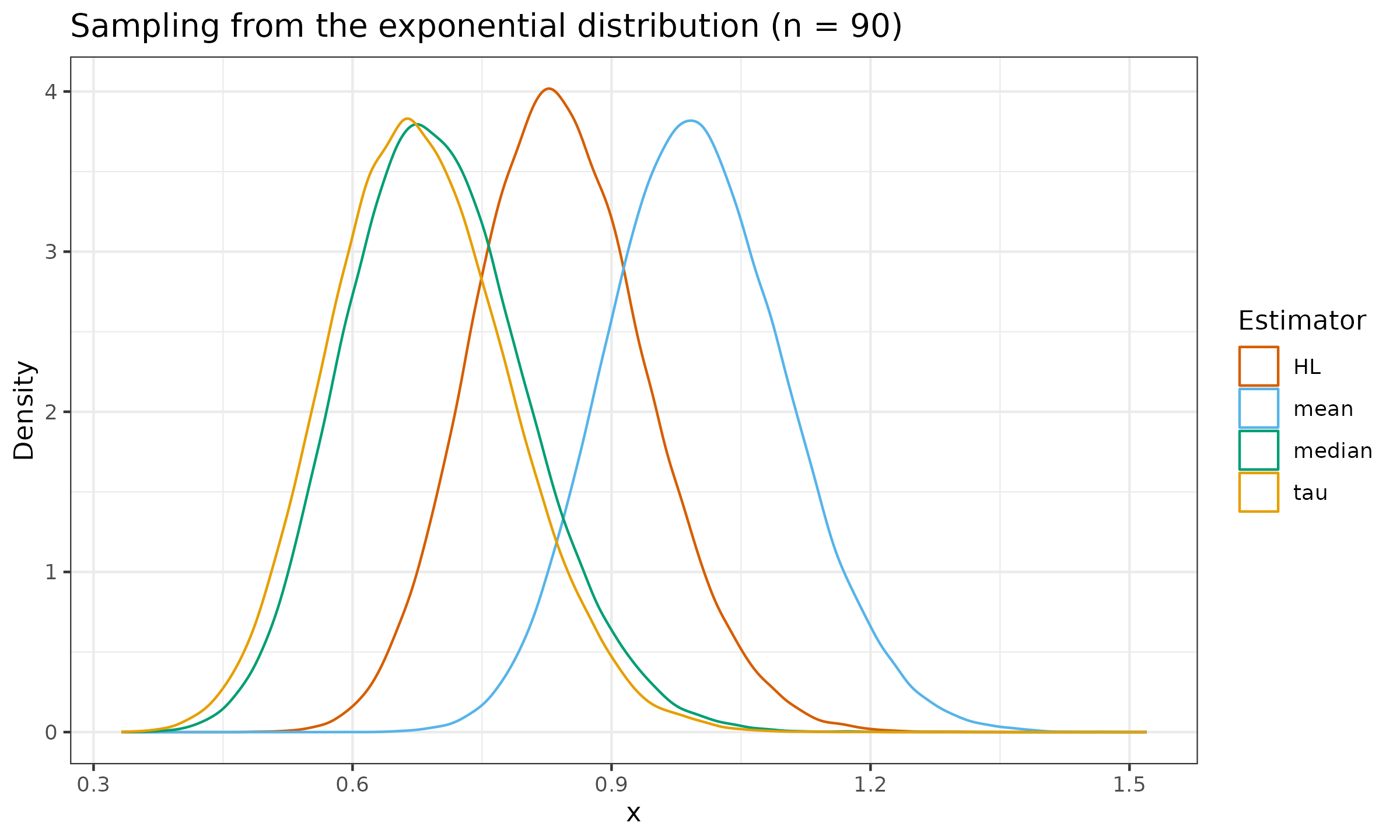
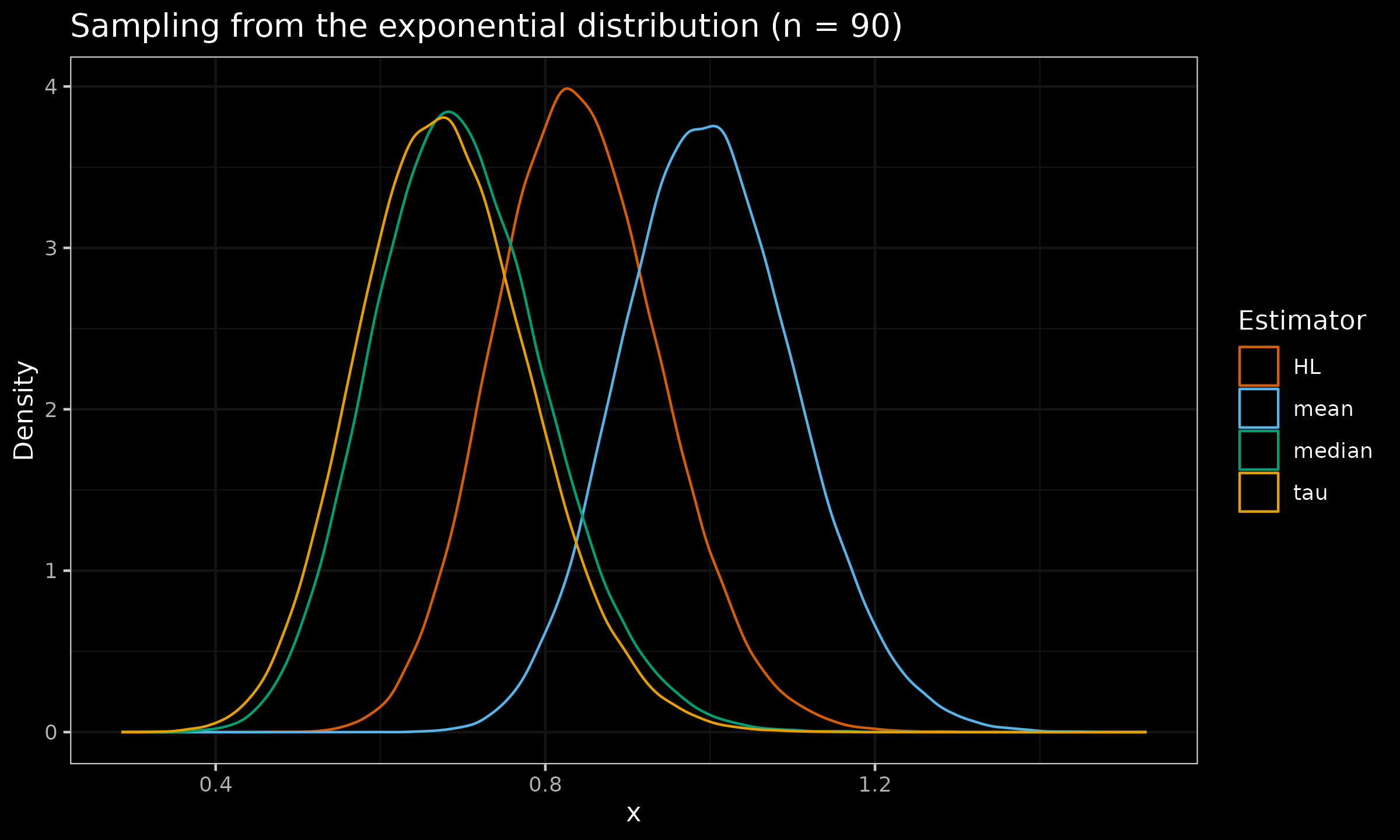
Let us evaluate the sampling distribution from the standard normal distribution $\mathcal{N}(0, 1)$, the standard uniform distribution $\mathcal{U}(0, 1)$, and the standard exponential distribution $\operatorname{Exp}(1)$ for $n \in \{ 10, 30, 90 \}$:

As we can see, the tau measure of location is slightly more efficient than the median, but it still lags behind the Hodges-Lehmann estimator.