Finite-sample Gaussian efficiency of the trimmed Harrell-Davis median estimator

In the previous post, we obtained the finite-sample Gaussian efficiency values of the sample median and the Harrell-Davis median. In this post, we extended these results and get the finite-sample Gaussian efficiency values of the trimmed Harrell-Davis median estimator based on the highest density interval of the width $1/\sqrt{n}$.

Similarly to the previous experiment, I have conducted a numerical simulation which enumerates various sample sizes (2..100); generates 1,000,000 samples from the normal distribution; estimates the mean, the sample median (SM), the Harrell-Davis median for these samples (HD), and the trimmed Harrell-Davis median based on the highest density interval of size $1/\sqrt{n}$ (THD-SQRT); calculates the finite-sample relative efficiency of the sample median and the Harrell-Davis median to the mean (the Gaussian efficiency). 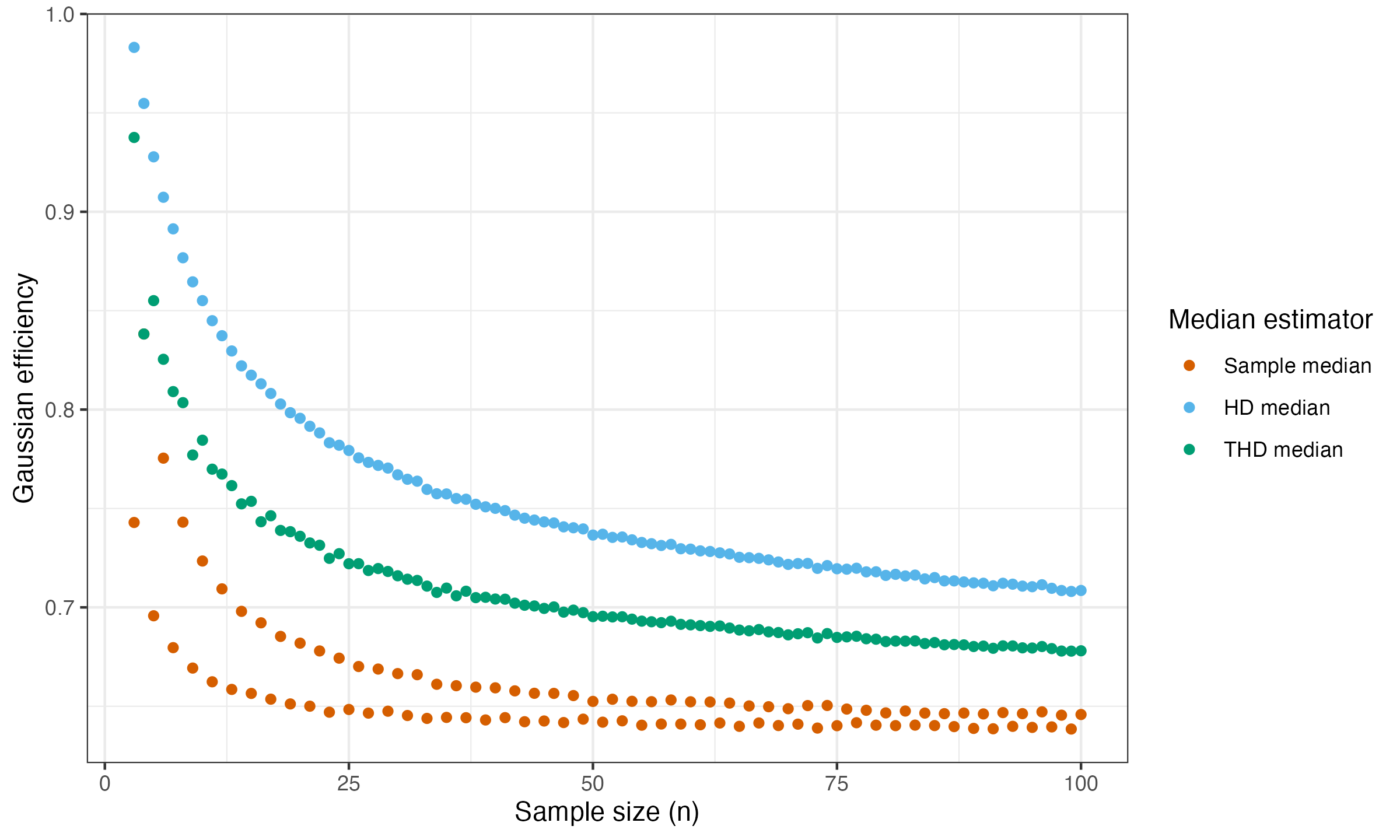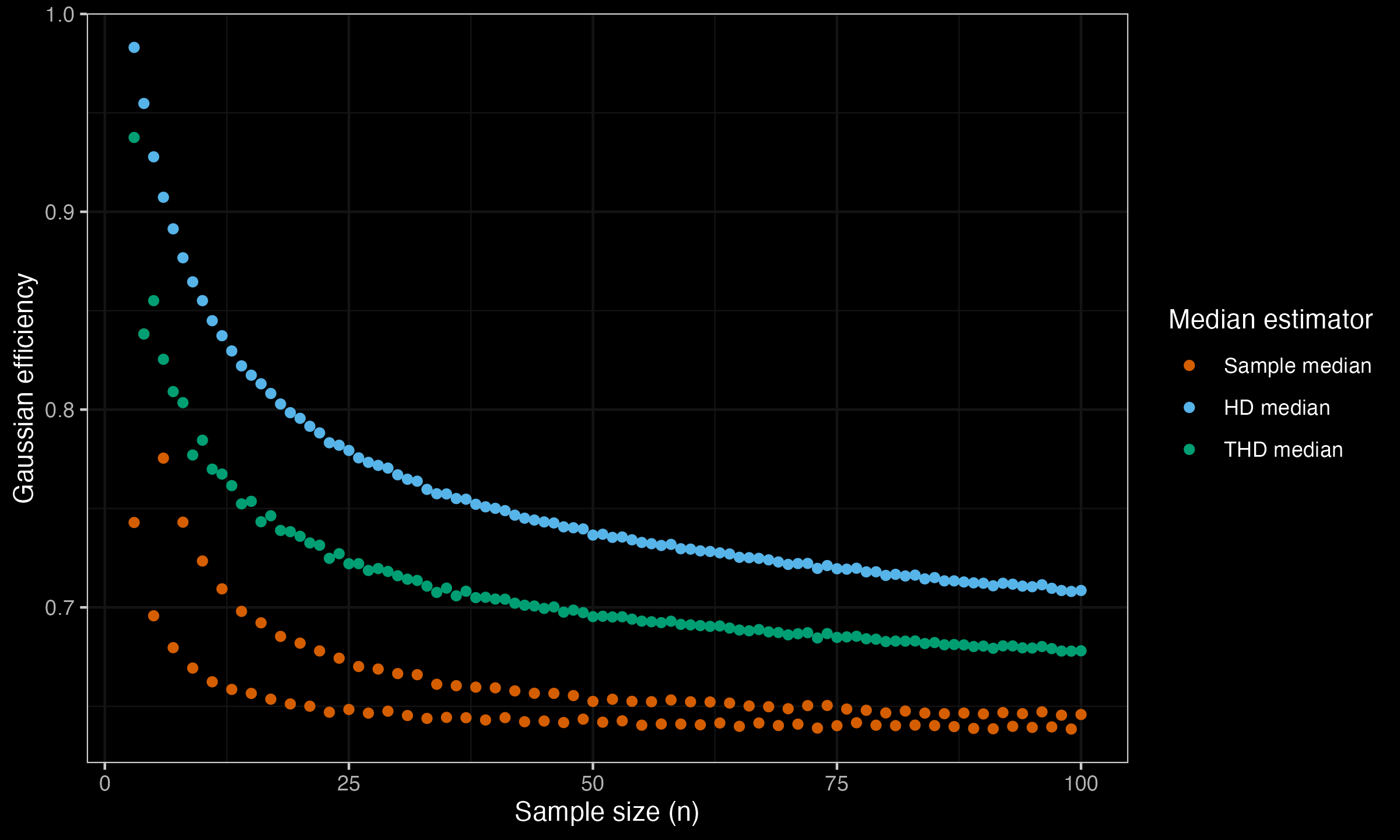Here are the results:

As we can see, THD-SQRT is less efficient than HD (which is the price of robustness), but it is still more efficient than SM.