Weighted modification of the Hodges-Lehmann location estimator

The classic Hodges-Lehmann location estimator is a robust, non-parametric statistic used as a measure of the central tendency. For a sample $\mathbf{x} = \{ x_1, x_2, \ldots, x_n \}$, it is defined as follows:

$$ \operatorname{HL}(\mathbf{x}) = \underset{1 \leq i < j \leq n}{\operatorname{median}} \left(\frac{x_i + x_j}{2} \right). $$

This estimator works great for non-weighted samples (its asymptotic Gaussian efficiency is $\approx 96\%$, and its asymptotic breakdown point is $\approx 29\%$). However, in real-world applications, data points may have varying importance or relevance. For example, in finance, different stocks may have different market capitalizations, which can impact the overall performance of an index. In social science research, survey responses may be weighted based on demographic representation to ensure that the final results are more generalizable. In software performance measurements, the observations may be collected from different source code revisions, some of which may be obsolete. In these cases, the classic $\operatorname{HL}$-measure is not suitable, as it treats each data point equally.

We can overcome this problem using weighted samples to obtain more accurate and meaningful central tendency estimates. Unfortunately, there is no well-established definition of the weighted Hodges-Lehmann location estimator. In this blog post, we introduce such a definition so that we can apply this estimator to weighted samples keeping it compatible with the original version.

Proposed definition

Let us consider a vector of weights $\mathbf{w} = \{w_1, w_2, \ldots, w_n \}$, $w_i$ describes the weight of $x_i$. We propose the following definition for the weighted Hodges-Lehmann location estimator:

$$ \operatorname{WHL}(\mathbf{x}, \mathbf{w}) = \underset{1 \leq i < j \leq n}{\operatorname{median}} \left(\frac{x_i + x_j}{2};\;\; w_i \cdot w_j \right). $$

This estimation uses the weighted median of the pairwise averages $(x_i+x_j)/2$ with weight coefficients given by the products of the corresponding element weights $w_i \cdot w_j$. This approach ensures that we acknowledge each observation’s importance during the calculation.

Numerical simulation

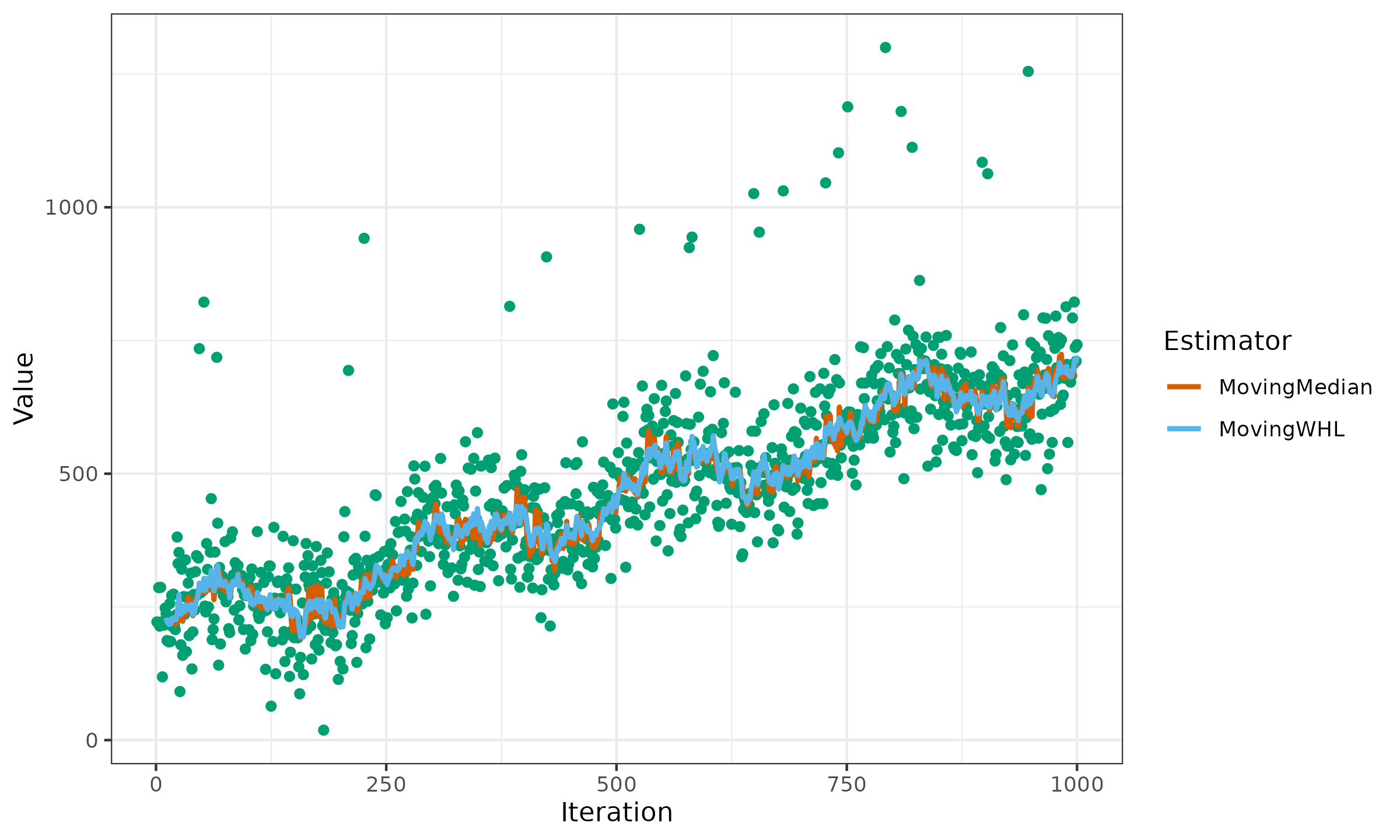
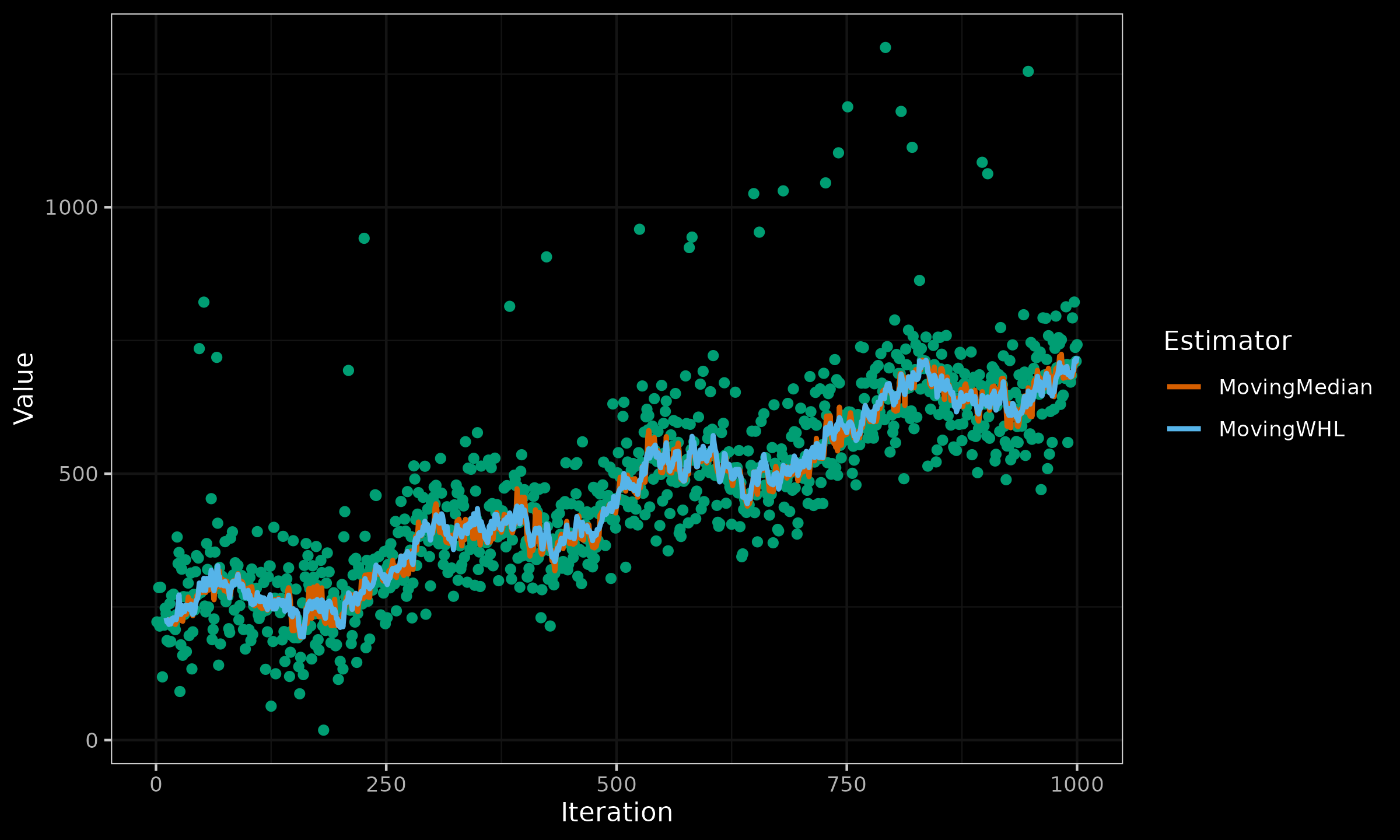
Now we conduct a numerical simulation to explore the new estimator in action. We consider the problem of moving central tendency estimation using exponential smoothing (half-life value is 5 data points). For the time series, we consider a monotonically increasing noisy sine wave pattern with extreme outliers. For the estimators, we consider the weighted median and the discussed weighted Hodges-Lehmann location estimator. Here are the results:

As we can see, the moving weighted Hodges-Lehmann location estimator performs approximately the same as the moving weighted median.

Conclusion

The weighted Hodges-Lehmann location estimator introduced in this blog post can be useful in various applications where data points have different importance or reliability. As previously mentioned, we have presented only one way to define the weighted Hodges-Lehmann location estimator, while other approaches can also be considered. It is crucial for researchers to evaluate the suitability of the suggested definition or any other methods within their specific context, taking into account the characteristics of the data and the business requirements.

References

• [Hodges1963]
  Hodges, J. L., and E. L. Lehmann. “Estimates of Location Based on Rank Tests.” The Annals of Mathematical Statistics 34, no. 2 (June 1963): 598–611.
  https://doi.org/10.1214/aoms/1177704172.